卫星控制力矩陀螺微振动抑制装置的动力学建模与实验研究

王嘉登， 张高雄， 茅 敏， 陆国平， 刘兴天

(上海卫星工程研究所 空间机热一体化技术实验室，上海 201109)

随着航天科技的快速发展，高分辨率光学遥感卫星在国民生活和国防事业中发挥着越来越重要的作用，其搭载的光学载荷对卫星姿态控制稳定度以及微振动环境有了更苛刻的要求。作为很多航天器姿态控制系统的主要执行机构[1-3]，控制力矩陀螺(CMG)在轨工作时，转子一直处于高速旋转状态，由于动不平衡、轴承缺陷等因素，使其成为航天器上微振动主要来源之一[4-5]。为了给航天器有效载荷提供超静工作环境，有必要对CMG产生的振动进行抑制[6]。目前抑制此类微振动的有效措施是进行振源隔离[7-10]。

国内外学者在微振动抑制领域进行了大量研究。哈勃望远镜中使用Honeywell公司设计的黏性液体阻尼器来隔离飞轮产生的扰动[11]；Cobb等[12]研制了一种用于太空光学望远镜的主、被动混合隔振平台；美国喷气推进实验室设计了一种柔性主动隔振平台，并成功应用于詹姆斯韦伯太空望远镜[13]。Stewart平台因其具有自由度大，设计简单等优势，被广泛用于主、被动隔振平台，来抑制航天器在轨微振动[14]。众多学者对Stewart隔振平台基本特性进行了深入研究。杨剑锋[15]推导了被动式Stewart隔振平台的动力学方程，分析了隔振平台在基础位移激励下的隔振性能。吴国军[16]使用Kane方法建立了带有柔性悬臂梁的Stewart隔振平台的非线性动力学方程，分析了隔振系统上平台质心处的动响应。张尧等[17]研究了用于控制力矩陀螺群的隔振平台，该隔振平台通过在典型隔振平台基础上添加调谐质量阻尼器实现了主动隔振效果。何兆麒等[18]在考虑支腿绕自身轴线的旋转自由度的基础上，建立了完善的牛顿-欧拉闭环动力学模型。

虽然针对Stewart隔振平台的研究较多，但大多基于Kevin隔振模型或主要研究主动控制算法，而对松弛型阻尼Stewart隔振平台的研究较少，且未能建立准确的隔振性能评价标准。

本文提出基于松弛型阻尼器的Stewart隔振平台，采用“立方体”构型，单个隔振单元使用松弛型阻尼器[19-20]，获取了共振大阻尼。高频小阻尼，具有良好共振峰抑制和高频衰减效果的隔振装置，满足控制力矩陀螺的使用要求。首先，运用牛顿-欧拉法建立了隔振平台的动力学模型；随后，分析了隔振平台的频率特性、隔振性能以及耦合特性；最后，搭建实验平台进行了隔振实验，验证了理论的正确性。

1 动力学特性

1.1 系统介绍

微振动抑制装置如图 1所示，装置由上、下平台和六个支腿组成，每个支腿为一个松弛型阻尼器。将微振动抑制装置简化为图 2所示的模型，每个支腿为弹簧和阻尼组成的单元。定义上平台局部坐标系、下平台局部坐标系和全局惯性坐标系分别为Pxpypzp、Bxbybzb和Gxyz；铰链与上、下平台连接的坐标系分别为Pixpiypizpi和Bixbiybizbi；控制力矩陀螺惯量主轴坐标系为Oxyz。

图1 微振动抑制装置的三维模型图

以下符号被用于系统建模中：tp为上平台质心在G系中的位置矢量；pi为上平台各铰点在P系中的位置矢量，bi为下平台各铰点在B系中的位置矢量；ti为各支腿在G系下的矢量；R0为上平台和质量负载的综合质心在P系中的位置矢量；ωp、αp为上平台角速度、角加速度；ωb、αb为下平台角速度、角加速度；Ip为上平台和控制力矩陀螺在G系中的惯量矩阵；Iu0i、Id0i为上、下支腿相对于质心分别在Pi系、Bi系中的惯量矩阵；ru0i、rd0i为上、下支腿质心分别在Pi系、Bi系中的位置矢量。

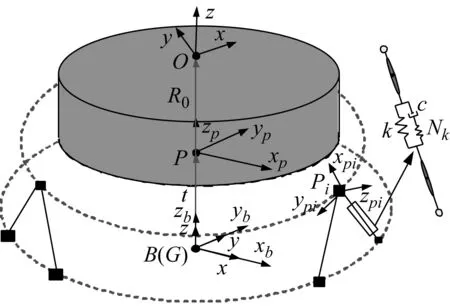
(a) 简化模型

(b) 俯视图

1.2 动力学建模

1.2.1 支腿动力学建模

众多学者考虑的支腿为弹簧阻尼单元的Kevin模型，本文中，采用松弛型阻尼器代替传统的弹簧阻尼单元，支腿的模型和受力分析如图 3所示。由Stewart平台的对称性，可得第i条支腿在{G}系下的位置矢量li为

li=Pi-Bi=tpi+tp-tbi-tb

(1)

式中：tpi=Rp，gpi，tbi=Rb，gbi，tp=[0 0h]T，tb=[0 0 0]T。

图3 第i条支腿受力分析图

第i条支腿沿支腿方向的单位矢量可写成

τi=li/|li|

(2)

第i条支腿滑动速度和滑动加速度分别为

(3)

api=api+u1i

(4)

式中：u1i=ωp×(ωp×tpi)。

经计算可得上、下支腿质心处加速度表达式

(5)

(6)

式中：u4i=ωp×(ωp×tpi)+ωi×(ωi×rui)+u3i×rui，u5i=ωi×(ωi×rdi)+u3i×rdi。

对上、下支腿质心取矩的动量矩方程如下

(7)

(8)

化简可得整个支腿对上平台的约束力为

(9)

1.2.2 上平台动力学建模

如图4所示，设支腿作用于上平台的反作用力为-Fsi，上平台和控制力矩陀螺的综合重力为m0g，控制力矩陀螺引起的总扰动力和总扰动力矩分别为Fmac、Mmac。

图4 上平台受力简图

使用Newton-Euler法可得上平台动力学方程

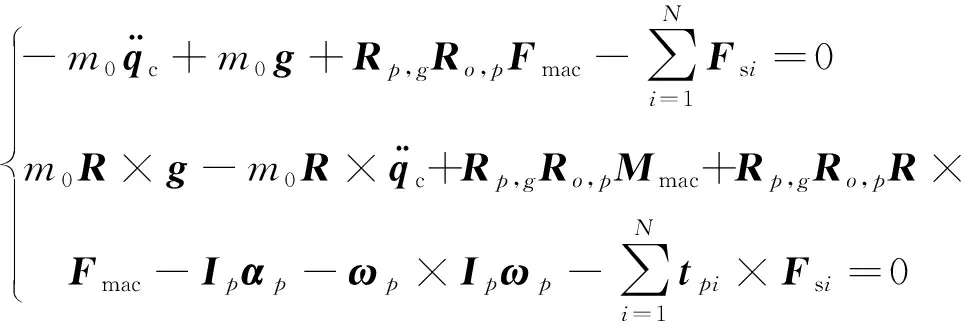
(10)

1.3 响应求解

上支腿作用在上平台的作用力Fi为

(11)

式中：xdi为第i条支腿阻尼单元和与其串联的弹簧单元中间连接点的压缩量。

对式(11)进行拉氏变换，化简得：

(12)

联立式(9)、式(10)和式(12)，得到隔振系统的动力学方程

(13)

其中

由此，给出微振动抑制装置的参数、基础激励、干扰力和干扰力矩，代入式(13)，可得微振动抑制装置上平台的响应。

2 微振动抑制装置性能分析

本文使用传递率表示微振动抑制装置的隔振性能，定义传递率为传递至上平台的加速度响应幅值与基础激励幅值的比。装置的基本参数根据控制力矩陀螺进行设计，其中，控制力矩陀螺和微振动抑制装置主要参数实测得到，松弛型阻尼器刚度和阻尼选择适当的数值，主要参数如表1～表3所示。

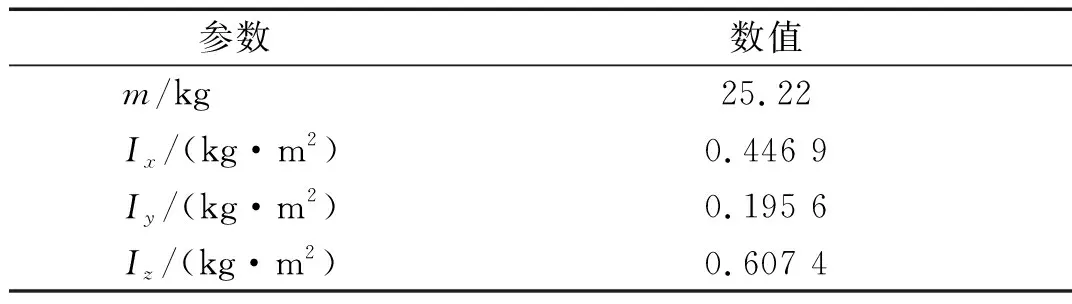
表1 控制力矩陀螺主要参数

2.1 固有频率分析

首先对系统的固有特性进行分析。固有频率只与系统本身属性有关，而与外界激励无关，因此，对动力学方程(13)进行化简，得到无阻尼系统自由振动方程

表2 松弛型阻尼器主要参数

表3 微振动抑制装置结构参数

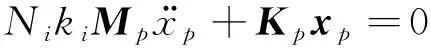
(14)

式中:Kp为系统的等效刚度矩阵;NikiMp为等效质量矩阵。求解式(14)得到系统的六阶固有频率总结在表4中，同时，得到系统的模态矩阵如表5所示。

表4 固有频率理论解

表5 隔振平台模态矩阵

从固有频率及模态矩阵可以看出，除第三阶为单纯沿Z轴的平移、第五阶为绕Z轴的扭转外，其余四阶均为扭转和质心平移的叠加，隔振系统的耦合主要在X和Y方向。

2.2 松弛型阻尼器隔振性能分析

不同于Kevin模型，松弛型阻尼器的隔振性能不仅受到阻尼因子的影响，还受到刚度比的影响。刚度比是松弛型阻尼器的重要参数，其不仅决定了共振峰的位置，而且和共振放大系数紧密相关。为比较松弛型阻尼器和Kevin模型的差异，将刚度比为4的松弛型阻尼器和参数为k=50 N/mm，c=800 N·s/m的Kevin模型的传递率画在同一副图中进行比较，此状态下，隔振系统在Z向的传递率曲线如图5所示。

图5 松弛型阻尼和Kevin模型加速度传递率曲线对比图

图5中给出了两种系统在共振峰值相同时的传递率曲线。可以看出，设计合适的刚度比，可以使基于松弛型阻尼器的隔振装置性能优于传统Kevin隔振系统，以控制力矩陀螺100 Hz主频衰减为例，Kevin模型衰减为-20.1 dB，而松弛型阻尼器衰减为-31.2 dB；松弛型阻尼器在高频处的衰减明显优于Kevin隔振系统。

2.3 耦合特性分析

控制力矩陀螺质心相对于上平台的高度是微振动抑制装置产生耦合的主要原因[21]。本节以安装高度为变量研究系统的耦合特性，选取h=40 mm和h=0 mm进行分析，不同激励下各方向的传递率曲线如图6和图7所示。

图6 h=0 mm时控制力矩陀螺响应图

由图6和图7可知，当控制力矩陀螺质心和隔振平台刚度中心重合时，隔振系统各向无耦合；当控制力矩陀螺质心和隔振平台刚度中心不重合时，隔振系统沿X轴平移方向和绕Y轴转动方向，沿Y轴平移方向和绕X轴转动方向存在耦合，激励同时激发系统的平移模态和旋转模态，传递率曲线出现两个峰值；隔振系统沿Z轴平移方向和绕Z轴旋转方向和其他六个方向不存在耦合，其传递率曲线只出现一个峰值。因此，在设计该系统时，应根据实际的隔振要求并结合控制力矩陀螺的激励特性，合理选择控制力矩陀螺质心和刚度中心的距离，获取最优微振动抑制性能。

图7 h=40 mm时控制力矩陀螺响应图

2.4 隔振性能分析

对微振动抑制装置下平台施加激励幅值30 mg，(g为重力加速度，数值为9.8 m/s2)，频率2～40 Hz加速度扫频激励来研究隔振系统的隔振性能。得到基础激励下的传递率如图8所示，微振动抑制装置在控制力矩陀螺主频处的六方向隔振效率和共振峰放大倍数总结在表6中。

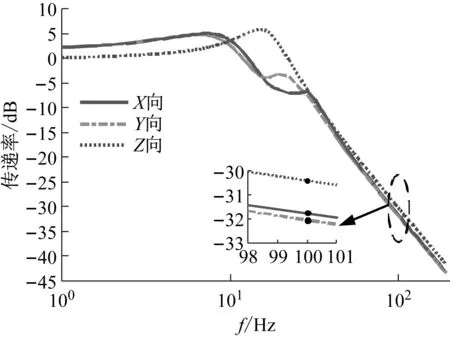
(a) 平移方向传递率

(b) 转动方向传递率

表6 微振动抑制装置六个方向的隔振性能

分析图8和表6可知，由于微振动抑制装置具有对称性，X和Y方向传递率曲线的固有频率基本相同；六个方向中，最小的固有频率为6.84 Hz(Y平移方向)，最大的固有频率为28.65 Hz(绕Y旋转方向)。隔振系统对控制力矩陀螺100 Hz主频振动处平移方向衰减均超过30 dB，隔振效率大于94%，且在共振频率附近放大不超过3倍。

3 隔振实验

本节搭建微振动抑制装置实验平台，通过对下平台施加正弦扫频激励，测量上平台加速度响应，验证装置的隔振性能。

3.1 实验方案

实验系统组成如图9所示，主要包括：微振动激励台、微振动抑制装置、加速度传感器、LMS数据采集系统和悬吊系统。

图9 实验测试系统

在控制力矩陀螺悬吊状态下(图10)，通过振动台输入正弦扫频激励信号，通过加速度传感器测量并记录上平台质心处的加速度变化情况，获取微振动抑制装置垂直方向的绝对加速度传递率。

图10 悬吊状态实验图

3.2 实验结果

振动台输入幅值为30 mg，频率范围为2～200 Hz的正弦扫频激励信号，上平台和CMG质心处加速度变化曲线如图11所示。同时，通过数据采集软件对时域信号进行处理，得到微振动抑制装置的传递率曲线如图12所示，为对比方便，图中同时给出了1.3节中的理论曲线以及Kevin模型的传递率曲线。

图11 Z向加速度响应曲线

图12 Z向隔振系统传递率曲线

从图11中可以看出，垂直激励时时域曲线出现一个峰值，与其他方向无耦合。从图12中可以看出，隔振系统对控制力矩陀螺100 Hz主频振动处振动衰减超过30 dB，且在共振频率附近放大不超过10 dB。实验结果表明：隔振平台对控制力矩陀螺产生的振动具有良好的衰减作用；共振峰值对应的横坐标为14.42 Hz，与求得的固有频率理论值相近；实验值和理论值吻合非常好，从而通过实验再次证明了理论模型的准确性。

3.3 激励幅值对传递率的影响

为了验证激励幅值对微振动抑制装置隔振性能的影响，实验中对隔振平台沿Z平移方向施加激励幅值分别为10 mg、20 mg和30 mg的激振力，所得传递率曲线如图13所示。可以看出，在不同幅值的激振力作用下，隔振系统的加速度曲线基本重合，表明激励幅值对隔振系统的隔振性能没有影响。

图13 不同激励幅值下沿Z平移方向加速度传递率曲线

4 结 论

本文基于松弛型阻尼器和立方体构型设计了卫星控制力矩陀螺微振动抑制装置，并进行了理论分析和实验研究。使用牛顿-欧拉法建立了系统的动力学方程，得到系统的六阶固有频率和模态矩阵，分析了抑制装置的耦合特性以及引起耦合振动的原因，结果表明，控制力矩陀螺质心相对于上平台的高度是微振动抑制装置产生耦合的主要原因，应结合控制力矩陀螺不同方向的干扰特性，合理选择设计参数。实验结果表明：微振动抑制装置对控制力矩陀螺100 Hz主频处的振动衰减超过30 dB，且在共振频率附近放大不超过10 dB，具有良好的隔振性能；激励幅值基本不会影响系统的隔振性能。本研究对卫星控制力矩陀螺在轨微振动抑制技术具有现实意义。