一种基于多测量向量模型的机械振动信号联合稀疏重构方法
2021-01-18郭俊锋
郭俊锋, 王 茁
(兰州理工大学 机电工程学院,兰州 730050)
机械振动现象广泛存在于机械设备中,机械振动信号承载并传递着机械设备运转过程中的多种信息,监测并提取振动过程中的有用信息,能帮助人们更好地掌握设备运行状态,及时进行维护。传统且被广泛采用的采样技术以奈奎斯特采样理论为基础,该定理要求:采样频率必须高于信号最高频率的两倍,否则原信号将不能被精确重构。近年来,大型设备的使用日趋多样,其运行过程也产生更加复杂的变化,如设备间隙、振动工况、摩擦、碰撞、频率的随机性等。机械设备所产生的数据也朝着“大数据”的方向发展,若此时仍采用传统的奈奎斯特采样定律进行采样,必然要求更高的采样频率,同时也会产生巨量的监测数据,而这些数据的传输、存储等问题已成为亟待解决的瓶颈问题[1]。
近年来压缩感知理论[2]的出现较好地解决了上述问题,该理论能以远远小于奈奎斯特采样频率对信号进行采样进而精确重构。传统的压缩感知为单测量向量(Single Measurement Vectors, SMV)模型,该模型仅在单点监测条件下利用稀疏性对信号进行采样获得测量数据,由此获得的测量信息比较单一,需要在不同点分别进行测量才能获得多个位置的信号数据。在单测量条件下对振动信号的监测和采样浪费大量时间,效率低,并且忽略了同一台机器不同监测点信号之间可能存在的相关性。因此对一台机器的多个测点同时进行监测,获得多测量数据信号,既可进一步利用数据间的相关性又在很大程度上减少信号的冗余性,更有利于对设备的运转状态进行判断,从而有效避免事故的发生。在多点监测条件下获得的测量向量不再是单测量向量而是多测量向量(Multiple Measurement Vectors, MMV),此时需要恢复的向量均为稀疏向量且具有公共支撑集,这种联合稀疏结构的重构问题称之为多测量压缩感知(CS-MMV)问题[3-5]。从多测量向量恢复未知的稀疏信号,被应用于压缩感知的联合稀疏重构,多测量向量的公共支撑集有利于获得更稳定、更精确的解。
稀疏恢复的本质问题是求解非凸优化问题。SMV模型的恢复算法主要有贪婪算法、凸松弛算法及其优化算法。Rao和Cotter证明,当无噪声存在时,利用MMV模型所求解的唯一性条件能从(N+1)/2增长至(N+L)/2。Duarte等[6-7]证明,若假定条件合适,则信号的准确重建率可随测量向量数L的增大呈指数倍增大。MMV模型信号的恢复可通过扩展SMV模型信号的恢复方法实现,如贪婪算法、凸松弛算法及其优化算法。但贪婪算法及其优化算法需要的测量数多,恢复精度低,不能保证所求解为全局最优解。凸松弛算法精度高,所需观测次数少,但计算复杂度高,易产生人工效应。稀疏贝叶斯算法[8-9]在解决信号内及信号间相关性比较强,时间结构相关性较强的信号时有很好的恢复效果。MMV问题的求解大多数应用于脑磁图学、传感器阵列信号处理[10]、稀疏通信信道的均衡、水下声波通道估计[11]、多任务压缩感知[12]等。 计算智能方法是求解组合优化问题的一种有效的现代智能方法。文献[13]将混合模拟退火算法应用于压缩感知的求解,提高了图像的重建精度。文献[14]基于遗传算法结合压缩感知将其应用于SAR高分辨距离像重构中,该方法可利用更少的测量数重构SAR场景目标。文献[15]将禁忌搜索算法应用于DOA估计中,该方法能获得全局最优解,并减少了计算量。粒子群算法是智能算法中求解复杂优化问题的一种高效方法,具有较强的全局寻优能力,在工程应用中具有深远意义。文献[16]将粒子群优化方法成功应用于SMV问题的稀疏恢复和图像重建中。文献[17-18]将粒子群优化方法成功地应用于MMV问题的稀疏恢复,重构精度得到很大提高。尽管针对MMV模型的稀疏恢复问题已有多种研究算法但鲜有研究针对机械振动信号。不同于上述研究,机械振动信号有其固有特性,采用多点监测振动信号的方法,大大缩短了采集不同位置振动信号所需的时间,提高了工作效率。多测量向量条件下,若仍采用传统的SMV重构方法将导致信号无法恢复。
针对上述问题,为精确重构多监测点条件下的机械振动信号,本文提出一种基于多测量向量模型的机械振动信号联合稀疏重构方法。尝试利用时间稀疏贝叶斯算法求得初始解,然后结合贪婪算法修剪技巧并加入自适应粒子激活机制进行位置更新,基于粒子群算法进行全局寻优,并通过选用西储大学轴承数据验证本文方法的有效性。
1 压缩感知基本理论
压缩感知理论[19]提出:若一个信号自身为稀疏信号,或者经某种变换基可表示为稀疏信号,则可通过一个与变换基不相干的测量矩阵将原始信号从高维空间投影至低维空间,得到一组远小于原始信号长度的观测值,再利用相关恢复算法由少许观测值恢复出原信号。
传统的压缩感知为SMV模型,其恢复可求解式(1)的l0范数问题
(1)
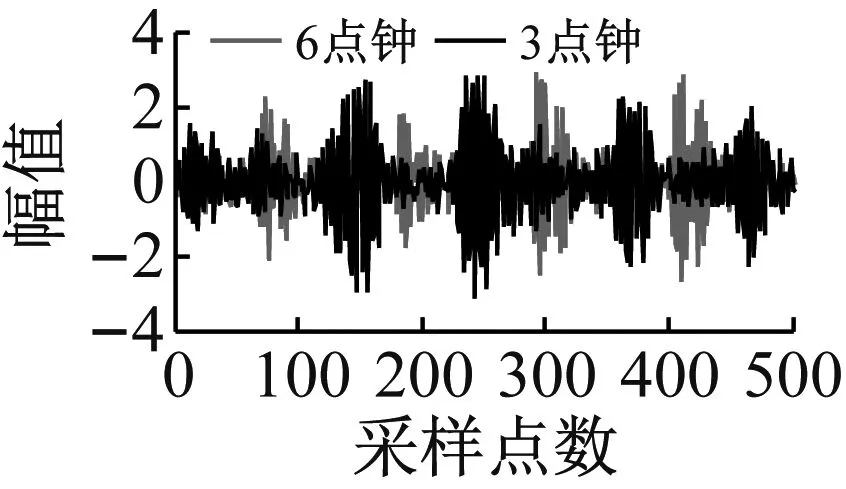
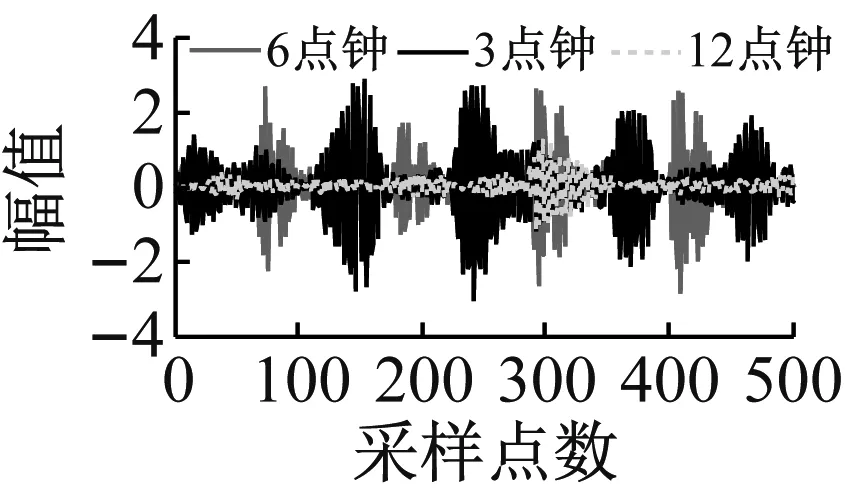
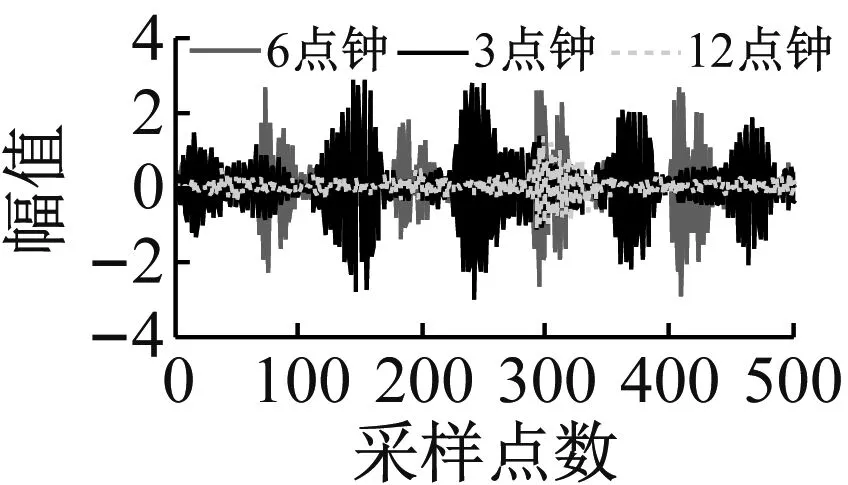
式中:f∈Rn为原始信号;Φ为m×n的测量矩阵;y为m维的观测值;θ为f经稀疏变换基Ψ表示的稀疏系数(θ中非零值的个数k< 联合稀疏恢复模型如下 (2) 式中:X∈RN×L为原始信号;B∈RM×L为观测值,θ为X在稀疏基ψ∈RN×N下的稀疏表示,Φ∈RM×N为观测矩阵,A∈RM×N为感知矩阵。式(2)的求解为NP难题,在测量矩阵满足约束等距条件时,联合重构问题最终转变为求解式(3)的l1范数最小化问题 (3) 式(3)可转变为下式 (4) 再通过式(5)重构原始信号 X=ψθ (5) 当测量值受到噪声污染时,其模型表示为 (6) 其中ΦX+N=B已知,N∈RM×L为高斯白噪声,δ≥0为已知噪声水平,显而易见,式(1)是噪声为零的特殊情况。 目前常用的联合稀疏重构算法有混合范数(M-BP)[20]、多重测量向量快速重构算法(MMMVFR)[21]、规则化(FOCUSS)算法[22]、正交匹配追踪法(M-OMP)[23]、时间稀疏贝叶斯算法(T-MSBL)、源自阵列信号处理的(MUSIC)算法[24]、一种性能可调的降维多测量向量与性能提升(ReMBo)算法[25]及以上算法的一些衍生算法等。 Kennedy等[26]从人工生命研究结果中受到启示,通过模拟鸟群搜寻食物和群聚的行为,提出一种模仿社会行为的启发式搜索算法:粒子群算法(Particle Swarm Optimization, PSO)。该方法不但具有概念清晰明了、容易实现、鲁棒性能强等特点,又有深刻的智能背景,在科学计算和工程应用有良好的表现,是一种非常有效的现代方法,该方法被广泛地应用于求解函数优化、神经网络训练、多目标优化、机器人、信号处理和组合优化等[27-28]各类复杂问题。 在粒子群算法中,设种群p={p1,p2,…,pN}由N个粒子组成,N为种群规模。粒子群中的每个粒子pi都表示一个可能的潜在解,通过所在位置xi和速度vi来描述,在d维空间内分别表示为xi={xi1,xi2,…,xid}和vi={vi1,vi2,…,vid},每个粒子在解空间中通过不断地“流动”飞行进行学习。pbesti表示粒子pi的当前最好位置(个体极值),gbesti表示所有粒子所飞行过的最好位置(全局最优位置)。PSO算法中,每个粒子通过式(7)更新自身速度和位置 (7) 式中:w为惯性权重,通常为非负常数;c1、c2为学习因子,一般情况下两者相等,取值范围为0~4;r1、r2为服从[0,1]分配的随机数。 标准的粒子群优化算法流程如表1所示。 基于粒子群算法,结合时间稀疏贝叶斯算法和贪婪算法的相关技巧,并加入一种自适应粒子激活机制,提出一种基于粒子群算法的机械振动信号联合重构算法(T-PSO)。粒子群算法的实现具体包括四个方面:群体初始化、适应度函数、更新机制、终止条件。 2.2.1 群体初始化 设种群规模为M,即共有M个粒子。PSO算法的全局寻优能力较强,而种群初始化对算法的性能有一定影响,初始种群与最优解越接近越有利于全局搜索,并可减少全局搜索时间。传统的粒子群算法采用随机化产生初始解,但如此产生的解通常质量较差。具有时间序列的稀疏贝叶斯算法(T-MBSL)不但在求解MMV模型时具有好的表现,当解决具有时序结构的MMV模型问题时算法恢复效果更佳。基于机械振动信号的固有特性,群体初始化采用T-MBSL算法,对全局搜索到最优解会更有利。其基本算法框架如表2所示。 表1 标准粒子群优化算法 表2 T-MSBL算法 2.2.2 适应度函数 (8) (9) 即: (10) (11) 此时问题(2)转换为求解式(12)的行支撑估计极小化问题 (12) 式中,ω由集合Ω中所有势均为K的子集组成的集合。 2.2.3 更新机制 粒子在PSO算法中的位置更新,通过自身经验和邻近经验进行。本文算法T-PSO基于种群进化策略和过程,并加入随机成分且结合贪婪追踪法中的修剪技巧,设计一种新的更新机制。由于粒子群算法在求解较为复杂的问题时易产生早熟,即当迭代未达到终止条件时,会出现粒子的个体最优位置和群体最优位置十分接近的情况,此时由于粒子的多样性降低、失去活性使得整个搜索进入局部搜索,从而会导致整个种群收敛于某个粒子的最优位置。在CS理论中,当测量值M增大时,粒子的搜寻范围和迭代次数也会增加,同时增加了粒子陷入早熟范围的概率。因此,为了降低这种情况出现的概率以及对重构精度的影响,T-PSO算法同时也加入了一种自适应的粒子激活机制。整体位置更新机制如下: (13) 定义第i个粒子迭代到第t次时的位置li,t为 (14) 此时考虑加入自适应粒子激活机制,一方面及时发现早熟、失去活性的粒子;另一方面及时改变失活粒子的搜索位置,从而避免其陷入局部搜索。 步骤1 首先判断粒子的个体最优位置是否过于接近全局最优位置,数学表达为两者的适应值之差很小,即: |F(li,pbest)-F(lgbest)|<η (15) 其中η=1×10-3。 若式(15)不成立,此时粒子未陷入局部搜索不进入激活机制,然后判断该粒子是否满足条件 F(li,t) (16) 若式(16)成立,则对个体粒子历史最优位置进行更新li,pbest=li,t,然后执行步骤2。 若式(15)成立,则进入激活机制,即: li,t=li,t+λ·randn() (17) 待失活粒子激活完成后,若满足式(15),然后更新个体粒子历史最优位置li,pbest=li,t然后执行步骤2。 步骤2 设第t次所有粒子位置全部更新完成后,种群的历史最优位置通过下式判断更新,若: F(lmin,t) (18) 2.2.4 终止条件 若F(lgbest)<ε或迭代次数达到预先指定的最大迭代次数tmax,则算法终止。 T-PSO算法流程如图1所示。 T-PSO算法流程如表3所示。 图1 T-PSO算法流程图 表3 T-PSO算法 步骤1 从美国西储大学轴承数据库,随机提取不同监测位置的两组机械振动信号数据X。 步骤2 分析该信号在DCT正交基Ψ下的联合稀疏性,获得联合稀疏度K,并对信号进行系数变换X=Ψθ,得到先验知识。 步骤3 选取随机高斯矩阵为测量矩阵Φ并对该信号进行压缩测量得到测量矩阵B(B=ΦX)。 步骤6 调整相关参数,重复步骤4~步骤5,比较不同参数下本文算法的有效性。 流程图如图2所示。 图2 机械振动信号重构算法流程 本文实验数据来自美国西储大学轴承数据库,该实验对象为深沟球轴承,将传感器分别安装在驱动端和风扇端进行故障数据采集,SKF6205是驱动端轴承,SKF6203是风扇端轴承。实验采用加速度传感器对振动信号进行采集,包含正常数据、轴承内、外圈故障数据、球故障数据,采样频率有4.8 kHz和1.2 kHz,故障直径的大小不同,分别为0.018、0.036/0.053 cm等,故障的状态负载分为0、1、2、3 HP(1 HP=746 W)。本实验选取轴承负载为0、采样频率为1.2 kHz的驱动端轴承外圈直径为0.018 cm的实验数据。 本文实验的所有数据均通过8 G运行内存、双核台式机的MATLABR2014a软件运行。实验结果均为50次独立实验的平均值。 为进一步验证多监测点条件下,本文所提算法(T-PSO)针对机械振动信号的联合稀疏恢复性能,本文实验均分为两组进行,第一组实验为监测点位置分别为3点钟和6点钟方向,两组长度均为512的两组轴承故障数据;第二组实验为监测点位置分别为3点钟、6点钟、12点钟方向,长度均为512的三组轴承故障数据。 机械振动信号大多是近似稀疏的,即在某种变换基下可为稀疏信号或者可压缩信号。常用的稀疏变换基有:散余弦变换基(DCT)、小波基(DWT)、傅里叶变换基(DFT)等,本文研究机械振动信号在DCT正交基下的联合稀疏性,同时估计其联合稀疏度K。 如图3所示为两组振动信号在DCT正交基下的变换系数,按绝对值由大至小降序排列后的系数分布图。如图4所示为三组振动信号在DCT正交基下的变换系数,按绝对值由大至小降序排列后的系数分布图。 图3 两组机械振动信号在DCT基下的变换系数衰减分布图 图4 三组机械振动信号在DCT基下的变换系数衰减分布图 多次实验后,信号均符合图3和图4的特征,由图可看出:两组实验的机械振动信号,在DCT正交基下的稀疏系数均呈现出明显的衰减趋势,且均在迭代150次时系数衰减曲线斜率急速降低且接近于零,所以两组实验的联合稀疏度K估计为150。该实验进一步验证了机械振动信号在DCT正交基下为可压缩信号。 本文实验用压缩率来衡量机械振动信号的可压缩性,其定义如下: 压缩率RC(Compression Rate, CR):表示振动信号的可压缩度。压缩率越大,则需要的测量数目越少,振动信号的可压缩力度越高。 (19) 式中:N为原机械振动信号长度;M表示经压缩后的信号长度。为了确保原始振动信号的高概率重建,压缩后的测量数M须满足如下不等式 (20) 式中,c≅0.28。 结合3.1节的分析,当N=512、K=150时,代入式(20)计算可得M≥52,联立式(19)和式(20)可得RC≤90%。由此可看出:对机械振动信号进行压缩采样时,压缩率最多不宜超过90%,否则当测量数目过少时,会出现原始振动信号不能被精确重构的现象。而当压缩率过小时,此时的测量数目过多,对于压缩采样而言没有任何意义。由分析可知压缩率不能过大或过小,因此本实验设置压缩率取值范围为60%≤RC≤90%,相应的采样值范围为52~200。 当无噪声存在时,本文采用式(21)定义的相对误差衡量机械振动信号的恢复性能。 当有噪声存在时,本文采用式(22)定义的均方误差衡量机械振动信号的恢复性能。 相对误差(Relative Error):绝对误差与原信号的比值。 (21) 压缩率过高或过低都会对压缩采样产生影响。压缩率过高时对采样时间和资源节约都比较有利,但不能保证信号被精确恢复;压缩率过低时则不利于传输和储存,失去压缩的意义。因此,选择合适的压缩率对信号的精确恢复很重要。 均方误差EMS(Mean Squared Error) (22) 其中均方误差越小,则信号恢复效果越好。 基于多测量向量模型,本文首先采用DCT正交基对信号进行稀疏表示,再通过随机高斯矩阵得到测量值,最后利用重构算法进行恢复。 MMV模型相比SMV模型能够减少恢复时间,提高重建准确率,由前述可知,MMV模型的重构算法可通过SMV模型的重构算法扩展而来,本文比较不同模型下正交匹配追踪算法的恢复性能。SMV、MMV模型下的正交匹配追踪算法分别记为OMP、M-OMP。 本实验设置测量值M=200,压缩率为60%时,验证正交匹配追踪算法针对两种模型的恢复效果。实验结果如表4和表5所示。 表4 SMV模型下OMP算法的重构性能 表5 MMV模型下M-OMP算法的重构性能 由表4可知,在SMV模型下要恢复3点钟和6点钟的信号所需时间为两者之和0.147 8 s;重构相对误差的平均值为0.516 5。而由表5可知在MMV模型下同时恢复3点钟和6点钟方向的信号即a组实验,仅需0.114 2 s;重构相对误差值为0.439 8。由表4可知,在SMV模型下要恢复3点钟、6点钟和12点钟的信号所需时间为三者之和0.209 7 s;重构相对误差的平均值为0.555 0。而由表5可知在MMV模型下同时恢复3点钟、6点钟和12点钟方向的信号即b组实验,仅需0.143 2 s;重构相对误差值为0.425 0。由此可看出相比SMV模型而言,MMV模型可减少重构时间,降低重构误差,提高重建精确率。 由于压缩率过高或者过低会对原信号的压缩采样、存储和传输、重构精度产生影响,本实验选取压缩率固定为65%,测量数目M=180时,验证不同算法针对机械振动信号的重构相对误差和恢复波形图,实验结果如表6和图5所示。 表6 固定压缩率下不同算法的重构性能比较 由表6可知:当压缩率固定为65%时,不论是a组实验还是b组实验,M-OMP算法的重构相对误差都最大,M-FOCUSS、M-SBL和T-MSBL三种算法的重构相对误差在逐渐减小,但本文所提算法T-PSO的重构误差最小,只有M-OMP算法的50%。 由图5直观看出:当固定压缩率为65%时,两组实验相比其它算法,采用本文所提算法T-PSO所恢复的机械振动信号与原振动信号差异最小,几乎完美重构,这与表6不同算法恢复振动信号的重构相对误差结果一致。因此,结合图5和表6可知:本文所提算法T-PSO针对多监测点条件下的机械振动信号的恢复效果最好,重构相对误差最小,具有更好的适应性。 本实验设置测量值变化范围为60≤M≤270,验证T-PSO算法随测量值变化的重构性能。实验结果如图6所示。 (a) 原始信号 (b) M-OMP (c) M-FOCUSS (d) M-SBL (e) T-MSBL (f) T-PSO (a) 原始信号 (b) M-OMP (c) M-FOCUSS (d) M-SBL (e) T-MSBL 由图6可知:随着测量值的增加,即压缩率减小时,两组实验中不同算法的重构相对误差均在减小。其中,M-OMP的重构相对误差最大;M-FOCUSS算法、M-SBL算法、T-MSBL算法的重构相对误差次之;本文所提算法T-PSO算法的重构相对误差最小,针对机械振动信号的重构效果最好。并在测量值大于200时,不同算法的曲线变化趋势均不再明显,接近最小值,这与前述分析测量值的变化范围一致:当测量值数目过大,压缩没有任何意义,测量值数目过小,原机械振动信号无法精确重构。 当信噪比较高时,采集到的信号所包含的有用信息较多;而信噪比较低时,所包含的有用信息则较少。 (a) 两组机械振动信号恢复效果 (b) 三组机械振动信号效果恢复图 因此,当有噪声存在时,信噪比的高低会对信号的恢复性能有一定影响,本实验假设噪声为高斯白噪声,设置信噪比取值范围5~35 dB时,验证噪声存在时T-PSO算法针对机械振动信号的恢复性能。实验结果如图7所示。 图7表明:当有噪声存在时,随着信噪比的增大,两组实验中不同算法的重构均方误差均在减小。其中M-OMP算法的重构均方误差最大;M-FOCUSS算法、M-SBL算法、T-MSBL算法的均方误差次之;本文T-PSO算法的重构均方误差最小,即恢复最为精确。并且RSN>20 dB时,重构均方误差变化不再明显,几乎达到最小值。如图8所示为噪声存在时a组实验的机械振动信号波信号图和b组实验的机械振动信号波信号图。 由图8可知:随着信噪比的增大,两组机械振动信号的波形图与原始振动信号波形图均逐渐接近。当信噪比为5 dB时,此时的波形图与原振动信号波形图相差最大,这是由于信噪比较低时,信号中所包含的有用信息较少;当RSN=10 dB、RSN=15 dB时,波形图逐渐与原振动信号波形图相近;当RSN=20 dB时,此时波形图与原振动信号波形图几乎一致;当信噪比为RSN=25 dB时,同样几乎重现原振动信号,这是由于信噪比较高时,信号中所含有的有用信息较多,即包含原信号的信息较多,此时更有利于对含有噪声的信号进行重构恢复,这与图8所示的机械振动信号随噪声变化的曲线图结果一致。 (a) 两组机械振动信号恢复效果 (b) 三组机械振动信号恢复效果 针对传统压缩感知的测量模型为单测量向量模型,此时获得的数据单一,采样浪费时间、效率低等问题,本文提出了一种基于多测量向量模型的机械振动信号联合稀疏重构算法。选用DCT基进行稀疏性分析,随机高斯矩阵为测量矩阵,最后利用粒子群算法结合时间稀疏贝叶斯算法搜索全局得到最优解。各项实验表明: (1) 在多监测点条件下,随着测量数的增加,即压缩率的减小,每种算法的恢复重构误差都越来越小,但本文所提方法总具有最优性能。 (2) 当有噪声存在时,本文所提方法也具有最小的重构均方误差。在机械振动信号的应用上具有一定的理论意义与应用价值。 (a) 原始信号 (b) RSN=5 dB (c) RSN=10 dB (d) RSN=15 dB (e) RSN=20 dB (f) RSN=25 dB (a) 原始信号 (b) RSN=5 dB (c) RSN=10 dB (d) RSN=15 dB (e) RSN=20 dB (f) RSN=25 dB
2 基于多测量向量模型的机械振动信号重构方法研究
2.1 粒子群优化算法
2.2 基于粒子群算法的联合稀疏恢复算法设计






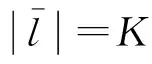
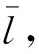

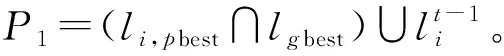
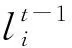



2.3 基于多重测量模型的机械振动信号重构算法实现步骤


3 实验与分析
3.1 机械振动信号联合稀疏度分析


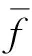
3.2 SMV模型与MMV模型恢复性能分析


3.3 固定压缩率下,T-PSO算法的性能分析

3.4 测量值变化时T-PSO算法的性能分析










3.5 噪声存在时T-PSO算法的性能分析




4 结 论