参外联合激励下一类混沌系统的动力学机理
2021-01-18张晓芳董颖涛韩修静毕勤胜
张晓芳, 董颖涛, 韩修静, 毕勤胜
(江苏大学 土木工程与力学学院, 江苏 镇江 212013)
自1963 年三维 Lorenz系统中的混沌现象被揭示以来[1-3],混沌及其机理的研究一直是学术界的广泛关注的课题之一[4-6]。各类不同的混沌系统,如Rossler振子[7-8]、Chen系统[9-12]、蔡氏电路[13-15]等纷纷被建立起来。基于双翼混沌吸引子的Lorenz混沌系统,Sara Dadras等通过改变该系统的非线性结构,其相应的数学模型[16]为

(1)
得到了一类由倍周期分岔导致的新型四翼混沌吸引子[17-18],该数学模型可通过EWB软件设计的电子振荡电路实现。同时,在该电路的基础上通过引入两频率不同的周期电流源,使混沌系统进入周期运动状态,以达到控制系统运动的目的[19-20]。
迄今为止,相关工作大都是围绕常规激励频率开展的,并着重考察了不同共振形式下的解特性,而当激励频率与系统固有频率之间存在量级差距时,会产生不同尺度的耦合效应[21-22],导致一种特殊的振荡行为,也即系统的状态变量会在大幅振荡和微幅振荡之间来回转换的簇发振荡。簇发振荡在许多工程及科学问题中都有所涉及,其中生物神经元在外部刺激作用下信息的传递和交换是一种典型的簇发振荡形式[23-25]。
为揭示这种特殊振荡的产生机制,Rinzel提出了快慢分析法,也即将系统视为快慢子系统的耦合,通过分析快子系统的分岔及慢子系统的调节行为,得到各种簇发振荡机理[26-29]。该方法对于自治快慢耦合系统非常有效,基于该方法,Izhikivich[30]总结了一快一慢和两快一慢耦合系统中几乎所有簇发振荡的模式,并提出了按照沉寂态和激发态转换时的分岔将簇发振荡分类的方法。
而对于周期激励系统,当激励频率远小于系统的固有频率时,由于没有明显的快慢子系统,不能直接应用Rinzel的快慢分析法。为此,本课题组拓展了该方法,也即将整个周期激励项视为慢变参数,并相应组成慢子系统,而原系统则转换为广义自治系统,构成快子系统[31-32]。基于这一思想,得到了单周期外激和参激下各种振子中不同的新型簇发振荡模式及其机理。
在相关工作的基础上,本文将进一步考察两种周期激励,也即参外联合激励下系统的两尺度耦合效应,以Sara Dadras的四翼混沌吸引子为例,重点探讨当激励频率远小于系统固有频率时,两激励频率形成不同共振关系及共振关系受扰动情形下系统的动力行为,揭示各种不同簇发振荡的产生机制及其相互演化的规律。
1 严格共振下的分岔分析
在系统(1)的基础上,同时引入周期激励和参数激励,得到了三维非自治系统
(2)
式中,wi=Aicos(ωit)(i=1,2)分别为系统的参数激励和周期外激励,Ai(i=1,2)为激励幅值,ωi(i=1,2)为相应的激励频率。ωi(i=1,2)的不同比值可以实现不同的共振形式。当系统(2)中的2个激励频率ωi(i=1,2)均远小于系统的固有频率ΩN时,系统存在多个时间尺度。
由于ωi/ΩN<<1(i=1,2),令t∈[t0,t0+TN],其中TN=2π/ΩN,在任意一个以t=t0作为初始时间点的固有周期TN内,周期激励项WAi=Aicosωit0(i=1,2)和WBi=Aicos(ωit0+2πωi/ΩN)(i=1,2)之间变化,期间Aicosωit(i=1,2)几乎保持不变。因此,可以将Aicosωit(i=1,2)视为系统(2)的2个慢变参数,相应地,系统(2)可称为关于2个慢变量的广义自治系统。当2个频率满足严格的整数比关系时,可以采用Moivre公式[33],将w=cos(ωit/n)(n为正整数)定义为基本慢变量,利用函数fi(w)(i=1,2)来分别表示这2个慢变量,即w1=A1f1(w),w2=A2f2(w)。则系统转化为只含有1个基本慢变量w的快慢系统。这样,可以应用传统的快慢分析法来揭示参外联合激励下系统不同簇发行为产生的机理。
不妨将广义自治系统的平衡点定义为E(xi0,yi0,zi0),其中
不难得到,xi0满足

(3)
平衡点的稳定性由其对应的特征方程决定,即
λ3+a2λ2+a1λ+a0=0
(4)
其中特征方程的系数分别为

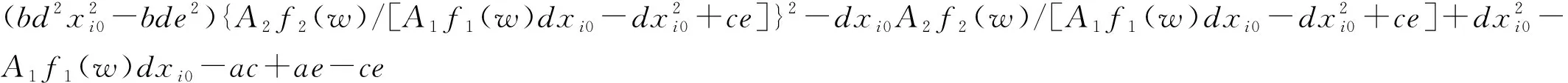
a2=a-c+e
(5)
根据Routh-Hurwitz准则可知,当式(4)满足条件a0>0,a2>0,a1a2-a0>0时,平衡点E(xi0,yi0,zi0)是稳定的。而平衡点的失稳会导致不同形式的分岔。当特征方程有零特征根时,系统可能出现Fold分岔,用LB表示Fold分岔集,即
LB:a0=0
(6)
当特征方程的特征值含有一对纯虚根时,系统可能产生Hopf分岔,用HB表示Hopf分岔集,即
HB:ai>0(i=1,2,3)且a0=a1a2
(7)
此时,由Hopf分岔产生的频率为
(8)
为了进一步讨论共振条件下系统的动力学行为,文中取定参数a=2,b=7,c=2,d=6,e=9,A1=2,A2=10。利用Moivre公式将两个慢变量转化为一个基本慢变量w表示,其中w=cos 0.01t。表1给出了ω1∶ω2=2∶4,1∶3三种典型的不同频率比下f1(w)和f2(w)的表达式。
图1给出了三种不同频率比下的平衡曲线图及其分岔图。其中实线表示稳定的平衡点,虚线表示不稳定的平衡点,HB表示Hopf分岔点,FB表示Fold分岔点。由图1(a)可知当ω1∶ω2=1∶1时,系统有3条平衡线,其中包括4段稳定的平衡线,3段不稳定的平衡线,稳定的平衡线与不稳定的平衡线之间由4个超临界Hopf分岔点连接,2个Fold分岔点位于中间的不稳定平衡线上,平衡线关于原点呈中心对称。

表1 不同激励频率比下f1(w)和f2(w)表达式
由图1(b)可知,当ω1∶ω2=2∶4时,系统包含10段稳定的平衡线和9段不稳定的平衡线,平衡线关于w=0呈轴对称。由图1(c)可知,当ω1∶ω2=1∶3时,系统包含8段稳定的平衡曲线和7段不稳定的平衡线,平衡线关于原点呈中心对称。比较不同频率比下的平衡线曲线可以看出,虽然系统中激励的频率比在变化,但3条平衡线数目不发生变化。不同的是其平衡线的结构发生了变化,平衡线在x=0处来回穿插,相对于图1(a),图1(b)和1(c)中一个周期内平衡点正负改变的次数增加,使得分岔点数量也相应增加,系统的动力学特性更加丰富。

(a) ω1∶ω2=1∶1平衡线图

(b) ω1∶ω2=2∶4平衡线图

(c) ω1∶ω2=1∶3平衡线图

(d) ω1∶ω2=2∶4平衡线局部放大图
2 严格共振条件下的簇发振荡
2.1 情形一



(a) 时间历程图

(b) (x,y)平面相图

(c) 平衡线图与(w,x)平面转换相图的叠加图

(d) x方向上系统速度时间图
从图2(c)中可以观察到,系统轨线在经过Fold分岔点向上跳跃时发生了轨线局部突出的现象。结合变量x的速度时间图2(d)可知,轨线在B点处速度瞬间增大,又在短时间内迅速回落至负方向导致了在此处x值的迅速变化。
2.2 情形二



(a) 时间历程图

(b) (x,y)平面相图

(c) 平衡线图与(w,x)平面转换相图的叠加图

(d) 叠加图局部放大图1

(e) 叠加图局部放大图2
2.3 情形三
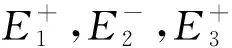

(a) 时间历程图

(b) (x,y)平面相图
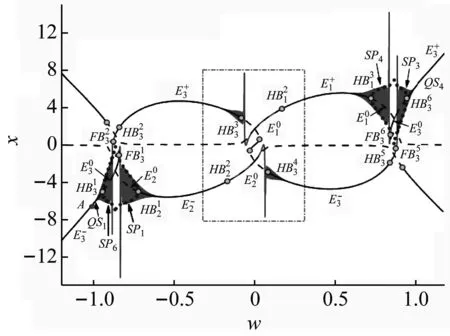
(c) 平衡线图与(w,x)平面转换相图的叠加图

(d) 叠加图局部放大图

从上述三种情形可以看到,当外激励频率远小于系统固有频率时,系统产生了簇发振荡。在参外联合激励处于共振的条件下,随着激励频率比的变化,广义自治系统的平衡线发生了改变,导致参外联合激励系统不同的簇发现象,在系统相图上则表现为涡卷数目的变化,即由双涡卷现象逐渐演化为动力学特性更为丰富的四涡卷现象。
3 非严格共振条件下的簇发振荡
3.1 簇发振荡
严格的共振情况在实际系统中很少存在,系统往往受到不同程度的扰动。在小扰动的情况下,系统的动力学行为将会更为复杂.
在上述严格共振情况下,采用Moivre公式将两个慢变量转化为一个基本慢变量的分析方法,在此不再适用。为了解决这一问题,本文将慢变频率之一与时间的乘积作为慢变参数。在确定了慢变参数和对应的广义自治系统后,即可分析不同频率比下系统的平衡点的演化,以及相应系统的簇发振荡,从而揭示其产生的机理。
取定各参数与共振情况相同,保持频率ω1=0.01不变,ω2在0.01附近产生一定的扰动,取ω2=0.011。以τ=0.01t作为慢变量,图5(a)为系统随慢变量τ变化下的平衡线图。由平衡线图可以看出,系统的平衡点分支由三条平衡线组成并呈现周期状态,其周期为2 000π。图5(b)为(τ,x)平面上的转换相图与平衡线叠加图。假定系统轨线在τ=100时,位于下半平面的小领域内,则在此后轨线会沿着稳定的平衡点分支运动,此时系统处于沉寂态,当遇到Fold分岔点时,系统向上跳跃,同时受到Hopf分岔点的影响,平衡点失稳发生大幅振荡,进入激发态,随着τ增加,振荡幅度减小,在稳定平衡线处,轨线退出激发态,再次归于沉寂态。轨线之后的运动与此类似,不再赘述。与频率比为ω1∶ω2=1∶1的情况相比,虽然外激励频率发生了微小扰动,但非共振情况下,系统的动力学行为发生了巨大变化。不仅系统的周期增加,系统的平衡线结构也发生了很大变化。在小扰动的情况下,一个周期内,平衡线的波峰与波谷的数量急剧增加,使得轨线周期运动中激发态和沉寂态转换的次数增加,在相图上表现为涡卷的叠加如图5(c)所示,使得系统的动力学特性变得更加复杂。
3.2 不同频率比的影响
当参外联合激励的频率比为ω1∶ω2时,设
(9)
p与q为互质的正整数,则系统的最小周期在真实时间上为
(10)
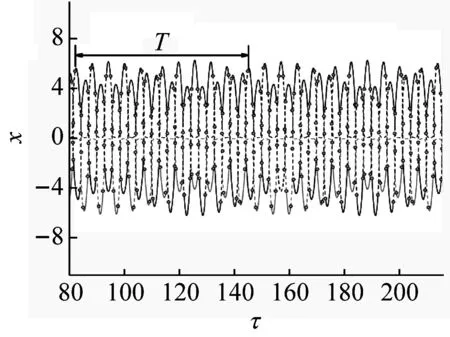
(a) 平衡线图

(b) 平衡线图与(τ,x)平面转换相图的叠加图

(c) (x,y)平面相图
如上述例子中ω1=0.01,ω2=0.011时,周期为T=2π/0.001=2 000π。可见,当系统的频率受到一定程度的扰动时,系统的周期大大延长了,同时簇发的稳定性也会一定程度的影响。值得注意的是,当γ取无理数时,系统进入非周期运动,即使当γ取有理数时,系统也并不一定是周期运动,也可能是概周期运动,甚至可能是混沌现象。
将参数激励的频率固定为0.01,在0.009~0.015之间改变外激励的频率,探讨系统在不同频率比时的动力学演化行为。
从庞加莱截面图6~10可以看出,当ω1∶ω2=1∶1和ω1∶ω2=1∶1.5时为周期运动,当ω1∶ω2=1∶0.9和ω1∶ω2=1∶1.1时均为概周期运动。从系统Lyapunov指数与参数ω2的关系图中,也可以看到,随着频率比的改变,Lyapunov指数并没有出现大于零的情况,可以推断,系统并未进入混沌状态,所以系统随着频率比的改变,呈现出周期运动与概周期运动交替变化。

(a) 三维相图

(b) 庞加莱截面
4 结 论
参外联合激励下的混沌系统在激励频率远小于系统固有频率时会存在明显的两时间尺度效应。当两激励频率处在严格共振情形时,利用Moivre公式可以将两个激励项转化为均含一个基本激励项的代数表达,从而可以将该基本激励项视为慢变参数,得到相应的广义自治系统,基于该广义自治系统随慢变参数的平衡点曲线及其分岔分析,结合转换相图,揭示相应簇发振荡的分岔机制。可以发现,参外联合激励从到共振,由于平衡曲线分布方式及相应分岔点数量的不同,导致了快慢耦合系统的轨线在不同的平衡点之间跳跃的次数增加,由围绕着两个焦点的簇发振荡,转变为围绕三个焦点乃至四个焦点的簇发振荡,在相图上表现为涡卷数量的变化,从两涡卷,三涡卷到四涡卷。而当两激励频率处在非严格共振情形时,由于无法采用Moivre公式简化,为此,可以将慢变频率之一与时间的乘积作为慢变参数,从而得到该情形下相应的广义自治系统。同样,基于随慢变参数变化的平衡曲线及其分岔分析,结合转换相图,揭示簇发振荡的产生机制。我们发现,与严格共振情形不同,非严格共振时,平衡曲线的周期大大延长了。同时,一个周期中平衡曲线上存在的分岔的数目也显著增加了,这就导致耦合系统的轨线经过分岔点时激发态和沉寂态转换次数也随之增加,使得系统的动力学行为更加复杂。另外,从庞加莱截面图以及Lyapunov指数计算可以判断,随着频率的变化,系统呈现出周期与概周期簇发振荡交替变化的运动特征。
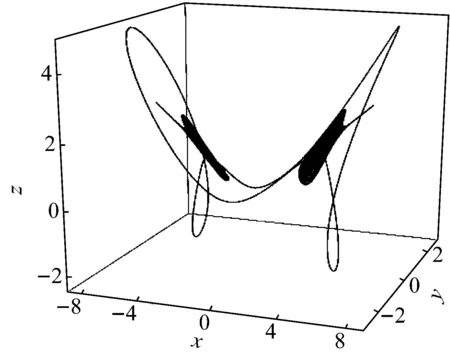
(a) 三维相图

(b) 庞加莱截面

(a) 三维相图

(b) 庞加莱截面

(a) 三维相图

(b) 庞加莱截面

图10 Lyapunov指数与参数ω2的关系
