不同冲击幅值下洞室围岩变形-开裂-垮塌过程<br/>——基于连续-非连续方法

不同冲击幅值下洞室围岩变形-开裂-垮塌过程
——基于连续-非连续方法

2021-01-18王学滨钱帅帅

振动与冲击 2021年1期

王学滨，田锋，钱帅帅

(1.辽宁工程技术大学计算力学研究所，辽宁阜新 123000；2.辽宁工程技术大学力学与工程学院，辽宁阜新 123000)

在防护和采矿等工程中，洞室围岩常会受到不同形式的冲击载荷作用。冲击载荷来源于爆破、断层错动、煤柱失稳和岩层断裂等。在深部高地应力下，冲击载荷往往会诱发岩爆、冒顶、片帮、垮塌和冲击地压等灾害，造成重大人员伤亡和设备损坏。例如，在采矿工程中，断层失稳错动可诱发强烈的冲击载荷，从而导致重大断层冲击地压事故。2011年河南义马千秋煤矿发生一起重大断层冲击地压事故，造成10人死亡，60多人受伤，近400 m巷道顶板垮塌。采矿工程中的岩层周期破断、断层周期黏滑和反复爆破是较为常见的。因此，探索周期冲击下洞室围岩的变形-开裂-垮塌过程具有重要理论和实际意义。

在实验室中，探索洞室围岩的变形、破坏和稳定性规律的重要思路之一是将先或后开挖孔洞的(类)岩石作为洞室围岩本身开展相关研究[1-2]。常见的此类实验主要包括单轴压缩实验、双轴压缩实验、三轴卸载实验[2]、动力加载实验[3-4]和动静载组合实验[5]等。近年来，已取得了显著的进展。有些实验很好地再现了现场的若干观测结果，从而对洞室围岩有关破坏规律的认识有了根本性的提升。例如，剥落一方面促进了屈曲大变形，另一方面弱化了岩体的强度，从而诱发了岩爆；剥落与岩爆强烈相关[6]；随着冲击载荷幅值和频率的增加，应变型岩爆更易发生[7-8]，等等。

在数值模拟研究方面，关于冲击或周期冲击下洞室围岩的变形、破坏和稳定性规律的认识也在不断深化。例如，李夕兵等[9]将冲击载荷简化为幅值为30～90 MPa的1个简谐波，采用PFC2D研究了冲击载荷幅值对巷道围岩的应力场、位移场及破坏区范围的影响；陈建军等[10]将周期冲击载荷简化为幅值为10 MPa的周期半正弦应力波，采用FLAC3D研究了周期冲击载荷作用位置和方向对矩形巷道两帮、顶、底板速度和加速度的影响。应当指出，上述文献多采用连续方法(例如，FLAC3D[10])和非连续方法(例如，PFC[9])开展研究，主要呈现了洞室围岩的塑性区、应力、应变和位移等力学量的时空分布规律，一般不涉及洞室围岩的局部开裂规律。大量实践证明，在实验室和现场观测中，洞室围岩的开裂更多的是局部开裂(例如，出现1～4个V形坑[11-13])。

采用连续方法可以较好地模拟洞室围岩的应力、应变及塑性区分布，但不适于模拟洞室围岩的开裂和坍塌过程；采用非连续方法可以较好地模拟节理围岩的岩块运动和岩块之间的相互作用，但往往需要引入接触刚度，这会对应力、应变产生一定影响。为了弥补连续方法和非连续方法的各自缺陷，连续-非连续方法应运而生，发展迅速[14-17]。本文第一作者团队经过多年努力发展了拉格朗日元与变形体离散元耦合的连续-非连续方法，适于模拟连续介质向非连续介质转化和非连续介质进一步演化，已对其正确性在各方面进行了检验，并取得了一些良好的研究进展。例如，王学滨等[17]模拟了位移控制加载下三点弯梁的变形-开裂过程，探讨了尺寸效应的影响。

本文在自主开发的拉格朗日元与变形体离散元耦合的连续-非连续方法中同时引入Ⅰ型和Ⅱ型断裂能。模拟了周期半正弦波冲击下洞室围岩的变形-开裂-垮塌过程，阐明了应力波反射和叠加导致洞室顶板开裂机理，解释了洞室两帮拉、剪裂相伴现象的原因，探讨了周期冲击载荷幅值的影响规律。

1 连续-非连续方法简介

拉格朗日元与变形体离散元耦合的二维连续-非连续方法[18]主要包括应力、应变模块、节点分离模块、接触力求解模块和运动方程求解模块。应力、应变模块通过节点的速度利用高斯定理求解单元的应力和应变。接触力求解模块首先通过基于空间剖分的单元接触检测方法进行接触检测；然后，通过基于势的接触力计算方法求解发生接触的单元的接触力；最后，通过法向接触力、切向接触力和摩擦系数求解有关节点的摩擦力。运动求解模块通过节点力利用牛顿第二定律求解节点的速度。

下面对节点分离模块进行介绍。

(1) 节点分离判断。分别选择最大拉应力准则(σ3>σn，σ3为最大主应力，σn为抗拉强度)和莫尔-库仑准则作为节点拉伸、剪切分离判据。节点的应力由节点周围单元的应力取平均获得。

(2) 分离方向选择。当节点的应力满足上述强度准则时，需计算理论开裂方向(拉裂的理论开裂方向与σ3方向垂直；剪裂的理论开裂方向与σ3方向的夹角为45°+φ/2(φ为内摩擦角))，选取与理论开裂方向最接近的单元边界作为实际开裂方向。应当指出，可以通过加密网格来避免上述开裂方式带来的网格依赖性问题。以图1(a)为例，①～④代表单元，若节点A满足剪切分离条件，假定理论分离方向为图1(a)中虚线，需从潜在分离方向1～3中选择与理论分离方向夹角最小的单元边界(图1(a)中AB边)作为实际分离方向。应当指出，在节点发生分离之后，若需要进行大量的接触检测，则计算效率有待进一步提高。

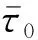
(a)

(b)

(a)

(b)

当虚拟裂缝刚出现时(图3)，σn和τs达到最大；随着w和s的增加，σn和τs线性下降；当w和s分别达到自身的临界值wp和sp时，σn和τs分别降为0。σn和τs的计算公式具体如下

(1)

图3 两个单元之间的黏聚力

在本文第一作者团队发展的连续-非连续方法的早期版本中[17]，只引入了Gf,Ⅰ，而未引入Gf,Ⅱ。当时的主要考虑一方面是Gf,Ⅱ不易测量，另一方面τs计算原理更简单。在早期版本的方法中，当节点无论刚发生拉伸分离和剪切分离时，均需用面内剪应力替代τs的最大值。当σn消失时，τs也消失，以此简化处理避免Gf,Ⅱ的引入。上述简化处理对于拉裂模拟较为有效，针对直接拉伸、三点弯曲[17]等条件下的模拟结果与有关的理论结果或实验结果吻合较好。然而，上述早期版本的方法不适于模拟剪裂峰后软化现象，只能模拟出剪裂峰后脆性现象，适用性有限。现引入Gf,Ⅱ之后，可以更好地模拟拉、剪裂缝的扩展过程。

当前的考虑是无论节点发生何种形式分离，均引入Gf,Ⅰ和Gf,Ⅱ。当节点发生拉伸分离时，引入Gf,Ⅱ的目的是为了弥补虚拟裂缝面上节点切向弹性力的突然消失(在节点分离之前，通常，节点的弹性力并非在水平或垂直方向上，而是在两个方向上都有分量)；当节点发生剪切分离时，引入Gf,Ⅰ的目的是为了弥补虚拟裂缝面上法向弹性力的突然消失。所以，上述考虑内容能有效避免计算模型发生剧烈震荡，有助于提高该方法的准确性。

2 计算模型及方案

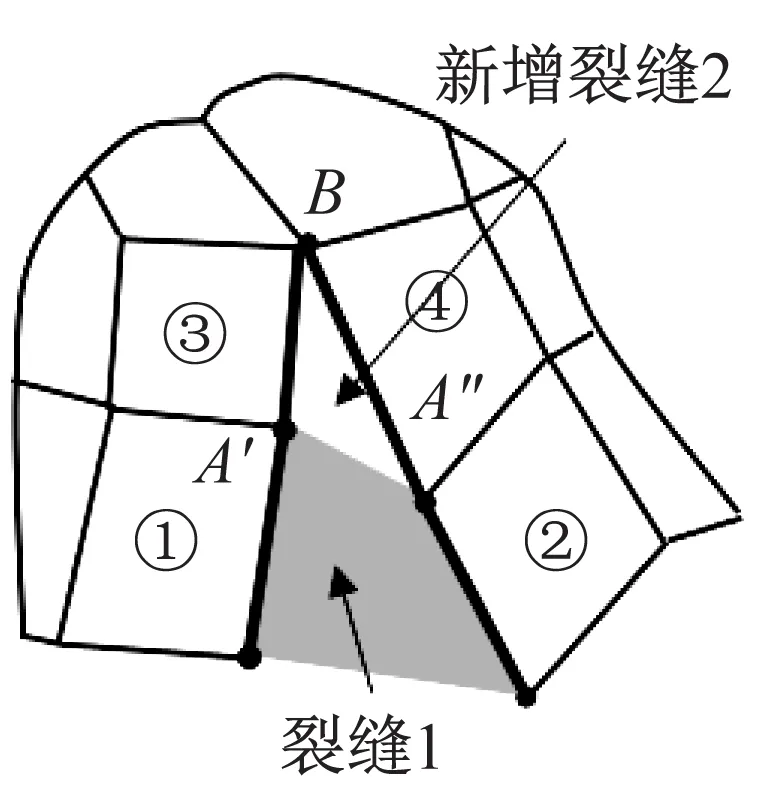
本文的洞室围岩模型(以下简称模型)的建立依据济三煤矿123下04工作面的某一巷道围岩。该煤矿位于山东省西南部济宁市南郊，深受冲击地压危害。据不完全统计，该煤矿自2003年以来累计发生冲击地压8次。将未开挖前的模型视为连续介质，模型不涉及大型结构面。模型的高度和宽度均为40 m，被剖分成160×160个正方形单元，单元尺寸与模型高度之比为1/160，相比之下，单元尺寸足够小，网格依赖性应较小。在模型下端面，施加竖向铰支座约束，在左、右侧面和上端面，施加27 MPa的压应力(图4)。参数取值如下：面密度ρ=2 700 kg/m2，弹性模量E=20 GPa，泊松比μ=0.3，抗拉强度σt=5 MPa，法向刚度系数Kn=10 GPa，莫尔-库仑准则中的黏聚力c=20 MPa、φ=40°，摩擦因数f=0.1，Gf,Ⅰ=100 N/m，Gf,Ⅱ=4 000 N/m，局部自适应阻尼系数α=0.2，该值在动力模拟中常被采用，时步长度Δt=1.979 24×10-5s，Δt小于临界时步长度(7.919 6×10-5s)，以确保数值稳定性。计算在平面应变、大变形下进行。应当指出，模型的左、右侧面和上端面均为透射边界。

图4 开挖后的模型

计算过程可分为：

步骤1 对开挖前的模型进行计算，直到模型达到静力平衡，该步骤所用时步数目N为12 000；

步骤2 从开挖前的模型中心处逐圈删除单元，以开挖6 m×6 m的正方形洞室(所用N为4 000)，洞室中心与开挖前的模型中心重合，直到开挖后的模型达到静力平衡，该步骤所用N为8 000；

步骤3 在模型的上端面，施加竖直向下的冲击载荷P(t)，该步骤从N=20 000时开始，所用N为4 000。本文将P(t)简化为半正弦压应力波(共有8个压应力波传入模型)，P(t)-时间t曲线见图5。P(t)表达式如下

P(t)=

(2)

式中:Pmax为压应力波幅值;圆频率ω=318.395 rad/s;t=NΔt;0.395 848 s和0.475 017 6 s分别相当于N=20 000时和N=24 000时；

步骤4 对冲击下模型进行计算。

图5 冲击载荷-t曲线

共采用4个计算方案。方案1～方案4的Pmax分别为16 MPa、13 MPa、10 MPa及7 MPa。在现有技术条件下，Pmax在现场难以实测。本文的Pmax的取值涵盖了现有文献[19]的合理取值范围。

3 计算结果及分析

3.1 图片说明

图6为方案1的拉裂缝与最大主应力σ3的时空分布规律，图7为方案1的剪裂缝与最小主应力σ1的时空分布规律，图8为方案3的拉裂缝与σ3的时空分布规律，图9为方案3的剪裂缝与σ1的时空分布规律。其中，在图6和图8中黑色线段代表拉裂缝区段；在图7和图9中，黑色线段代表剪裂缝区段。应当指出，两个单元之间的裂缝称之为1个裂缝区段，裂缝区段的形状为四边形。若干裂缝区段连在一起构成裂缝。考虑到单元脱离围岩后裂缝将变得很大，图6～图9仅显示了各边长度均小于等于1个单元边长的裂缝区段。图10和图11分别给出了方案1～方案4的拉裂缝区段数目Nt和剪裂缝区段数目Ns随N的演变规律，统计的Ns和Nt包括图6～图9中显示的和未显示的裂缝区段。

3.2 冲击下洞室围岩的变形-开裂-垮塌过程

3.2.1 多个压应力波冲击下拉、剪裂缝的时空分布

下面，以方案1为例进行分析。

由图6和图7可以发现，拉裂缝首先产生在洞室顶板，然后产生在洞室两帮；拉裂缝主要分布在洞室顶板；剪裂缝主要分布在洞室两帮，形成V形坑。拉、剪裂缝发展过程具体如下：

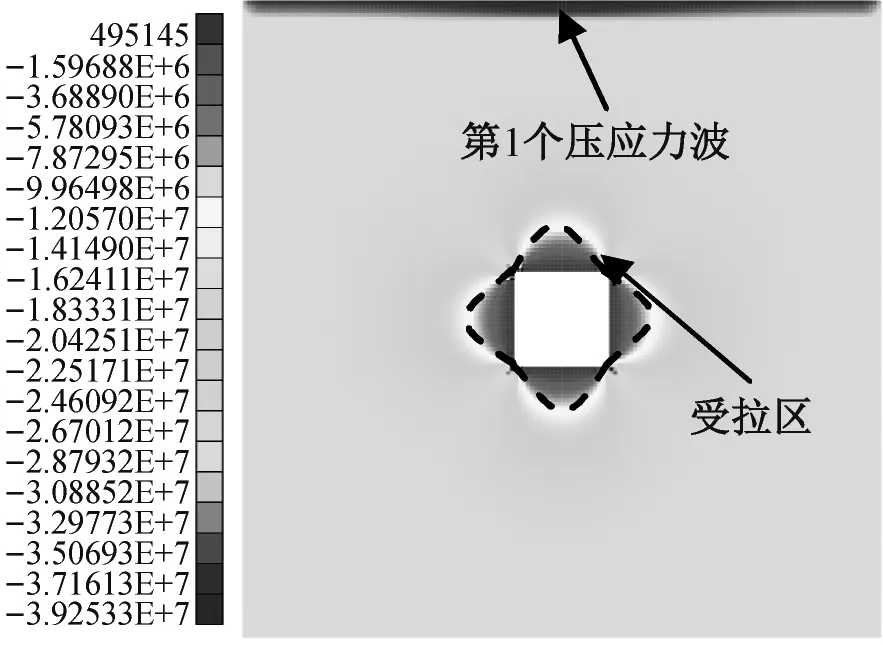
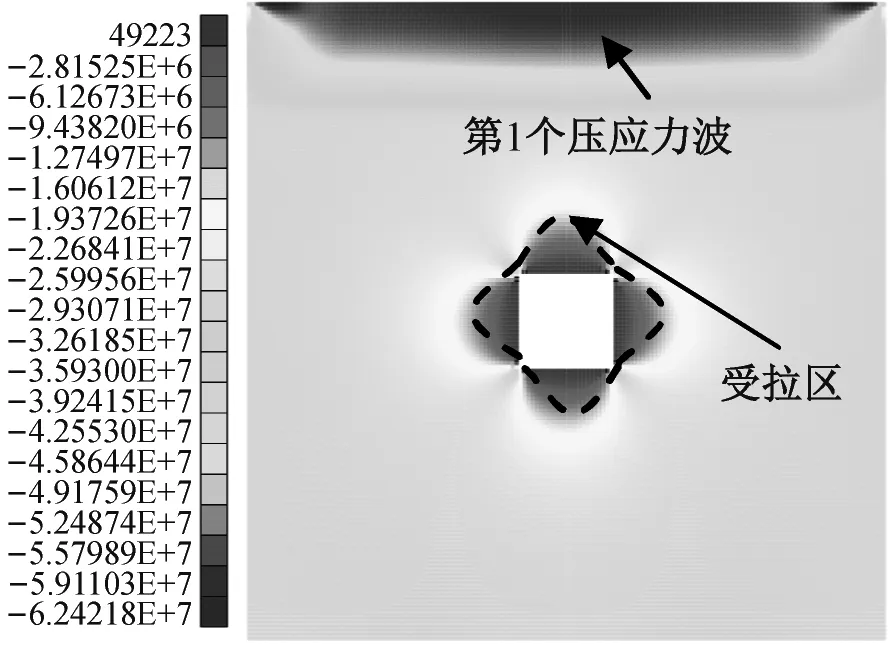
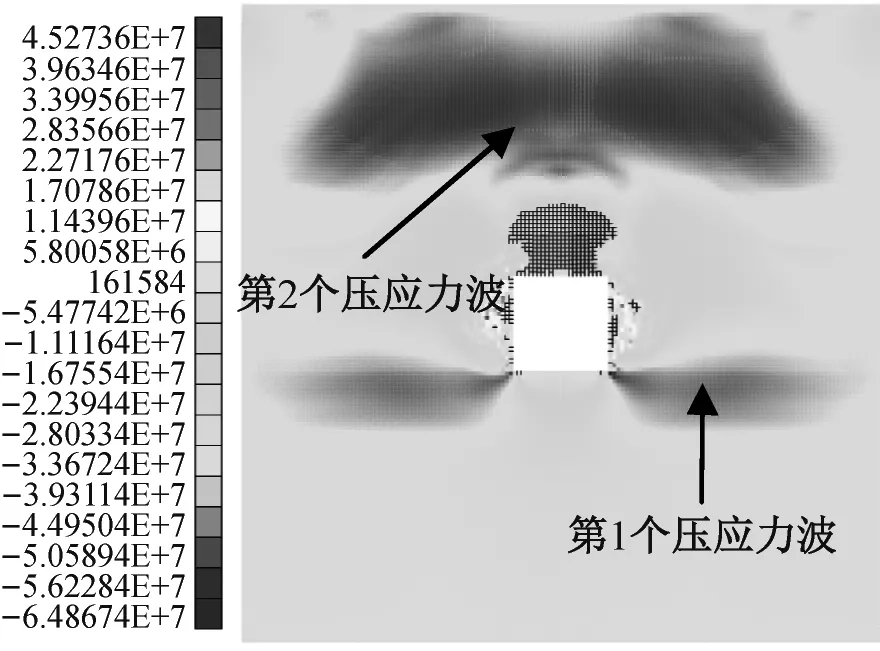
当N=20 000时(图6(a)和图7(a))，第1个压应力波开始传入洞室围岩；当N=21 500时(图6(n)和图7(f))，第1个压应力波开始传出洞室围岩。当N=20 700时(图6(f))，第1个压应力波波前抵达洞室顶板表面后分化为左、右两部分和中间部分。

当N=20 000～21 500时(图6(a)～图6(n)和图7(a)～图7(f))，第1个压应力波的中间部分在洞室顶板表面发生反射，洞室顶板产生了大量拉裂缝且逐渐增多；同时，第1个压应力波的左、右两部分向下继续传播，经过洞室两帮后，洞室两帮产生了拉、剪裂缝(剪裂缝最先产生在洞室的左、右上角(图7(b)))，拉裂缝逐渐增多，剪裂缝发展后形成V形坑且深度增加。当N=21 500～24 000时(图6(n)～图6(q)和图7(f)～图7(i))，拉、剪裂缝不断在两帮扩展，并向上发展，在原有V形坑之外形成V形坑。当N=24 000时(图6(q)和图7(i))，最后1个压应力波已完全传入洞室围岩。随后，洞室顶板和两帮的拉、剪裂缝有一定程度的扩展，部分脱离围岩的单元涌入洞室。当N=25 000时(图6(r)和图7(i))，与N=24 000时相比，洞室两帮的拉裂缝有所扩展，同时，洞室两帮的V形坑的上方产生了一些剪裂缝。

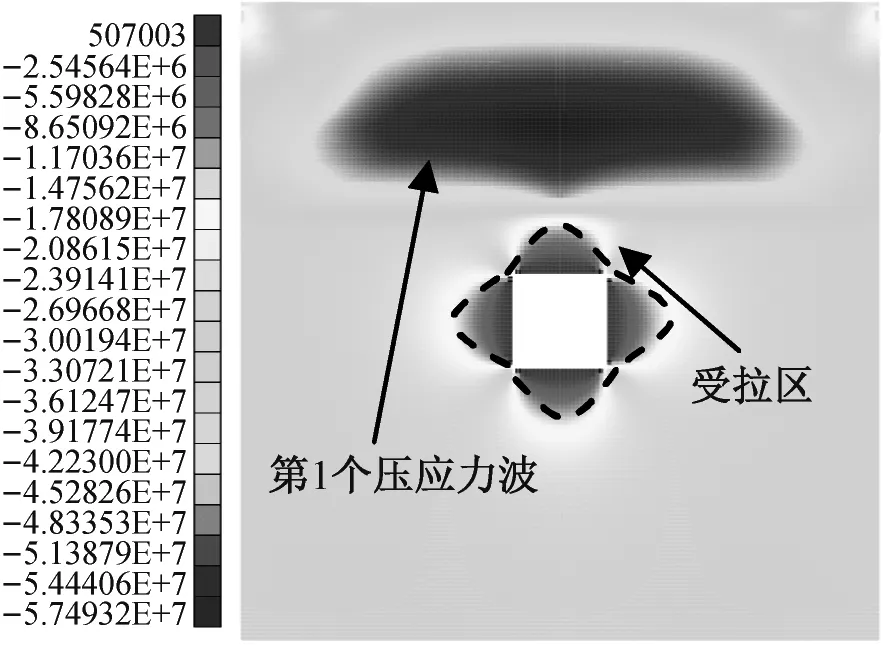
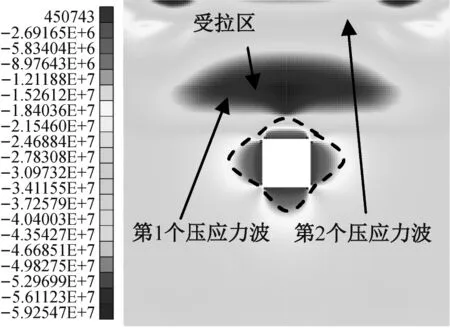
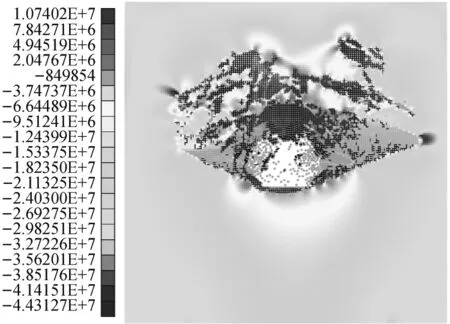
当N=25 000～45 000时(图6(r)～图6(s)和图7(i)～图7(k))，拉、剪裂缝的扩展基本停滞；洞室顶板的拉裂缝数目比两帮的多，这表明冲击下洞室顶板的破裂以拉裂为主；洞室两帮剪裂缝数目比顶板的多，这表明冲击下洞室两帮的破裂以剪裂为主。董锁堂[20]利用水泥类的膨胀胶凝材料与水反应体积骤增的特点对洞室围岩进行冲击实验，发现了洞室顶板和两帮均破坏，且两帮呈“V”形坑。在现场反复爆破下，洞室顶板和两帮发生破坏现象[21]也是常见的。当N=70 000时(图6(t)和图7(n))，1条裂缝由洞室右帮扩展至模型的上端面，这将导致洞室围岩的不平衡。

总体上看，洞室顶板的拉裂缝数目比洞室两帮的多，其范围比两帮的大，洞室两帮的剪裂缝数目比洞室顶板的多，其范围比顶板的大。

3.2.2 第1个压应力波冲击下拉、剪裂缝的时空分布

由上文结果可见，第1个压应力波造成了洞室围岩较严重的破裂。因此，下面以方案1为例，细致分析第1个压应力波的传播过程，简单涉及第2和3个压应力波。由图6(a)～图6(n)总体上可以发现：首先，随着第1个压应力波传入，洞室顶板的σ3受拉区逐渐被压缩，第1个压应力波与洞室四角的σ3受压区逐渐联通；然后，第1个压应力波的中间部分在洞室顶板发生反射，导致顶板拉裂；同时，第1个压应力波的左、右两部分向下传播，在经过洞室两帮后，两帮产生了少量拉裂缝。

(a) N=20 000

(b) N=20 050

(d) N=20 500

(e) N=20 600

(f) N=20 700

(g) N=20 800

(h) N=20 900

(i) N=21 000

(j) N=21 100

(k) N=21 200

(l) N=21 300

(m) N=21 400

(n) N=21 500

(o) N=22 000

(p) N=23 000

(q) N=24 000

(r) N=25 000

(s) N=45 000

t) N=70 000

首先，细致介绍图6中σ3和拉裂缝的时空分布。

当N=20 000时(图6(a))，洞室两帮及顶、底板各存在1个弓形的σ3受拉区，其深度约为2.9 m，洞室四角存在σ3受压区。应当指出，正方形洞室周边的环向应力σθ=αp+βλp[22]，式中，α和β为应力集中系数，其大小与位置有关，洞室四角处的α和β最大[23]；λ为侧压系数；p为原岩垂直应力。所以，洞室四角处的σθ最大。在冲击载荷施加之前且洞室开挖之后围岩平衡时，本文中洞室四角处存在σ3压应力集中与上述理论结果相符。此时，第1个压应力波刚传入洞室围岩。当N=20 050～20 500时(图6(b)～图6(d))，第1个压应力波逐渐传入洞室围岩，在模型的上端面附近，形成了1个σ3受压区。当N=20 500时(图6(d))，该压应力波波前已接近洞室顶板表面，其与洞室左、右上角的σ3受压区有联通趋势；洞室顶板的受拉区尺寸与过去相比减少，其深度约为2.8 m。

当N=20 600～20 900时(图6(e)～(h))，第1个压应力波波前抵达洞室顶板表面后分化为3部分，第2个压应力波波前抵达洞室顶板。第1个压应力波的中间部分在洞室顶板表面发生反射，反射的拉应力波导致顶板拉裂，同时，第1个压应力波的左、右两部分继续传播，与洞室左、右下角的σ3受压区逐渐联通。当N=20 600时(图6(e))，洞室顶板的σ3受拉区深度被压缩至约1.9 m。当N=20 700时(图6(f))，洞室顶板的σ3受拉区基本消失。N=20 800时(图6(g))，洞室顶板的σ3受拉区有所恢复。

当N=21 000～21 100时(图6(i)～图6(j))，第1个压应力波的左、右两部分波前抵达洞室底板后有汇合趋势；第2个压应力波波前接近洞室顶板的拉裂区；第3个压应力波传入洞室围岩。当第1个压应力波的左、右两部分经过洞室两帮之后，两帮首先出现了少量拉裂缝(图6(i))，然后拉裂缝有所扩展(图6(j))。

当N=21 200～21 500时(图6(k)～图6(n))，第1个压应力波已汇合，呈整体连续展布；第2个压应力波分化为3部分，左、右两部分波前经过洞室两帮抵达底板，两帮的拉裂缝有所扩展；第3个压应力波波前已接近洞室顶板的拉裂区。

然后，简单介绍图7中σ1和剪裂缝的时空分布。

当N=20 000时(图7(a))，洞室四角存在σ1受压区。当N=20 900时(图7(b))，第1个压应力波的左、右两部分抵达洞室两帮，并与洞室四角的σ1受压区联通，在洞室左、右上角产生了少量剪裂缝。当N=21 000时(图7(c))，洞室左、右上角的剪裂缝斜向下扩展，扩展后的剪裂缝与洞室左、右下角的联通，形成V形坑。当N=21 300时(图7(e))，剪裂缝和V形坑与此前的相比变化较小。当N=21 500时(图7(f))，洞室两帮的V形坑之外出现了一些剪裂缝，并有形成更大V形坑的趋势。

(a) N=20 000

(b) N=20 900

(d) N=21 100

(e) N=21 300

(f) N=21 500

(g) N=22 000

(h) N=23 000

(i) N=24 000

(j) N=25 000

(k) N=45 000

(l) N=70 000

总体上看，第1个压应力波的中间部分在洞室顶板表面发生反射之后，洞室顶板出现拉裂缝；第1个压应力波的左、右两部分经过洞室两帮之后，两帮出现拉、剪裂缝，其中，剪裂缝扩展后形成V形坑。

(a) N=20 000

(b) N=22 000

(d) N=25 000

(e) N=45 000

(f) N=70 000

(a) N=20 000

(b) N=22 000

(d) N=25 000

(e) N=45 000

(f) N=70 000

3.3 压应力波幅值的影响

首先，以方案1(Pmax最大)为例，介绍Nt和Ns随N的演化规律。

由图10可以发现，Nt-N曲线大致可被分为3个阶段：恒为0阶段、近似阶梯增长阶段和基本恒定不变阶段。

在恒为0阶段(N=20 000～20 872)，共有2个压应力波传入洞室围岩，其中，第1个压应力波波前尚未抵达洞室顶板表面。

在近似阶梯增长阶段(N=20 873～25 000)，在Nt-N曲线上隐约可见8个阶梯。每个阶梯可被分成快速增长部分和缓慢增长部分，分别对应于拉裂缝的快速扩展和缓慢扩展。在第1个阶梯阶段(N=20 873～21 419)，Nt首先快速增至964，然后，缓慢增长。这是因为第1个压应力波波前抵达洞室顶板表面后发生分化，中间部分反射造成洞室顶板拉裂，左、右两部分向下传播造成洞室两帮拉裂。在此阶段，第2个压应力波对洞室围岩的影响不显著。在最后1个阶梯阶段(N=24 181～25 000)，Nt首先由2 670快速增至4 202，然后，基本保持不变。应当指出，前7个压应力波分化的中间部分反射后的拉应力波将分别与后继的压应力波叠加，这将导致拉应力波的幅值降低，而最后1个压应力波分化的中间部分反射后，拉应力波附近不再有压应力波，所以将造成更严重顶板的拉裂。

在基本恒定不变阶段(N=25 001～30 000)，Nt基本为4 206。在此阶段，洞室围岩正在形成某种有利于平衡的结构，应力在调整之中。应当指出，当N>30 000时，本文未统计Nt和Ns，这是因为最后1个压应力波在N≈26 100时完全传出模型，之后洞室围岩的裂缝扩展与由模型上端面传入的压应力波不应该有关系；当N=70 000时(图6(t))，拉裂缝扩展至模型上端面，应力调整失败，洞室围岩不平衡。

由图10和图11可以发现，Ns的演化规律与Nt的有相似之处，例如，在近似阶梯增长阶段，隐约可见8个阶梯。二者的演化规律亦有所不同：Ns突增较少，在第1和第8阶梯阶段，其分别由0突增至363和由2 884突增至2 988。

然后，简单介绍方案3(Pmax较小)的Nt和Ns随N的演化规律。

Nt-N曲线和Ns-N曲线的形式基本相同，大致可被分为4个阶段：恒为0阶段、快速增长阶段、缓慢增长阶段和基本恒定不变阶段。

在快速增长阶段和缓慢增长阶段，Nt首先快速增至350(N=20 873～20 893)，这是因为第1个压应力波分化的中间部分反射后造成了洞室顶板拉裂，然后，缓慢增至615(图8(b)～图8(d))；Ns首先快速增至27(N=20 825～20 855)，这是因为第1个压应力波分化的左、右两部分造成了洞室左、右上角剪裂，然后，缓慢增至137(图9(b)～图9(d))。

在基本恒定不变阶段(N=25 001～30 000)，Nt和Ns分别为615和138。应当指出，当N>30 000时，拉、剪裂缝的扩展停滞(图8(e)～图8(f)和图9(e)～图9(f))，洞室围岩平衡。

最后，对方案1和方案3的结果进行简短对比。

由图10和图11可以发现，在相同N时，方案3的Nt和Ns均小于方案1的，这是因为Pmax越小，洞室围岩受到的冲击作用越小，因而拉裂和剪裂越不显著。这与文献[9]中冲击下洞室围岩模型拉、剪裂缝数目与应力波幅值成正比的结果有类似之处。该文献采用颗粒流软件进行模拟，只给出了拉、剪裂缝数目的一个特定时刻的结果，而本文给出的是二者的演化过程。

图10 方案1～方案4的拉裂缝区段数目-N曲线

图11 方案1～方案4的剪裂缝区段数目-N曲线

由图7～图9可以发现，随着Pmax的减小，洞室两帮的V形坑最大深度减小，例如，当N=24 000时，方案1的约为12 m，方案3的约为2 m；当N=25 000时，方案1的约为14 m，方案3的约为3 m。

文献[24]将冲击地压强度分成1～5级：微弱、较弱、较强、强烈和极强烈。冲击地压强度为1级时，围岩发生极少量片帮、掉渣和冒顶等现象；冲击地压强度为4级时，围岩发生较严重破坏，巷道断面收缩超过1/2。在济三煤矿，1级和4级冲击地压多有发生[25]。显然，方案1的模拟结果(例如，洞室顶板和两帮出现大量裂缝，大量脱离围岩的单元涌入洞室并堆积在底板(图6(s)～图6(t))与4级冲击地压特征相一致，而方案3的模拟结果(例如，洞室顶板和两帮出现少量裂缝，极少量脱离围岩的单元涌入洞室(图8(e)～图8(f)))与1级冲击地压特征相一致。

4 讨论

4.1 顶板拉裂机理

众所周知，当若干应力波在模型中传播时，遇到无透射边界将发生反射和叠加，压应力波反射为拉应力波。在洞室围岩的某一位置，当压应力波传播到时，岩石将受强烈挤压作用；当压应力波经过该位置后，岩石的受压程度降低，甚至将受拉作用，即σ3>0。当无透射边界反射的拉应力波与该位置的大于0的σ3发生叠加或只有拉应力波作用时，都可能造成拉裂。下面，以方案1为例进行阐述。当N=20 700时(图6(f))，第1个压应力波已抵达洞室顶板表面，分化为3部分，其中，中间部分在洞室顶板表面发生反射，此时，洞室顶板附近σ3<0，受压。当N=20 800时(图6(g))，洞室顶板附近σ3>0，受拉，这显然是由压应力波的反射造成的；在第1与第2个压应力波之间的某些位置，σ3较高，受压程度不强烈甚至受拉。当N=20 900时(图6(h))，在洞室顶板，反射的拉应力波单独自己或与两压应力波之间的较高的σ3叠加，造成了拉裂。总之，冲击下洞室顶板的应力波反射或叠加导致拉裂。

文献[9]将冲击载荷简化为一个简谐波，采用PFC2D研究了冲击载荷幅值对拱形巷道围岩的应力场、位移场及破坏区的影响，并简单介绍了巷道顶板拉裂机理。本文与文献[9]的洞室外形和侧压系数等不同(例如，在冲击之前文献[9]的侧压系数为0.4，而本文为1)，本文洞室顶板的拉应力应该不如文献[9]的大，因此得到的洞室顶板拉裂机理与文献[9]的应该有所不同。本文的结果表明，在第1个压应力波向下传播时，顶板的受拉区被不断压缩，该压应力波反射后的拉应力波单独自己或与第1和第2个压应力波之间的受拉区叠加导致顶板拉裂，而文献[9]强调的是反射的拉应力波与洞室顶、底板及两帮附近的拉应力区叠加导致顶板拉裂。

4.2 裂缝对于应力波传播的吸能作用

众所周知，应力波的传播受材料性能的影响。当应力波经过软弱层时，应力波的能量消耗较大，对应力波的传播具有阻碍作用。顶板拉裂区对应力波传播的吸能作用在图6(n)～图6(q)中可以得到一定程度的体现。在N=20 900时(图6(h))，第1个压应力波分化后的中间部分造成的顶板拉裂区高度约为4 m。此后，一直到N=24 000时(图6(q))，该高度几乎保持不变。

4.3 洞室两帮拉、剪裂相伴现象

由图6和图7可以观察到洞室两帮拉、剪裂缝相伴现象，即剪裂位置及附近同时也发生拉裂。造成该现象的原因可以解释如下。当压应力波分化后的左、右两部分传播至洞室两帮时，两帮的σ1值快速增加。假定σ3变化不大，则σ1与σ3的差值将快速升高。当两帮的应力状态满足莫尔-库仑准则时，将形成V形坑。由于剪裂缝将围岩与V形坑内部的岩块隔离开来，V形坑内部的应力处于低值，甚至接近于零。上文已指出，压应力波波后存在一个挤压不强烈区甚至受拉区。所以，压应力波通过两帮后将造成V形坑位置拉裂，进而导致洞室两帮拉、剪裂相伴现象。