基于BOX-COX变换的桥梁结构地震易损性分析
2021-01-18张鹏辉郭军军周连绪袁万城
张鹏辉, 郭军军, 周连绪, 袁万城
(土木工程防灾国家重点实验室(同济大学), 上海 200092)
理论易损性曲线作为确定桥梁结构潜在地震风险的重要工具,建立了地震动强度指标(Intensity Measure, IM)与结构在某一损伤极限状态(Limit State, LS)下失效概率之间的联系[1],而云图法由于其计算效率上的优越性已经成为获取结构理论易损性曲线的主要途径之一[2-3]。然而以往的研究发现云图法在建立概率地震需求模型(Probabilistic Seismic Demand Model, PSDM)时,为简化计算所作出的三个基本假设常常与现实相违背,存在以下三个问题,即:(1) 特定地震动强度水平下的工程需求参数(Engineering Demand Parameter, EDP)不服从对数正态分布;(2) ln(IM)与ln(EDP)间不满足线性相关;(3) ln(EDP)的方差随IM取值变化[4-6]。Karamlou等[5]考虑结构不确定性,通过大量数值模拟研究了上述三个问题对理论易损性曲线计算结果的影响,研究表明与问题(1)相比后两者对易损性曲线计算结果的影响更严重。为改善问题(2),Padgett等[7]考虑高效性、实用性、充分性以及灾害的可计算性对IM的选取进行优化,Pan等[8]采用二次函数对ln(IM)与ln(EDP)进行回归,Mackie等[9]采用双线性函数对ln(IM)与ln(EDP)进行回归,均取得了较好的效果。此外,为了避免云图法三个基本假设对易损性曲线计算结果的影响,研究人员通过增量动力分析(Incremental Dynamic Analysis, IDA)方法获取易损性曲线,但该方法存在对地震动时程的放缩且需要的时程分析次数剧增等问题,故应用受到限制[10]。如何改进理论易损性分析方法,使其能够不受上述三个基本假设的限制,同时又不增加时程分析次数是当前理论易损性分析亟待解决的问题。
本文旨在不显著增加计算量的前提下提高易损性分析结果的可靠性,通过引入BOX-COX变换使概率地震需求模型满足对数正态分布、线性和同方差性假设,结合蒙特卡洛抽样得到结构易损性曲线,并以一座三跨连续梁桥为例,验证该方法的有效性。
1 基于BOX-COX变换的地震易损性分析方法
1.1 云图法的基本假设和BOX-COX变换
Cornell等[11]假设EDP的均值(SD)与IM之间满足对数线性关系,并建立普通最小二乘(Ordinary Least Square, OLS)回归模型
(1)
式中,α1、α2均为回归系数。因此式(1)需服从OLS回归中的对e作出的正态性和同方差性假设,由此得到概率地震需求模型
(2)
式中:D为构件的需求;Φ(·)为标准正态分布函数;βD为构件需求的对数标准差。
(3)
若进一步假定构件在某一损伤极限状态(LSj)的抗震能力C服从均值为SC对数标准差为βC的对数正态分布,则云图法得到的构件在LSj下的失效概率为
(4)
由此可见,云图法中所作的三个基本假设,本质是为OLS回归模型式(1)服务的。当ln(SD)与ln(IM)之间关系非线性,或回归的残差e不再服从正态性和同方差假设时,回归系数α1、α2的估计不再是最小方差线性无偏估计,式(1)的应用效果将不理想,进而影响构件易损性计算的可靠性[12]。
BOX-COX变换由Box等[13]提出,在回归分析领域应用广泛,通过对因变量y=ln(EDP)进行适当的变换,可在不丢失任何信息的前提下,使回归模型满足线性、正态性和同方差假设
(5)
其中a为使y+a的各个分量都大于0的系数,当min(y)>0时a=0;当min(y)≤0时a=roundup(|min(y)|),roundup(·)为向上取整函数[14]。引入BOX-COX变换后,式(1)更新为BOX-COX回归模型
(6)

(7)
记x=ln(IM),那么y=(y1,y2,…,yn)的联合概率密度函数可表示为
f(y)=

(8)
对式(8)两边取对数可得极大似然函数

(9)
考虑到式(9)求偏导较为困难,无法得到λ的解析解,因此本文以0.01作为搜索步长,找到使L(λ)达到最大值的λ作为其数值最优解。
1.2 基于BOX-COX变换和蒙特卡洛抽样的地震易损性分析

(10)
则构件在LSj下的失效概率为
(11)
值得指出的是,由于蒙特卡洛抽样所增加的计算时间是有限的,相较于时程分析来说可忽略不计。
2 算例分析
2.1 有限元模型
本文以一座预应力混凝土连续梁桥为例,如图1所示。跨径布置为60 m+100 m+60 m,主梁采用C50混凝土的预应力箱梁;支座为球钢支座,支座布置如图1所示。滑动支座摩擦因数取0.02,屈服位移取2 mm[17],屈服力为最大静摩擦力;桥墩采用C40混凝土,钢筋种类为HRB335,纵向钢筋配筋率0.8%,体积配箍率1%;以梅花形布置的直径2 m钻孔灌注桩作为基础;两侧桥台均为桩接盖梁桥台。使用OpenSees程序建立全桥非线性有限元模型(如图2)。主梁采用弹性梁柱单元模拟;桥墩采用弹塑性纤维单元模拟,混凝土本构采用Kent-Park-Scott模型[18],不考虑混凝土的抗拉性能,钢筋采用考虑强化的双线性本构。支座、桩基、碰撞均采用零长单元模拟,采用M法计算土弹簧六个方向的刚度,碰撞单元采用Muthukumar提出的本构模型[19],伸缩缝采用碰撞单元模拟,碰撞单元的初始缝隙根据桥台处伸缩缝缝宽取为15 cm。由于桥台对构件的地震响应有显著影响[20],本文参考Nielson给出的桥台模拟方法[21],被动土压力方向的刚度由桩基和桥台共同提供,主动土压力方向刚度仅由桩基提供,以零长单元进行模拟。

图1 桥梁结构总体布置图(m)

图2 有限元模型示意图
2.2 地震动时程
地震动时程的选取是易损性分析的关键之一,Baker等[22]提出的非条件谱选波方法能够根据地震动预测模型(Ground Motion Prediction Model, GMPM)得到的场地均值谱和方差选取符合目标反应谱概率分布的一组波。采用该选波方法,首先按焦驰宇[23]给出的中美剪切波速换算公式得到Ⅲ类场地30 m深度范围内的土层平均剪切波速V30;然后根据Boore等[24]提出的地震动预测模型生成适用于中国区域震级M=7,断层距Rjb=15 km,V30=205 m/s的反应谱概率分布;最后从NGA-West2强震数据库中按M=6~8,Rjb=0~100 km,V30=150~260 m/s选出100条符合目标反应谱分布的原场单向地震动分量。图3画出了它们的加速度反应谱,图4给出了这些地震动时程的震级和震源距分布直方图。将这100条地震动时程按纵桥向输入,得到结构各构件的响应。

图3 地震波的加速度反应谱(阻尼比5%)

图4 震级和震源距分布直方图
2.3 概率地震需求模型建立与比较
Riddell[25]指出对于短周期结构选用加速度相关型的地震动强度指标(IM)是合适的,Moschonas等[26-27]采用PGA(Peak Ground Acceleration)作为IM对一系列中小跨径梁桥和大跨度钢构桥进行易损性分析,并取得了较好的效果。本文模型桥一阶周期0.95 s,结构周期较短;同时PGA的地震危险性曲线目前已经能够得到,即具有良好的灾害可计算性,而结构相关型的地震动强度指标Sa(T1)的地震危险性曲线目前还未给出,故选用PGA(单位:g)作为地震动强度指标。连续梁桥的易损部位为桥台、支座和墩柱,故选用被动土压力方向桥台位移δp、主动土压力方向桥台位移δa、滑动支座位移δb、固定墩墩顶漂移率Dr作为工程需求参数[28]。将时程分析结果,分别按式(1)和式(6)进行OLS回归和BOX-COX回归得到概率地震需求模型。
为评价残差e的正态性,作出回归残差的频率分布直方图并得到其核密度估计与按正态分布拟合的概率密度函数,核密度估计曲线(Kernel Density Estimation Curve, KDE)与正态分布概率密度曲线(Norm)的偏差情况反映了残差e的分布与正态分布的偏离程度。自变量与因变量的线性相关性强弱通过回归决定系数(R2)来衡量,它是两变量线性相关系数的平方。异方差性的诊断采用等级相关系数法,计算等级相关系数(rs)首先需要对回归模型(1)和(6)中的自变量xi和残差绝对值|ei|分别进行排序,则
(12)
其中di对应于xi和|ei|等级的差数。对rs进行显著性检验得显著性水平p,一般认为p<0.05时认为回归模型存在异方差性。表1列出了OLS回归和BOX-COX回归的结果。

表1 OLS回归和BOX-COX回归的结果
由表1结果可知,当以δp、δa和δb作为EDP建立概率地震需求模型时,均存在显著的异方差性,通过BOX-COX变换后,异方差问题得到消除。同时BOX-COX回归的决定系数较OLS回归平均提升了3.26%,δp的决定系数增加达到8.2%,说明自变量和因变量的线性相关程度有所提高。为直观显示残差的非正态和异方差问题,图5作出了δp回归残差的分布图和频率分布直方图以及KDE曲线和Norm曲线。由图像可看出OLS回归的残差在PGA较小时方差较小,随着PGA的增大逐渐增加,即OLS回归将方差作为一个定值过程中在PGA较小时对方差进行了高估,在PGA较大时低估了方差,且残差的分布与正态分布具有一定程度的偏离,进行BOX-COX变换后,残差的正态性得到改善,对δa和δb分析所得结果相同。需要说明的是,当应用云图法以Dr作为EDP时,检验结果发现其概率地震需求模型满足自身的三个基本假设。

(a) 基于OLS回归的PSDM

(b) OLS回归残差图

(c) 基于BOX-COX回归的PSDM
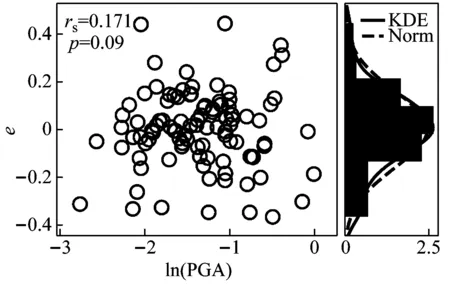
(d) BOX-COX回归残差图
2.4 构件易损性曲线比较
Hwang等[29]建议将桥梁的损伤描述为四个极限状态,即轻微损伤(LS1)、中等损伤(LS2)、严重损伤(LS3)、完全损伤(LS4)。参考前人的研究结果,对应不同损伤极限状态,本文采用的能力均值和对数标准差见表2。

表2 不同损伤极限状态的能力均值和标准差
根据式(11)可求得各构件在不同损伤极限状态下的易损性曲线,并与云图法得到的构件易损性曲线进行比较,如图6所示。由图6(a)~6(c)可知,因为OLS回归在PGA较小时高估了方差,导致在该PGA范围内云图法得到的失效概率偏大,最大偏差2.21%;而当PGA较大时OLS回归低估了方差,故云图法得到的失效概率偏小,最大偏差27.2%。且极限状态对应的损伤程度越高,采用云图法得到该极限状态下的易损性曲线偏离实际越明显。当PGA=1g时,δp达到LS3状态、δa达到LS2状态的和δb达到LS2状态的概率分别被低估18.1%、524.7%、30.9%,若仍然采用云图法的三个基本假设,将导致易损性计算结果失真。由图6(d)可知,当采用云图法能够满足自身基本假设时,基于BOX-COX变换的易损性分析方法(采用BOX-COX回归建立需求模型)所得易损性曲线与云图法(采用OLS回归建立需求模型)计算结果相同,即BOX-COX变换不会导致信息的丢失。
3 结 论
(1) 提出了结合BOX-COX变换和蒙特卡洛抽样的地震易损性分析方法,消除由于云图法的三个基本假设带来的易损性计算误差,并通过算例验证了其应用于连续梁桥地震易损性分析的有效性。


(a) 被动土压力方向桥台位移

(b) 主动土压力方向桥台位移

(c) 滑动支座位移
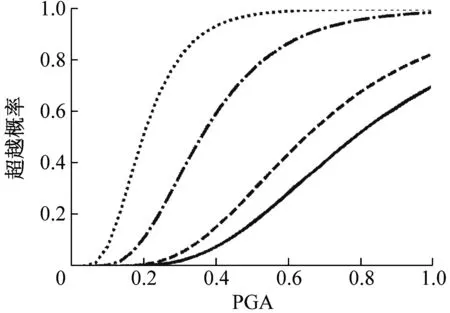
(d) 固定墩墩顶漂移率
(2) 采用BOX-COX变换建立的概率地震需求模型,无须遵循云图法所特有的三个基本假设,且改善了云图法特有的三个基本假设带来的易损性计算误差,使模型的线性程度提高,正态性改善,异方差性消除;同时,保持了云图法非线性时程分析次数少的优点。
(3) 在云图法适用的情况下,采用本文提出的方法计算的易损性曲线与云图法结果一致;当概率地震需求模型存在异方差性时,使用云图法将导致结构易损性曲线计算结果的失真,且极限状态对应的损伤程度越高,该极限状态下的易损性曲线偏离实际越明显。
