初中数学辅助线生成的教学实践与思考

高海军

摘  要：初中数学几何推理是学生的薄弱环节，而有些几何题需要添加辅助线，才能使题目中的隐含条件显性化，学生才能推理顺畅。添加辅助线是求解几何题的常用方法，也是思维生成的难点和盲区。为了突破思维生成的难点，教师注重在题量和解题技巧上下功夫，供学生模仿理解，但是效果甚微。从浅层次来看，学生不能理解数学的本质，不能内化为自己的思维;从深层次来看，教师要培养学生学会思考，要善于借助转化思想剖析辅助线生成的本质，提升学生分析问题和解决问题的能力。

关键词：课后习题;辅助线;转化思想;教学实践

在数学教学实践中，有很多几何题不能直接反映题目所给条件与结论之间的关系，常常需要添加辅助线构成新图形，需要把分散条件集中化，隐性条件显性化，在已知与未知之间架起桥梁，将不熟悉的几何图形转化为熟悉的几何图形加以解决。学生要明确如何添辅助线，为什么添加，有什么作用，这是解决问题的关键。如果能培养学生借助转化思想，把不熟悉的知识转化为熟悉的知识，深入思考辅助线生成的本质，就可以找到解决问题的本源，有效突破难点。

一、原题呈现

人教版《义务教育教科书·数学》八年级下册第十八章“平行四边形”复习题第14题如下。

如图1，四边形ABCD是正方形，点E是边BC的中点，∠AEF = 90°，且EF交正方形外角的平分线CF于点F。求证：AE = EF。（提示：取AB的中点G，连接EG。）

此题是学生在掌握了第十八章全部内容以后，进行单元复习课时遇到的拓广探索题。从内容上看，此题涉及面广，以正方形为主要背景知识，考查全等三角形的性质与判定定理，以及等腰三角形、直角三角形的基础知识;从解题方法上看，主要考查全等三角形的应用，通过角与线段的迁移，恰当添加辅助线，寻找桥梁，把已有条件和目标线段联系起来，从而解决问题。但是，在实际教学中，这道题很多学生几乎不会做，无从下手。笔者将教学策略分享于此，仅供参考。

二、解决策略

思考1：如何证明AE = EF？利用隐藏条件构建这两条线段所在的三角形全等。

方法1：引导学生分析除了已给的条件外，能发现几何图形中还有哪些隐藏条件。不难发现，利用同角的余角相等，可得∠1 = ∠2。因为点E是BC的中点，所以用添加辅助线的方法取AB的中点G，连接EG，如图2所示。由条件可证AG = EC，∠AGE = ∠ECF = 135°，依据“ASA”定理易证明△AGE ≌ △ECF，从而得到AE = EF。

【反思】构建∠1 = ∠2，AE = EF的全等三角形是关键。结合图形，只能取AB的中点G，作辅助线连接GE，把隐性问题显现出来。

方法2：如图3，连接AC，结合图形已有条件，引导学生分析还有哪些隐性条件。不难发现，利用等角的余角相等可得∠1 = ∠EFC。因为点E是BC的中点，所以添加辅助线，可以过点E作GE⊥BC，垂足为点E，交AC于点G，构造△AGE和△ECF全等。根据条件，学生容易证明∠1 = ∠EFC，∠2 = ∠3，GE = CE，依据“AAS”易证明△AGE ≌ △ECF，从而证明得出AE = EF。

【反思】合理添加辅助线，构造△AGE和△ECF全等，是解决问题的关键。

思考2：如何证明AE = EF？利用轴对称变换构建等腰三角形。

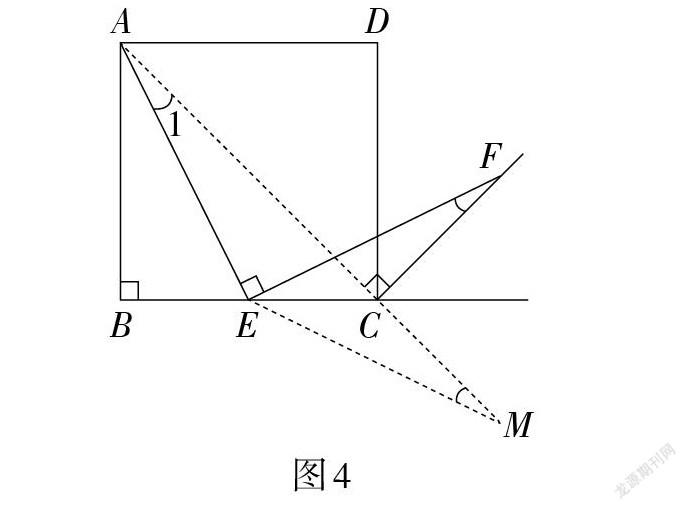
方法3：由于直接证明AE = EF相等的条件不具备，则可以利用轴对称变换的转化思想，使△ECF ≌ △ECM。因此，构建如图4所示的辅助线，连接AC并延长到点M，使CM = CF，连接EM。依据条件易证明∠1 = ∠EFC，利用“SAS”证明△ECF ≌ △ECM，可得EF = EM，∠EFC = ∠M，推得∠1 = ∠M，所以AE = EM，最后可证明AE = EF。

【反思】利用等角对等边和轴对称的基本性质，恰当、合理添加辅助线，帮助学生转化思维，形成合情合理的逻辑推理。

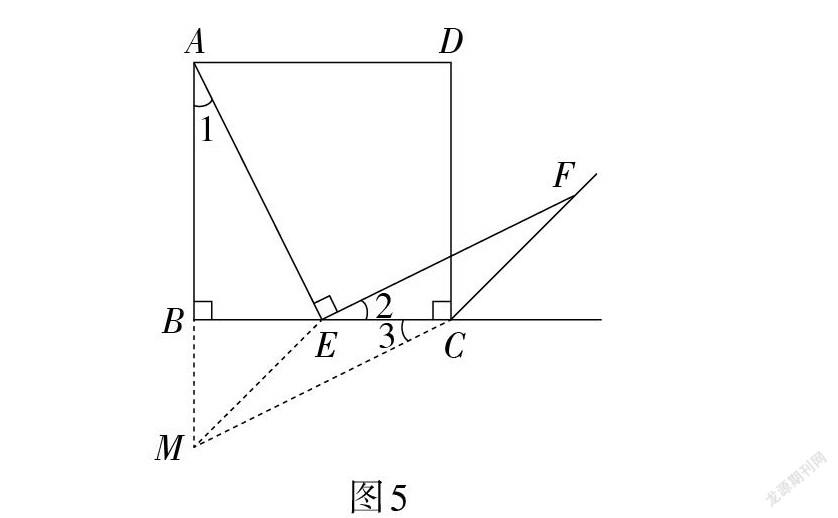
方法4：如何证明AE = EF？进一步引导学生深入思考，利用旋转变换构建全等三角形。以点B为中心，将△ABE顺时针旋转90°，连接EM，如图5所示。由旋转可得△ABE ≌ △CBM，可得AE = CM，BE = BM，∠1 = ∠3。因为∠MBE = 90°，所以∠BEM = 45°;因为∠1 = ∠2，所以∠2 = ∠3，所以EF∥MC。由∠BEM = 45°可得∠MEC = ∠ECF = 135°，所以ME∥CF，所以四边形EMCF是平行四边形，所以EF = CM，所以AE = EF。

【反思】利用旋转和平行四边形的性质添加辅助线，帮助学生构建熟悉的几何图形模型是解题的核心，能够体现学生综合运用所学知识解决问题的综合能力。

三、教学实践

从这道题的不同解法可以发现，之所以学生对这种问题掌握不扎实、理解不到位，一是因为学生对知识的迁移和内在转化不到位;二是教师在平时的教学中，只注重教学方法，不注重学习方法;三是学生在平时的学习中，不善于思考、反思和总结，只重结果，不重过程。添加辅助线，把隐含条件显性化，对于八年级学生来说本身就是一个难点。学生对此种方法的理解是一个螺旋上升的过程，教师要遵循学生的认知规律和教学规律，扎实有效地推进教学。

1. 单元知识整体融合

此题融合了三角形、轴对称、旋转、平行四边形的重要知识。在单元复习课中，教师如果深入挖掘和研究题目，则可以从不同角度帮助学生复习整章知识，而且还可以提升学生分析问题和解决问题的能力。因此，在上单元复习课时，教师要认真备课，了解学情，深入挖掘教材复习题中蕴含的各章节知识点，使其融合，提高知识容量，做到精讲精练，提高课堂效率。

2. 开展深度教学

此类问题在教材上涉及少，但是中考中时常出现，考查学生的数学思维品质。教师要把此类问题简单化、一般化，深入浅出，总结方法，才能激活学生的认知思维，提高课堂效率。但是，在实际教学中，课堂教学有时往往是浅层的教学活动，表现出来的是教师一讲会，但学生一做不会，本质是学生未能真正掌握问题的实质和根源。为了避免这种课堂现象的出现，就必须要深度教学，离不开教师深入研究教材、研究教学方法，挖掘题目本源，也离不开教师精心地组织引导学生深度思考。因此，教师要认真备课、深度备题，做到心中有数，也必须克服教学过程中表面、表层、表演的局限，引导学生深层、深刻、深度思考，经历从理论到实践的一整套思维方式和行为模式的转化和训练，深度教学才能促进深度学习的真实发生。

3. 落实实践教学

实践教学尤为重要。在平时的教学中，教师要精讲精练，给予学生思考的时间，尝试一道题用不同的解法。不同的学生有不一样的思维模式，有复杂的、简单的，教师要学会分析不同方法，引导学生选择最优的解题思路，并不断自我总结和反思，这样才能内化为学生自己的知识，提升学生分析问题和解决问题的能力。

四、深度思考

如图6，当点E在BC上（点B，C除外），其他条件不变，上面的结论是否仍然成立呢？试从“点E在BC上”“点E在BC延长线上”“点E在BC的反向延长线上”三种情况中任选一种情况，画出图形并证明你的结论。此题的变式就是激活学生的思维应变能力，如果前面提到的四种方法学生都能掌握，那么这道变式题就不会有很大困难。

【设计意图】此题主要是让学生深度思考，进一步体会运用从特殊到一般的数学思想，考查学生分析问题和解决问题的综合能力。

五、结束语

授之以鱼，不如授之以渔。在数学教学过程中，教师要善于一题多解，激活学生的思维，使每名学生都有不同的收獲。添加辅助线的方法不是固定的，除了关注题目中的显性条件外，还要挖掘题目中的隐性条件，通过合理添加辅助线，大胆进行思维关联与尝试，从而提升思维素养，发挥学生的创造性思维，这样才能做到课堂教学高效率，学生学习高成效，教学难点才能真正实现突破。

参考文献：

[1]张雄，李德虎. 数学方法论与解题研究（第二版）[M]. 北京：高等教育出版社，2018.

[2]朱毅航. 初中数学几何证明题的解题思维培养路径探析[J]. 理科考试研究（初中版），2016，23（3）.