r-特殊首尾和循环矩阵的行列式及其逆矩阵的算法
2021-01-12曾慧程
曾慧程,蔡 静
(湖州师范学院 理学院, 浙江 湖州 313000)
0 引 言
循环矩阵作为一类特殊矩阵被广泛应用于图象处理、编码理论、线性预测等方面[1-3].很多学者对其进行了研究和推广,并提出了许多特殊的循环矩阵.首尾和循环矩阵就是其中一类,在纠错码理论中频繁出现.2003年,黄德超等[4]提出了首尾和循环矩阵求逆的快速算法;同年江兆林[5]提出了首尾和r-循环矩阵及首尾和r-向后循环矩阵的概念.相比首尾和循环矩阵,首尾和r-循环矩阵出现了参数r,结构更为特殊.2004年,朱泉涌等[6]提出了r-首尾和循环矩阵的新概念,并运用多项式矩阵理论计算了该矩阵的逆;2016年,师白娟[7]在r-首尾和循环矩阵的基础上,研究了包含切比雪夫多项式的循环矩阵行列式的计算.关于首尾和循环矩阵的研究已较充分,但对r-首尾和循环矩阵的研究还相对较少.本文在r-首尾和循环矩阵的基础上,提出一种特殊的r-首尾和循环矩阵(记为SFLSCM),并运用多项式理论给出其行列式、逆矩阵或群逆的有效算法.
1 预备知识
定义1 若矩阵A∈n×n有如下形状:
则称A为r-特殊首尾和循环矩阵,记A=SFLSCr(a1,a2,…,an)∈SFLSCM.
本文定义如下矩阵Δ作为基本r-特殊首尾和循环矩阵:
(1)
易知g(x)=xn-r(xn-1+1)是矩阵Δ的特征多项式.此外,根据基本r-特殊首尾和循环矩阵的结构,可以得到Δn=r(Δn-1+E).
定义2[8]若矩阵A∈n×n,称满足rank(Ak+1)=rank(Ak)的最小非负整数k为矩阵A的指标,记作ind(A)=k.
定义3[9]若A∈n×n,ind(A)=k,如果n阶方阵X满足AkXA=Ak,XAX=X,AX=XA,则称X是A的Drazin逆;当ind(A)=1时,Drazin逆又称为群逆.
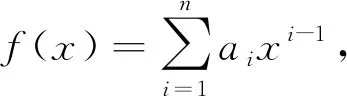
证明设
ωi是g(x)=xn-r(xn-1+1)的n个不同的根,则有:
所以矩阵V(ω1,ω2,…,ωn)是一个非奇异矩阵.

所以
AV(ω1,ω2,…,ωn)=V(ω1,ω2,…,ωn)diag(f(ω1),f(ω2),…,f(ωn)),
V(ω1,ω2,…,ωn)-1AV(ω1,ω2,…,ωn)=diag(f(ω1),f(ω2),…,f(ωn)),
即证得A的特征值为f(ωi),i=1,2,…,n.
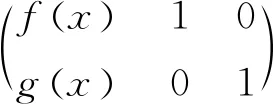
则(f(x),g(x))=d(x),且满足f(x)·u(x)+g(x)·v(x)=d(x).
2 主要结论




有:
所以
a1E+a2Δ+a3Δ2+…+anΔn-1=A,
即f(Δ)=A.
反之,A=f(Δ)=a1E+a2Δ+a3Δ2+…+anΔn-1=SFLSCM(a1,a2,…,an)∈SFLSCM.
定理3 若A,B∈SFLSCM,则AB=BA∈SFLSCM.
证明根据定理2,有:
A=f(Δ),B=u(Δ),
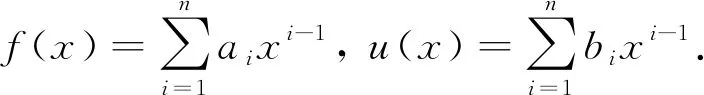
故有:
要证AB=BA∈SFLSCM,应先证明:AΔ=ΔA当且仅当A∈SFLSCM.
必要性显然成立,充分性证明如下:


由AΔ=ΔA得:
ai1=rai-1,n,i=2,3,…,n,
ain=ai-1,n-1+rai-1,n,i=2,3,…,n,
aij=ai-1,j-1,i=2,3,…,n,j=2,3,…,n-1.
故有:
所以A∈SFLSCM.
下证AB=BA∈SFLSCM.
因为A,B∈SFLSCM,所以AΔ=ΔA,BΔ=ΔB.故有:
ABΔ=AΔB=ΔAB,BAΔ=BΔA=ΔBA.
即证得.
定理4A∈SFLSCM,矩阵A可逆的充要条件是矩阵A的特征根f(ωi)≠0,i=1,2,…,n.
证明由定理1知:
因为矩阵A可逆,所以
故有f(ωi)≠0,i=1,2,…,n;反之亦成立.
定理5A∈SFLSCM,矩阵A可逆的充要条件是(f(x),g(x))=1,其中g(x)同引理1.
证明因为矩阵A可逆,所以f(ωi)≠0,又g(ωi)=0,故f(x)与g(x)无相同零点,即证得(f(x),g(x))=1;反之,若(f(x),g(x))=1,则存在u(x),v(x),使得u(x)f(x)+v(x)g(x)=1.由于f(Δ)=A,g(Δ)=0,则有u(Δ)A=E.因此矩阵A可逆且A-1=u(Δ),由定理2可得A-1∈SFLSCM.
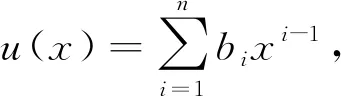
证明由引理2可得:
f(x)·u(x)+g(x)·v(x)=d(x),
因为矩阵A非奇异,由定理5可得:(f(x),g(x))=1,即d(x)=1.所以
f(x)·u(x)+g(x)·v(x)=1.
当x=Δ时,f(Δ)=A,g(Δ)=0,故有Au(Δ)=E.
令B=u(Δ),由定理2得B∈SFLSCM.显然B是唯一的,故得证.

证明由引理2可得:
f(x)·u(x)+g(x)·v(x)=d(x), ∂d(x)>0.
令
f(x)=f′(x)d(x),g(x)=g′(x)d(x),
则有:
(f′(x),g′(x))=1, (d(x),g′(x))=1,
根据多项式性质得:
(f(x)d(x)d(x),g(x))=1,
即(f(x)d(x),g′(x))=1.
因此,根据行初等变换有:
f(x)d(x)u(x)+g′(x)v(x)=1.
(2)
在式(2)右边同乘f(x),令x=Δ,C=d(Δ)u(Δ),整理得:
ACA=A.
(3)
在式(2)左边同乘d(x)u(x),整理得:
CAC=C.
(4)
因为C∈SFLSCM,根据定理3得AC=CA,满足定义3,故C是A的群逆.
下证唯一性.
若C不是A唯一的群逆,则设存在C′∈SFLSCM,使得
AC′A=A,C′AC′=C′,AC′=C′A.
(5)
故有:
C=CAC=CAC′AC=CC′AAC=C′ACAC=C′AC=C′AC′AC=C′AC′=C′.
即证得.
3 求逆算法
根据定理6和定理7获得求解r-特殊首尾和循环矩阵逆或群逆的快速算法,具体如下:
(1) 根据r-特殊首尾和循环矩阵A得出f(x)和g(x);
(2) 求出f(x)和g(x)的最大公因式d(x);
(3) 若d(x)=1,根据行初等变换求出u(x),则A-1=u(Δ);

4 数值算例

解A=SFLSC2(1,2,0,-1),f(x)=-x3+2x+1,g(x)=x4-2x3-2,d(x)=1.
所以


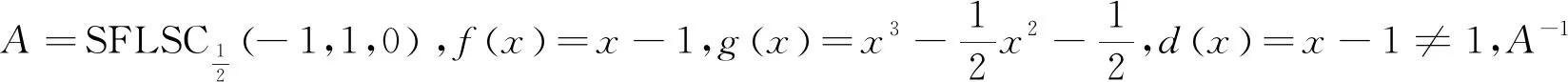
所以

5 结 论
本文通过一个基本循环矩阵,将r-特殊首尾和循环矩阵与多项式建立联系,并充分运用多项式的性质定理对矩阵的行列式及逆矩阵进行快速求解.同时,本文将r-特殊首尾和循环矩阵分为奇异和非奇异两种情况,充分讨论矩阵的逆和群逆.最后分别给出了非奇异和奇异矩阵的逆和群逆的算例,验证得出本文给出的快速算法是有效的.
