行列式解法的探讨

唐 丽

(绵阳师范学院数理学院，四川绵阳 621000)

0 引言

行列式计算是线性代数中一个重要内容，也是线性代数学习过程中一个难点.特别是高阶行列式的计算，就更是一个难上加难的事情.但就行列式的计算而言，无论是高阶还是低阶行列式，其计算的基本思想是“化零”和“降阶”，即先根据行列式的性质将行列式进行恒等变换，使之出现较多的零元素，再利用上(下)三角行列式计算或用按行(列)展开定理实现降低行列式的阶数.在研究行列式计算的相关理论的时候，许多学者就行列式的计算进行了探讨：比如文献[1-3]总结了计算行列式的常见方法与技巧：比如降阶法、三角形法、加边法，递推与数学归纳法等计算行列式.文献[4]则是探讨了三对角线变形后的行列式的算法.文献[5]探讨了一类由Fibonacci数组成的特殊行列式的计算问题.而文献[6]探讨了第三类广义Vandermonde行列式的计算结果的现实表达式.文献[7]利用母函数导出具有递推关系的行列式的计算公式.文献[8]介绍了几个行列式的基本方法与特殊方法.文献[9]则是探讨分块矩阵的行列式.但很少有学者研究行列式的翻转对行列式计算的影响.本文主要就行列式的翻转探讨了其计算.

1 行列式的翻转

根据行列式的特点，某些情况下进行行列式翻转有利于解题.而翻转，通常分为左右翻转、上下翻转，主对角线翻转和关于副对角线翻转等.每一种翻转都会有所不同，但只要掌握它们的规律，相信对于行列式计算会带来“柳暗花明又一村”的惊喜.

1.1 上下(左右)翻转

定理1设n阶行列式D=det(aij)，若D上下翻转和左右翻转后的行列式分别记为Duf和Dlf，即

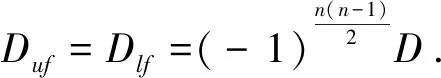
证明：第1步：把Duf中的第n行依次与第n-1行，第n-2行进行对换，…，直到第1行，共作了n-1次的相邻行对换，得行列式D1，由行列式性质得

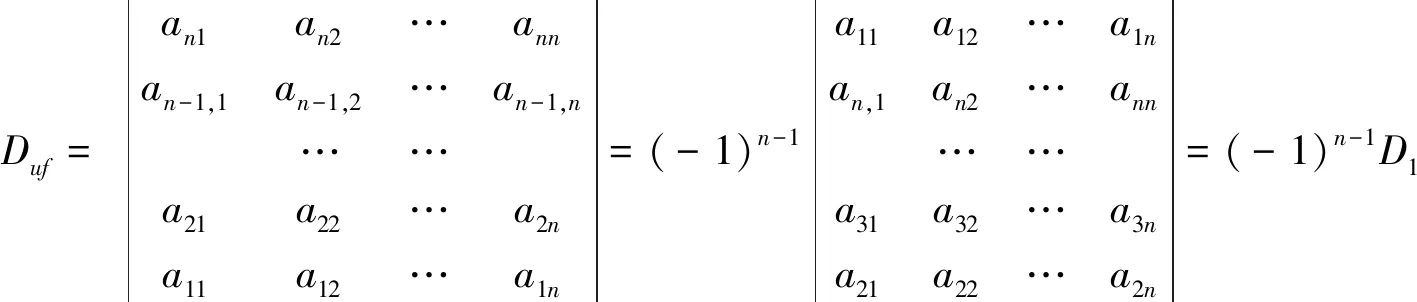
第2步：把D1中的第n行依次与第n-1行，第n-2行进行对换，…，直到第2行，即作了n-2次的相邻两行对换，得行列式D2，有

第3步：把D2中的第n行依次与第n-1,n-2行进行对换，…，直到第3行，共进行了n-3次的相邻两行对换，得到行列式记作D3，且Duf=(-1)n-1(-1)n-2(-1)n-3D3

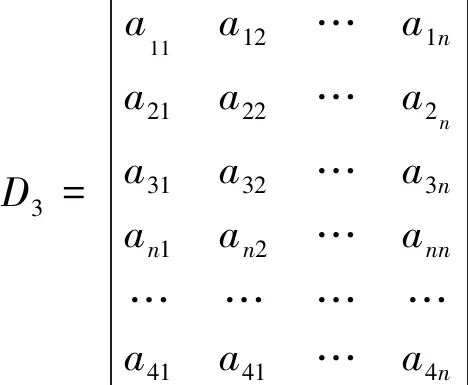
依次类推，第i步则把第i-1步的行列式Di-1的第n行依次对换到第i行，得行列式为Di，…，直到行列式Dn-2的第n行与第n-1行对换1次，得行列式Dn-1，且Dn-1=D，有

Duf=(-1)n-1(-1)n-2(-1)n-3…(-1)2(-1)1Dn-1=(-1)n-1(-1)n-2(-1)n-3…(-1)2(-1)1D

因此，从Duf到D一共进行了

所以有

第1步：把n阶行列Dif式第n列依次对换到第1列，得到的行列式记作D1′，其中

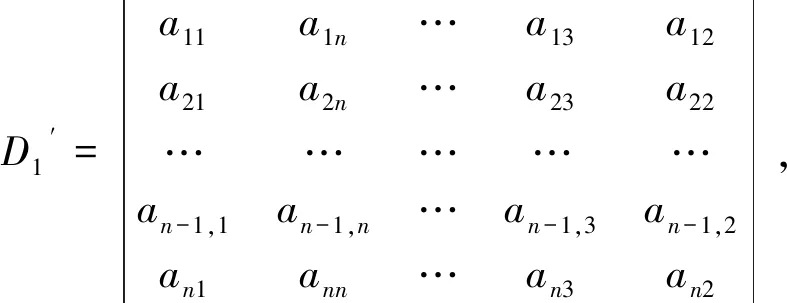
第2步：把D1′中的第n列依次对换到第2列，即作了n-2次相邻列对换,得行列式D2′，Dlf=(-1)n-1(-1)n-2D2′；

第3步：把D2′中的第n列依次对换到第3列，共进行了n-3次对换，得行列式记作Dlf=(-1)n-1(-1)n-2(-1)n-3D3′；依次类推地进行下去，…，直到行列式Dn-2′第n列与第n-1列对换1次，得行列式Dn-1′，且Dn-1′=D.因此，从Dlf到D一共进行了

所以有

因此有

证毕

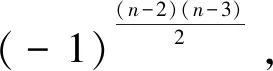
例1 计算行列式[10]

解：文献[10]提示说利用范德蒙行列式的结果.但前提是要把这个行列式表示成范德蒙行列式的形式.因此，若在这之前知道上下(左右)翻转的这样一个结果，那么就可以直接对Dn+1进行上下翻转，

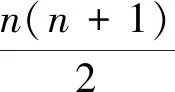
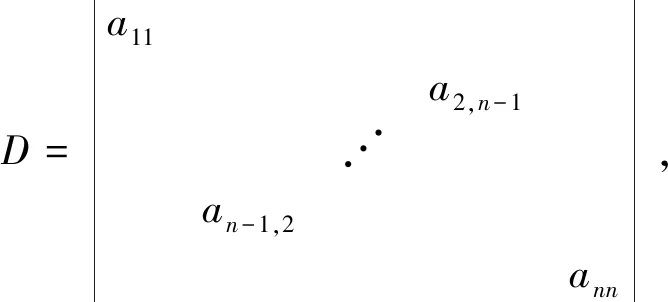
解法1：初看这个行列式，感觉是一道比较难的行列式计算题，尽管行列式中零比较多.但仔细观察，可以对行列式进行除第一列和第n列外的部分进行左右翻转.因此利用注解1，也就是对n-2阶行列式进行翻转，就可以得到一个对角行列式.

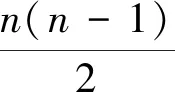
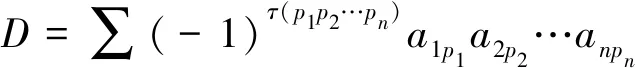
根据行列式的特点，当p1=1,p2=n-1,p3=n-2,…,pn-1=2,pn=n，D中不为零的项只有一项(-1)τ(1(n-1)(n-2)…32n)a11a2,n-1,a3,n-2…an-1,2ann，其中行标12…n为标准排列，τ(1(n-1)(n-2)…32n)为排列1(n-1)(n-2)…32n的逆序数

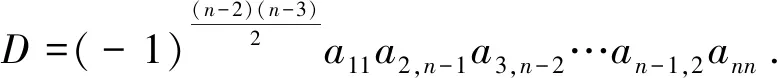
综上，通过翻转法和定义法计算例2对比发现，某些时候在计算行列式时采取翻转法会给行列式计算带来意想不到的效果.当然，除了上下(左右)翻转外，还有下面即将介绍的关于主对(次)角线翻转的问题.

1.2 主对角线和次对角线翻转

定理2 设n阶行列式D=det(aij)，D关于主对角线和次对角线翻转后的行列式分别为

则Dmd=Dbd=D.

证明：首先证明Dmd=D.D关于主对角线进行翻转，也就是把D中的第1行变成第1列，第2行变成第2列，依次类推的进行下去，最后是第n行变成了第n列，最后得到Dmd.显然，Dmd就是DT.根据行列式性质，行列式与它的转置行列式相等，所以Dmd=DT=D.

下面证明Dbd=D.

已知关于次对角线翻转得到的行列式为Dbd.那么，下面从Dbd出发，来探讨它与D的关系.Dbd经过左右翻转，再经过上下翻转，则

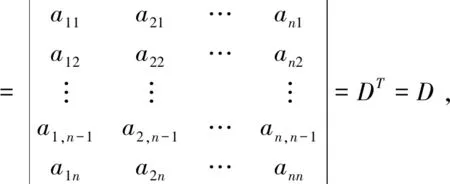
所以有Dbd=D因此，有Dmd=Dbd=D证毕

注意：在定理2中，行列式关于主对角线旋转，实际上得到的是就是行列式的转置.

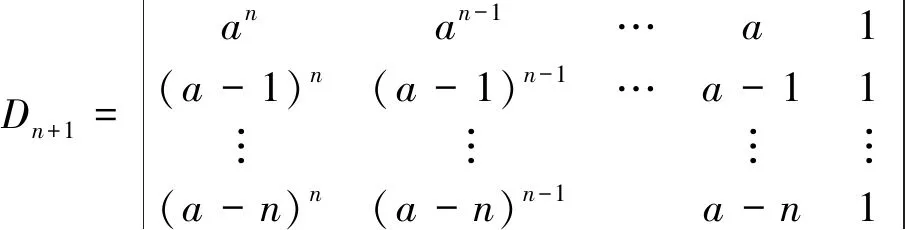
解法1：对D进行关于次对角线翻转和关于左右翻转而得到范德蒙行列式

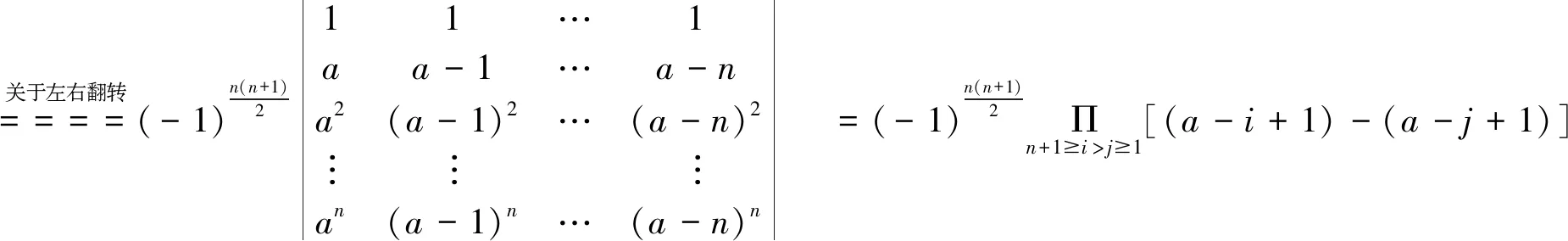
注意:为了和例1进行对比，这道题在关于次对角线翻转之后进行了左右翻转.实际上，这道题只需经过关于次对角线翻转就可以直接利用范德蒙行列式公式进行计算.例3可以如下面来解答：

解法2：由定理2知

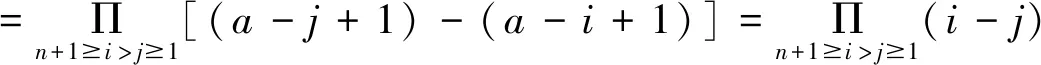
解法3：

后续解法见本题解法1.

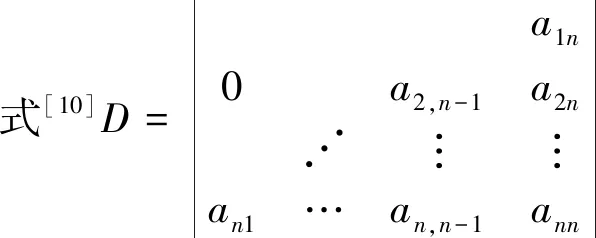
解：书上的方法这里不讲了.下面采取翻转的方法来解这道题.这是一道下三角形行列式，可以采取左右翻转，有

总结：对比书上的解法，很容易地通过翻转方法求得行列式的计算结果.事实上，即使在一般的行列式，有时候利用行列式翻转，也会让计算变得简单明了.比如下面例5.

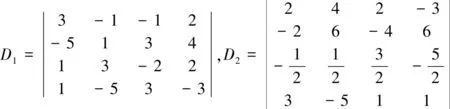
解：看到这道题时，第一直觉是应该分别把D1,D2计算出来，这样D1,D2的关系也就自然出来了，但D1,D2的计算也是挺费时的.因此想问：能不能在不计算行列式的前提下，就能把这两个行列式的关系判断出来呢？通过观察可以看出，D2的第二行与第三行都有公因子，根据行列式的性质，可以先把D2中的公因子提到行列式的外面，有

这样处理后的行列式D因为没有分数计算起来要简单些，但这里实际不用直接算出行列式.注意观察：D中的元素和D1中元素都是由±1,±2,±3,4,-5所构成的.因此考虑翻转，根据定理1和定理2，有

这样，有D1=D=D2.答案选A.

这道题所涉及到4阶行列式，若用行列式定义计算也是可以的，只是有些麻烦的；当然也可以直接把行列式化成上三角或下三角行列式进行计算.只是，若巧妙地采取行列式性质和翻转的相关定理，会让这道题变得简单且有趣，计算量也会非常的小，给人一种“柳岸花明又一村”“远近高低各不同”的美感.

2 结论

本文研究了行列式的四种翻转——上下翻转，左右翻转，主对角线翻转和关于副对角线翻转，最终以定理的形式呈现出翻转的结果.通过例题，本文总结了翻转对于行列式的计算所带来的不同效果.