一个混合核的Hilbert型不等式及其应用
2021-01-12有名辉
有名辉,宋 维
(浙江机电职业技术学院 数学教研室,浙江 杭州 310053)
0 引 言
100多年前,德国著名数学家Hilbert提出了Hilbert不等式[1]:若f,g≥0,f,g∈L2(+),则有:
(1)
其中π为满足式(1)的最佳常数因子.100多年来,数学家们通过对核函数不断地变形改造、引进参数,并通过构造新的核函数,考虑其离散型、半离散型、系数加强及高维推广,已使Hilbert不等式发展成为一个庞大的理论体系,产生了大量的新文献[2-10].其中很多研究成果与指数函数有关.2012年,杨必成[11]得到了如下齐次核的不等式:当α>0,γ>-1时,
(2)

2013年,文献[12]~[13]给出了如下含双曲正割核函数及双曲余割核函数的非齐次Hilbert型不等式:
(3)
(4)
其中,sech(t)=2(et+e-t)-1,csch(t)=2(et-e-t)-1,c0=0.915 9……为Catalan常数,μ(x)=x-3.
2019年,文献[14]构建了一个由多个双曲函数组合的核函数,并建立了相应的Hilbert型不等式,拓广了式(3)和式(4)的结果.本文构造一个与指数函数关联的核函数:
k(x,y):=e-αxyarctane-βxy,
建立一个含最佳常数因子的Hilbert型不等式,并赋予参数特殊的值,得到一些有趣的特例.为行文方便,约定p>1,1/p+1/q=1.
1 引 理
引理1 设α≥0,β≥0,α+β>0,γ>-1,k(t):=e-αtarctane-βt,
(5)
则

(6)
证明把arctane-βt展开为e-βt的麦克劳林级数,可得:
(7)
令
u=[(2k+1)β+α]t,
则有:
(8)
结合式(7)和式(8),即可得式(6).
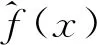
其中,n为充分大的自然数.则当n→+时,有:
(9)
证明作替换xy=t,并由Fubini定理,可知:

(10)
结合式(6)及Lebesuge控制收敛定理,可得式(9).
2 主要结果
定理1 设α≥0,β≥0,α+β>0,γ>-1,定义k(x,y):=e-αxyarctane-βxy.μ(x)=x-(pγ+1),ν(x)=x-(qγ+1),f(x),g(x)≥0,且满足f∈Lp,μ(+),g∈Lq,ν(+),则
(11)
其中,C(α,β,γ)由引理1定义,C(α,β,γ)Γ(γ+1)为满足式(11)的最佳常数因子.
证明由Hölder不等式,可知:
(12)
其中,
令xy=t,由引理1可得:

(13)
同理
(14)
把式(13)和式(14)代入式(12),得:
(15)
若式(15)可取等号,那么有不全等于零的实数A与B,使得

即
Ax-pγfp(x)=By-qγgq(y) a.e.于(0,)×(0,).
因而有常数C,使得
Ax-pγfp(x)=Ca.e.于(0,);
By-qγgq(y)=Ca.e.于(0,).
不失一般性,假定A≠0,则有:

这显然与f∈Lp,μ(+)矛盾.因而式(15)不能取等.
最后证明C(α,β,γ)Γ(γ+1)是满足式(11)的最佳常数因子.利用反证法,假如这一常数因子不为最佳,则必有0 (16) 令ε→0+,则有C(α,β,γ)Γ(γ+1)≤k,这显然与假设矛盾.因此式(11)的常数因子最佳. 定理1证毕. 在定理1中,若令α=0,则有以下推论: 推论1 设β>0,γ>-1,μ(x)=x-(pγ+1),ν(x)=x-(qγ+1),f(x),g(x)≥0,且满足f∈Lp,μ(+),g∈Lq,ν(+),则 (17) 推论2 设α>0,γ>-1,μ(x)=x-(pγ+1),ν(x)=x-(qγ+1),f(x),g(x)≥0,且满足f∈Lp,μ(+),g∈Lq,ν(+),则 (18) 从而有: 推论3 设α>0,μ(x)=x-1,ν(x)=x-1,f(x),g(x)≥0,且满足f∈Lp,μ(+),g∈Lq,ν(+),则 (19) 最后,在定理1中,令α=2β≠0,γ=0,此时 故有: 推论4 设β>0,μ(x)=x-1,ν(x)=x-1,f(x),g(x)≥0,且满足f∈Lp,μ(+),g∈Lq,ν(+),则 本文在已有文献的基础上,构造了一个新的核函数,并借助麦克劳林展开等分析的技巧,建立了一个新的Hilbert型不等式.通过引入Catalan常数等特殊常数,得到了一些新的特殊形式的Hilbert型不等式.这些新建立的结果是以往文献的拓展和补充,具有一定的理论意义和价值.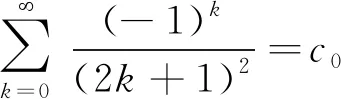


3 结 语
