基于Matlab的专业型学位研究生现代控制理论课程改革与实践

王燕锋，李祖欣，杜树新

(湖州师范学院 工学院，浙江 湖州 313000)

在国内现有的教育体制中，硕士研究生学位分为专业型和学术型.学术型研究生主要以理论研究为主；专业型研究生主要以综合应用知识的能力为目标，旨在培养适应实际工程岗位的应用型高层次人才[1-2].现代控制理论是自动化类专业型硕士研究生重要的专业基础课，是学习最优控制理论、鲁棒控制理论、非线性系统理论等其他专业课程的基础，在专业教学中具有十分重要的地位[3-4].现代控制理论是用以高等数学、常微分方程及矩阵分析为基础的状态空间分析方法，对系统的行为进行分析，涉及系统状态空间模型的建立、系统分析和控制器设计等理论，其特点是概念抽象、理论性强，对学生的数学功底要求较高，这使得很多学生在学习过程中感到课程内容晦涩难懂，不易理解和掌握.如何对现代控制理论课程教学内容进行改革，使专业型硕士研究生能够将理论与实践很好地结合起来，为后续专业课程学习打下坚实的基础，是一项急迫的课题.Matlab是由Mathworks公司开发的计算软件，主要用于数据分析、算法开发和数值计算等.本文结合Matlab相关内容，对现代控制理论课程内容改革及课程拓展进行讨论.

1 教学内容改革

设计教学内容时，教师应充分考虑学生的专业背景，将晦涩难懂的课程内容通过实际应用案例展现给学生，这样不仅能体现课程的实用性和重要性，还能激发学生的学习兴趣.同时可将Matlab软件引入课程教学，加强学生的感性认识，使课程知识与工程案例更加有机地结合起来.针对现代控制理论课程建立起与之相适应的多维立体化教学体系，这对提高教学效果有着积极的实际意义.

1.1 系统建模

建立控制系统的数学模型是对控制系统进行分析和设计的基础，也是现代控制理论课程的重要组成部分.现代控制理论用状态变量来刻画控制系统的内部特征，用微分方程组来描述系统的动态特性.状态空间模型能够描述系统输入、输出与内部状态之间的关系，揭示系统内部状态的运动特点.线性时不变系统的状态空间模型具有如下形式：

(1)

其中：x(t)∈Rn为系统的状态向量；u(t)∈Rp为系统的控制输入向量；y(t)∈Rq为系统的输出向量；A、B、C、D为适当维数的定常矩阵.

为引入和帮助学生建立状态空间方法的概念，本文选取RLC电路、阻尼系统等典型控制系统进行系统建模的介绍.

对如图1所示的RLC电路，由基尔霍夫电压定律和基尔霍夫电流定律可得：

(2)

(3)

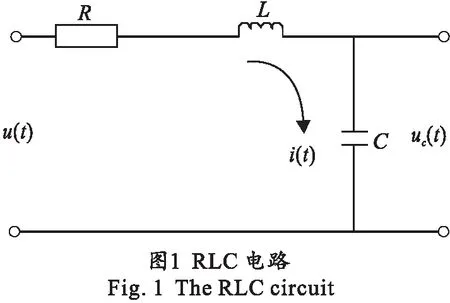
由此导入和详细介绍系统状态、状态方程、输出方程和状态空间的概念.讲授完基本的理论和概念后，再介绍Matlab相关的内容，如状态空间表达式函数G=(A,B,C,D)；传递函数命令G=tf(num,den)；模型转换命令G=tf(num,den)，G1=ss(G)；线性定常系统状态求解命令vsolve1(A,B,ut)；连续系统离散化命令sysd=c2d(sys,Ts)等.将理论问题转换为Matlab的求解问题，逐步培养学生用Matlab求解问题的能力.

1.2 控制系统的能控性与能观性

对系统(1)和指定初始时刻t0，如果存在一个时刻t1>t0，以及一个无约束容许控制输入u(t)，使得系统状态由x(t0)转移到0，那么称该非零状态x(t0)为能控的，若所有状态均为能控的，那么系统(1)为可控的.如果在有限时间区间[t0,t1]内，通过观测y(t)能够唯一确定系统的初始状态x(t0)，那么称系统状态在t0为能观的，若对任意的初始状态为能观的，那么系统(1)为可观的.在教学过程中，对能控性的讲授主要从概念入手，很难给学生一个直观的、形象的展示.事实上让学生更加容易理解和接受的定义为：在有限时间内，控制输入能否让系统从初始状态转变为要求的状态，就为系统的能控性问题；在有限时间内能否通过系统输出的测量来估计系统的初始状态，就为系统的能观性问题.

利用Matlab的ctrb(A,B)和obsv(A,C)函数，可以得到系统的能控性和能观性矩阵，进而判断系统的能控性和能观性.

1.3 稳定性判据

稳定性的定义及稳定性判据是现代控制理论的一个重点，也是难点.稳定性判据主要分为李雅普诺夫第一方法和李雅普诺夫第二方法.李雅普诺夫第一方法为：对于线性定常系统，平衡状态xe=0渐近稳定的充要条件是系统矩阵A的所有特征值均具有负实部.李雅普诺夫第二方法又称作直接法，它的基本思路不是通过求解系统的运动方程，而是借助李雅普诺夫函数，以及根据系统状态方程所计算得到的李雅普诺夫函数导数或差分来直接判断系统的稳定性.李雅普诺夫第二方法不但是系统稳定性分析的重要方法，而且是控制系统控制器设计的主流方法.在讲授这部分内容时，教师可以将基于线性矩阵不等式(linear matrix inequality, LMI)系统镇定方法与Matlab LMI工具箱的使用方法结合起来介绍.通过实例将李雅普诺夫第二方法、LMI技术和系统镇定等知识点进行综合.

考虑如下离散控制系统：

x(k+1)=Ax(k)+Bu(k),

(4)

设计状态反馈控制器使得闭环系统渐近稳定.

设计状态反馈控制器使闭环系统稳定的方法有多种，如教材里介绍的极点配置方法.为更好地培养学生的科研能力，教师可以结合LMI技术讲授控制器设计的方法.将状态反馈控制律u(k)=Kx(k)代入系统(4)，可得闭环系统为：

x(k+1)=(A+BK)x(k).

(5)

构造如下的李雅普诺夫函数：

V(k)=xT(k)Px(k),

(6)

其中，P为正定矩阵.

由式(5)和式(6)得：

ΔV(k)=xT(k)[(A+BK)TP(A+BK)-P]x(k).

(7)

由李雅普诺夫稳定性理论可知，若

(A+BK)TP(A+BK)-P<0

(8)

成立，那么闭环系统(5)是渐近稳定的.

由Schur补引理可得，式(8)等价于：

(9)

进一步式(9)等价于

(10)

令P-1=S及KP-1=Y可得：

(11)

那么控制器增益矩阵K=YS-1.显然式(11)是严格的LMI，可以使用Matlab LMI 工具箱进行求解.

1.4 状态观测器设计

实际工程中能测量的信号是系统的输出，而不一定是系统的状态，且系统的状态不一定是物理量，因此不是所有的状态变量都可以测量得到的.当系统的状态不能全部得到时，就无法利用状态进行反馈控制.状态观测器解决了系统状态不可测的问题.状态观测器的基本原理是利用容易测量的系统控制输入和输出,从而对系统的状态进行估计.

状态观测的状态方程具有如下形式：

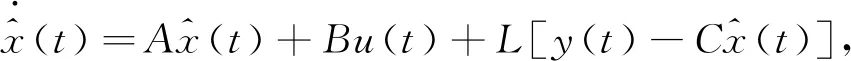
(12)

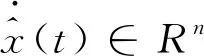
为对系统状态进行有效估计，要求

(13)

定义状态估计误差:

由式(12)和式(1)可得：

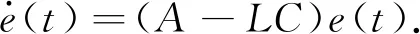
(14)

矩阵A-LC的极点决定状态估计误差e(t)的衰减速度.为使状态估计误差衰减到零，需要选择合适的矩阵L，使矩阵A-LC的特征值全部在左复平面.

应用Matlab命令可以直接得到观测器的增益矩阵：

L=[place(A′,C′,V)]′，

其中，V为A-LC极点所组成的向量.

考虑如图2的角度位置跟踪系统，图中φr为天线的角度位置；φ为移动物体的角度位置.该系统的作用是通过对电机施加电压u，使天线随着目标物体的移动而旋转，并满足φ≅φr.

角度位置跟踪系统的状态空间方程为:

(15)

使用(Matlab place)命令，可得状态观测器矩阵为：

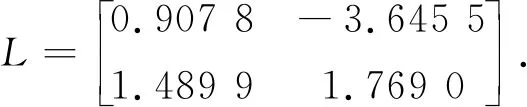
2 知识拓展

教学中教师可将相关科研成果[5-8]反馈于教学，这不仅对学生深入理解和掌握相关知识点具有积极的作用，还对引导学生进行科研，提高学生的科研水平具有实际意义.如将具有传感器至控制器时延,以及控制器至执行器时延的网络控制系统的建模、控制器设计等内容讲授给学生，培养学生利用已学知识进行科研的能力.

具有双侧时延的NCS结构如图4所示，其中τ(k)表示S-C时延；d(k)表示C-A时延.

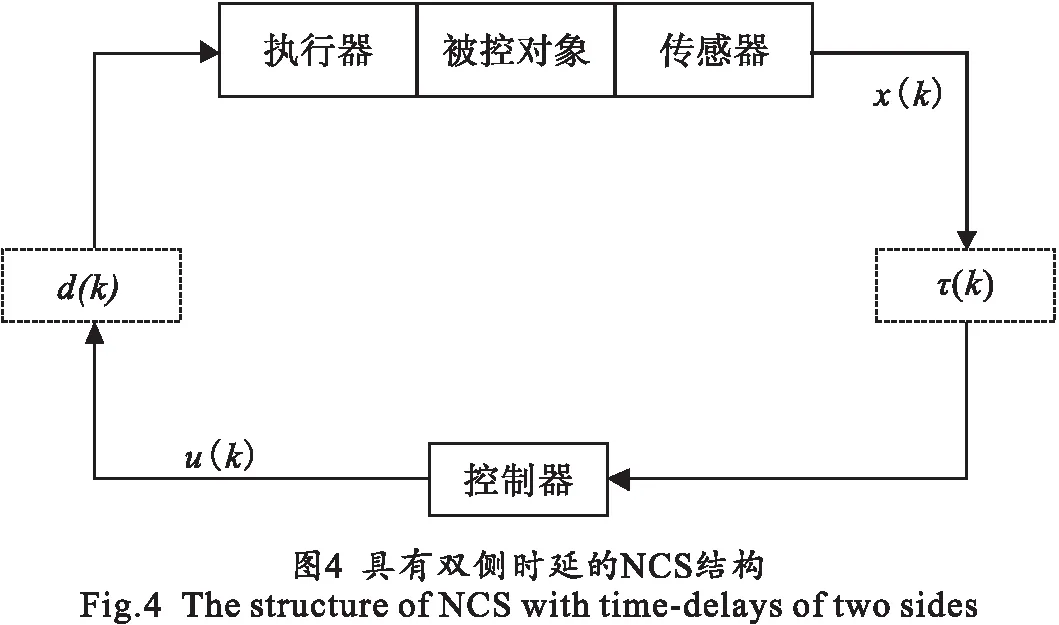
τ(k)及d(k)为有限状态的Markov链，分别从M={0，1，…，τ}及N={0，1，…，d}取值，其转移概率矩阵分别为Λ=[λij]及Π=[πrs]，即：

λij=Prob{τ(k+1)=j|τ(k)=i},πrs=Prob{d(k+1)=s|d(k)=r}.

(16)

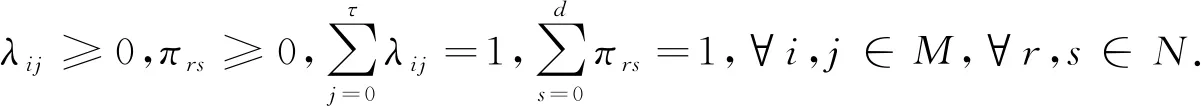
考虑如下时不变线性被控对象：

x(k+1)=Apx(k)+Bpu(k),

(17)

其中：x(k)∈Rn为系统状态向量；u(k)∈Rm为控制输入向量；Ap∈Rn×n及Bp∈Rn×m为定常矩阵.

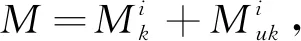
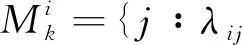
(18)

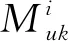
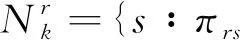
(19)

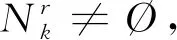
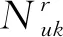
采用如下状态反馈控制律：

u(k)=Kx[k-τ(k)-d(k)]，x(k)=η(k)，k∈{-τ-d，…，0}，

(20)

由式(17)和式(20)可得闭环系统表达式：

x(k+1)=Apx(k)+BpKx[k-τ(k)-d(k)]，x(k)=η(k)，k∈{-τ-d，…，0}.

(21)

定义增广向量:

闭环系统(21)可以写为：

(22)

其中:

定理1 如果存在正定矩阵Pi，r>0，Fi，r>0,及矩阵K使得如下不等式:

(23)

(24)

(25)

(26)

Fj,sPj,s=I，j∈M,s∈N,

(27)

其中:

对于所有的i,j∈M,r,s∈N成立，那么使闭环系统(21)随机稳定的镇定控制器(20)存在.

假设S-C时延τ(k)及C-A时延d(k)分别从M={0,1}及N={0,1}中取值，其转移概率矩阵分别为：

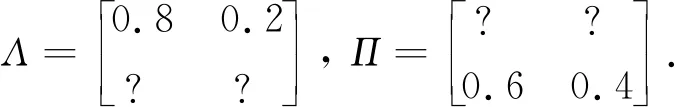
根据定理1，得到控制器增益矩阵为：

K=[-1.112 6 -0.738 0].

假设系统初始状态为：

x(-2)=x(-1)=[0 0]T,x(0)=[-1 1]T,

闭环系统状态曲线如图6所示.

3 结 论

由于教学案例的引入，学生建立了理论知识与实际工程问题之间的联系，改变了对现代控制理论课程完全是用来解决数学问题的错误认识，从而能够从实际工程系统的角度来把握课程内容.从学生的反馈来看，通过课程改革提高了大部分学生学习兴趣，教学效果显著提高，如部分研究生已参与发表了多篇高水平科研论文，也有些研究生成功申请到了省教育厅科研项目(研究生培养专项).通过对该课程的学习，学生增强了科研能力及工程应用能力，为后续课程的学习及从事相关工程工作岗位奠定了良好的基础.在未来教学中我们会更加注重将抽象理论转化为学生易理解、易接受的教学手段的研究，结合现代化仿真模拟技术将更多的典型案例引入到教学中.