工作记忆负荷水平对学生口算能力的影响

何男 赵继源 朱惠英 王文义

【摘 要】本文分析义务教育阶段三至九年级学生在不同记忆负荷水平的口算题目中的表现，发现学生口算能力与工作记忆负荷水平、工作记忆系统各成分、所在年级、策略与经验等都具有一定联系，提出训练学生选择不同策略进行计算以减轻记忆负担，加强基础运算的练习与记忆，抓住干扰因素，把握教学难点，突破记忆难题与运算困境等做法。

【关键词】口算能力 工作记忆 工作记忆负荷水平

【中图分类号】G 【文献标识码】A

【文章编号】0450-9889（2021）30-0128-04

数学在生活中有着举足轻重的作用，而数学运算能力作为数学关键能力之一，在数学教育中也受到高度重视。口算作为一种独立的运算形式，是学生解决其他数学问题的辅助力量;口算水平的高低是运算能力和数学综合能力的重要体现。在以往的研究中，内容上偏向于研究影响口算能力的因素，主要有题目进退位、策略选择与心态等;对象上侧重于低学段儿童，忽略了初中生，更缺少对小学到初中口算发展变化的研究;测试选题上偏向于加法，较少涉及多项式和方程。然而，口算从心理机制来看，与工作记忆中的存储和加工相关，因此口算与记忆（特别是工作记忆）的研究值得进一步展开。

当我们把影响因素缩小到工作记忆负荷、研究范围扩大到义务教育阶段时，应重点关注以下几个问题：工作记忆负荷如何影响学生的口算能力？学生口算不同工作记忆负荷的题目时表现出怎样的特点？题目负荷及工作记忆水平对口算能力的影响在不同年级有何异同？通过对这些问题的探讨，我们希望进一步了解工作记忆负荷水平与学生口算能力的关系，为广大师生提出建议，让运算能力的发展成为学生数学素养提升的关键力量。

一、实验及其方法

（一）相关概念

1.口算与口算能力

本实验的口算是指被试在听到主试口述题目（不允许被试看到考题）后，不借助任何演算工具，仅凭借自身记忆题目及在心中计算题目，直接说出最终答案。此次研究在量化的基础上进行，选用口算正确率作为口算能力的衡量指标。

2.题目的工作记忆负荷

Wanner与Shiner提出“加法口算广度”一词来衡量加法口算能力，其计算方式为加数与被加数的位数之和。但此衡量方法不利于解释因是否进位而带来的不同“负担”。并且，本实验测试内容包含四则运算与方程，需要一个更具普遍意义的衡量指标或测验标准。

工作记忆是一种暂时存储与加工信息的有限记忆系统，个体能承担的最大工作记忆负荷数与工作记忆水平及活动表现直接相关。本实验引入M、N两个变量：M表示个体一次活动能同时记忆并暂时存储的项目总数，如2、5x可看作一个项目数，个体因工作记忆水平的差异所记忆的一个项目大小会有所不同;N指对已进入记忆的项目在头脑中进行运算操作的累计加工次数，如3+4=7，对记忆过的3和4共进行一次加工，N为1。本实验用M+N衡量工作记忆负荷的大小，此设定符合工作记忆系统的特点，兼顾了记忆与加工两个方面。

3.工作记忆水平与M+N的关系

M+N的数值越大，表明题目承载的工作记忆负荷越大，对学生的工作记忆水平要求越高。当被试完成M+N数值较大的题目时，可认为被试在口算时的工作记忆水平较高。若M+N数值较大的题目正确率较低，可以猜测工作记忆水平较低的学生在完成口算测试时的表现较差。通过引入M+N，以定量的方法将工作记忆负荷、工作记忆水平与口算能力联系起来。

（二）被试

本研究选取南宁市某乡镇学校三至九年级部分学生进行口算测验，各年级选取按数学成绩分为好、中、差的被试各两名。

（三）实验材料

因没有找到现成的有普遍意义的试卷，主试依据数学课标与教材编制题目。以预测试检验试题信度与效度，结合在职教师的意见进行修改完成，得到各年级口算试卷和访谈表各1份。试卷特点：（1）每份试卷的题目数量为21至28题，不规定完成时间，但原则上不超过20分钟;（2）为贴合学生身心发展特点，每份试卷大体上按内容的难易、记忆负荷的大小、运算的复杂程度等进行编排;（3）为纵向研究小学到初中各年级口算能力在工作记忆影响方面的变化趋势，三至九年级保留一定公共题目。

（四）实验程序

1.口算测试

口算测试由主试、被试双方在安静的环境下单独进行，被试在听到主试口述题目后，不借助任何工具直接说出答案。若被试没有听清，主试可重复一遍;若被试不会该题，可跳过此题，直至全部题目回答完毕。对测试全过程进行筆录与录音。

2.口算访谈

每个被试完成口算测试后，紧接着对其进行访谈，对访谈全程进行笔录与录音。

3.数据收集与整理

（1）舍弃无效数据。（2）为贴合研究目的，避免学生因不会而答错，题目设置得较简单。被试有一次答错的机会，若第二次答对则记为正确，若第二次仍错则记为错误。（3）将各被试的每题结果、每名被试的正确率、每道题的正确率汇总在Excel表内。（4）对录音及访谈中展现的问题进行归类。

二、实验结果

口算需要被试将题目记忆后再加工，故M总是≥2的，即不存在M=0或1，N=k（k≥1）的情况。当数字较大或运算复杂时，被试需记忆的项目数较多，M+N的值也会有多种情况。本实验结果统计显示，M+N最小为2，最大为7。为使实验结果更加简洁明了，将M+N的数值进行水平划分，最终化为以下三个水平。

低负荷水平：M+N=2（M=2，N=0），M+N=3（M≥2，0≤N≤1）。中负荷水平：M+N=4（M≥2，0≤N≤2）、M+N=5（M≥2，0≤N≤3）。高负荷水平：M+N=6（M≥2，0≤N≤4）、M+N=7（M≥2，0≤N≤5）。

（一）M+N的水平与一个年级口算情况的横向分析

下面以三年级为例，其他年级统计与分析方式相同。

低负荷水平题目：5+4，15-5，12÷4，3×5，45÷9，16-7，13×3，300+15，4200-200。中负荷水平题目：34+12，27+16，54-32，430+80，630-40，123×3，35-17，26×17，123×4，301×5。高负荷水平题目：133×5，145+66，125-38。

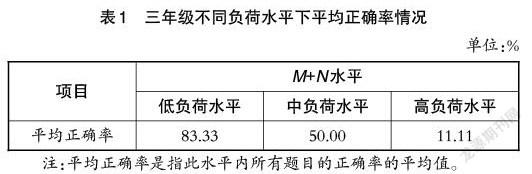
由表1可知：用平均正确率反映某一工作记忆负荷水平下的口算结果，随着M+N值的增大，平均正确率降低，即工作记忆负荷水平与口算成绩呈负相关。

结合访谈得出：（1）N值影响加工复杂度从而干扰运算过程。易错题通常位数较多且有进退位，学生解释“忘记前一步结果、忘记进位”等，这表明N值的增大使学生在运算过程中易出现纰漏。（2）M值关联记忆容量从而干扰结果整理。项目数较多的题目难以读取且计算中易被反复遗忘，这表明M值的增大对学生形成结果有困难。

由表2可知：工作记忆负荷最小的题目与负荷最大的题目的正确率相差很大，这再次印证了记忆负荷会影响口算结果。

结合访谈得出：（1）在记忆项目数上，5+4只需记忆两个数字，而对于133×5，即便记忆水平较好的学生能将133记为一个项目，也仍需记忆多位数乘一位数的中间结果与进位等多个项目，即M值影响了正确率;（2）在加工次数上，5+4=9多来自长时记忆，不需任何操作，N此时为0，但绝大部分学生解答133×5都需在头脑中“列竖式”，又含3×5，3×5+1，1×5+1等多次加工，即N值影响了正确率。

由表3可知：（1）好、中、差学生的正确率均随负荷水平的上升而降低，错误多集中于高负荷水平题目，表明负荷水平对不同程度学生的影响是一致的，个体间从中负荷水平的题目开始拉开差距。（2）数学成绩与口算水平呈一定正相关，但不绝对。好2与中2的口算成绩相同，经访谈得知，中2的记忆力与计算能力较好，好1平时依赖于笔算，表明口算对记忆与思维加工要求较高。（3）工作记忆容量是影响工作记忆水平和口算成绩的重要因素。差2的正确率最低，在计算13×3时，得到十位之后，忘记了个位是9，其他题目错误原因类似，其源头是工作记忆容量小。（4）学生表示“若是笔算就不会出错”，说明位数、中间结果以及进退位的增多都会通过加重学生的记忆负担来提高错误率。

（二）M+N的水平与多个年级口算情况的纵向分析

由表4可知：（1）各年级正确率基本上随题目负荷水平的上升呈下降趋势，表明记忆负荷水平对口算成绩有较大影响且这种影响在不同年级具有一致性。（2）随着年级的上升，任一负荷水平题目的正确率基本呈上升趋势。结合访谈得知，学生对题目的熟练程度及知识体系的丰富性可以克服工作记忆负荷带来的困难。（3）负荷水平导致的口算成绩差距在低年级中更加突出。八、九年级的整体差距与三、四、五年级相比较小，结合访谈得知，年龄小的被试在答题时对记忆及思维加工依赖较大。

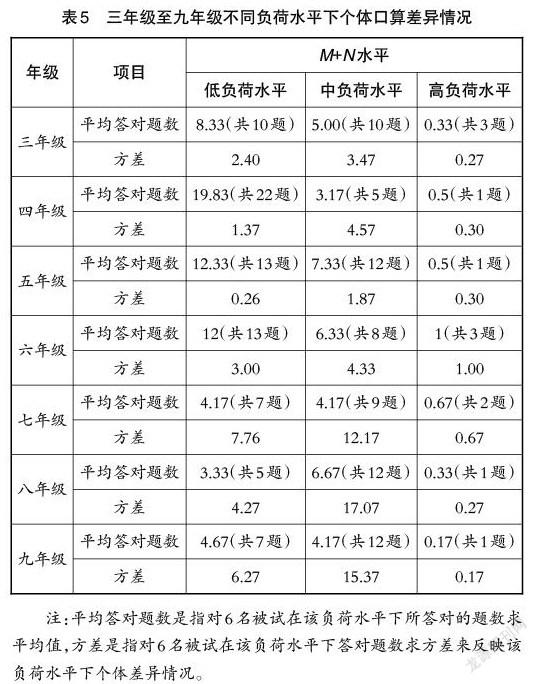
由表5可知：（1）各年级的三个平均答对题数具有相同规律，即低负荷水平的答对题数占该负荷水平题数的比例大于50%，中负荷水平的答对题数占比在50%左右，高负荷水平的答对题数占比不超过50%;（2）各年级的三个方差具有相同规律，即中负荷水平的方差最大，低负荷水平与高负荷水平的方差较小。这表明当题目负荷水平适中时，6位被试的口算成绩差异较大;当题目负荷过小或过大时，被试之间的个体差异不显著。

结合访谈得出：低负荷水平的题目对所有被试的“记忆负担”都较轻，好、中、差学生基本上能完成这一水平的题目，个体差异较小;高负荷水平的题目令所有学生都感到困难，个体差异也较小;而题目负荷程度适中时，工作记忆水平较高的学生就会与其他学生拉开差距，记忆水平低的学生错误率升高，个体之间的差异开始显著。

（三）M+N的水平与相邻年级公共题目正确率的对比分析

由访谈可知：[512]×[35]是小学内容，七年级的学生部分选择先相乘后约分，使约分时记忆负荷较重;或约分两个5后没有注意3与12还能约分，即因信息过多而使视空间模板负荷较重且对位置信息缺乏足够的灵敏度。七年级的学生刚接触一次方程，2x+4=1需依靠笔算，因需同时记忆移项、同除、符号而无法兼顾。九年级的学生学习二次方程时最终都要化为一次方程来求解，因练习较多而不再容易忽视各部分内容。

由表6可知：（1）初中生口算能力随年级升高大体上有所上升，九年级较七、八年级的优势更显著，且各负荷水平的题目均满足此规律;（2）信息过多使记忆容量不能满足题目要求，而位置信息比较重要的题目会加重视空间模板的负荷;（3）学生通过加大练习、积累经验，改善记忆与加工能力，从而提升工作记忆水平;（4）策略的选择会给工作记忆带来不同负荷的任务，进而影响口算成绩。

（四）M+N的水平与口算成绩不相一致的个例分析

同一负荷水平下，有時看似运算复杂或记忆项目多的题目反而正确率较高。由表7及访谈可知：（1）口算成绩受长时记忆的影响。五年级低负荷水平题目0.25×4包含两位小数，需进位两次，1.1×2包括一位小数，不需进位，但前者的正确率高于后者，这是因学生从长时记忆中提取了25×4=100的答案。（2）口算成绩受语音环路的影响。九年级中负荷水平题目（[6]+[3]）（[6]-[3]）可通过公式简便计算，然而学生在提取信息时语音环路负荷较重，无法认识其形式的特殊，从而停滞不前。（3）语音环路负荷较重有时是“假象”，可能是情境缓冲器的干扰所致。部分学生听不懂题目是因为对一道包含[6]、[3]、加减乘法及小括号的题目产生畏惧心理，受情绪心态的影响而无法专心提取、记忆并加工信息。

三、分析讨论

（一）工作记忆负荷水平对口算能力的影响机制

经研究发现：（1）工作记忆负荷水平通过加大信息存储与加工的难度进而影响口算，即M+N的值与口算成绩呈显著相关，与Wanner和Shiner在口算能力和工作记忆的关系研究中的结论一致，即口算与短暂存储和加工两个方面相关;（2）负荷过高会影响系统各子成分进而影响口算的正确率，位数过多与进退位给语音环路和视空间模板带来干扰，信息读取困难或加工复杂加重了对情境缓冲器的扰乱，再次验证了Baddeley和Hitch提出的工作记忆的工作机制。

（二）工作记忆负荷水平对口算能力影响的个体差异和年级差异

经同一年级的横向对比及不同年级的纵向比较发现：负荷水平对不同年龄特点与发展特点的学生的影响具有一致性，但存在个体差异;随着年级的增长，不同负荷水平的题目正确率呈上升趋势，这与任毅梅得出的口算能力随年龄增长逐渐提升的结论相吻合。

（三）影响口算能力的其他因素

Beishuizen等的“心算与策略使用研究”涉及运算能力与策略的关系。本实验发现，策略选择影响后续工作记忆负担，进而影响口算难度。Ashcraft提出儿童对算术问题答案的提取是在长时记忆中进行的，这与实验中长时记忆对口算的推动具有一致性。我国学者张奇在对小学生口算能力发展研究中发现口算能力与熟练程度相关，而本实验也发现练习与经验积累有助于口算能力的提升。

四、实验结论

（1）工作记忆负荷水平与口算成绩总体上呈负相关，记忆数M及加工数N的增大使工作记忆负担加重从而正确率下降。（2）N值通过加工复杂度干扰运算过程，M值通过记忆容量干扰结果整理，暂时存储与认知加工是影响口算成绩的重要原因。（3）题目的负荷水平对不同层次学生的口算影响具有一致性。好、中、差学生的错误多集中于高负荷水平的题目，低负荷水平与高负荷水平的题目正确率差距较大，学生之间从中负荷水平的题目开始拉开差距。（4）负荷水平对口算的影响在不同年级具有一致性，因负荷水平导致的成绩差距在低年级中更加突出。当题目负荷水平适中时，个体差异较大;当题目负荷过小或过大时，个体差异不显著。（5）从工作记忆系统的成分来看，题目信息过多会通过加重语音环路负荷来影响信息提取，位置信息过多以及运算复杂会通过加重视空间负荷来影响信息加工，心态错误或情绪波动会通过情境缓冲器间接影响其他成分正常工作，表明口算能力受工作记忆各个成分的影响。（6）影响口算能力的其他因素：数学成绩与口算能力呈一定的正相关，但不绝对;策略的选择通过影响负荷水平间接影响口算成绩;练习的增加与经验的积累会通过提高工作记忆水平从而提升口算能力。

针对本研究結果提出如下教学建议：（1）注重培养学生的思维能力，训练学生选择不同策略进行计算以减轻记忆负担;（2）加强基础运算的练习与记忆，为解决复杂问题提供素材与经验;（3）抓住干扰因素，把握教学难点，突破记忆难题与运算困境，严防教学避重就轻;（4）正确引导学生的学习态度，协助学生管理情绪，为解决人生问题提供坚实基础。

【参考文献】

[1]吴晓红，谢明初.口算的本真意义及其在小学数学教学中的异化[J].数学教育学报，2005（2）.

[2]任毅梅.儿童心算能力与工作记忆发展的实验研究[D].天津：天津师范大学，2000.

[3]张奇，林崇德，赵冬梅，等.小学生口算能力的发展研究[J].心理科学，2004（3）.

【作者简介】何 男（1997— ），女，河南平顶山人，硕士研究生学历，主要研究方向为数学教育;赵继源（1963— ），男，广西天等人，博士，教授，现就职于南宁师范大学数学与统计学院，主要研究方向为数学教育心理学、教师教育、数学教学论;朱惠英（1999— ），女，广西贺州人，硕士研究生学历，主要研究方向为数学教育;王文义（1997— ），男，山东青岛人，硕士研究生学历，主要研究方向为数学教育。

（责编 唐玉萍）