反应釜夹套封口锥和凹口锥翻边结构的应力分析和优化设计

左安达

（惠生工程（中国）有限公司，上海 201210）

夹套反应釜是石油化工行业反应装置中比较常见和典型的设备，夹套与设备内筒外表面形成密闭的空间并在此空间内通入载热流体介质与本体内工艺介质进行传热，以维持本体内工艺介质的温度需求[1]。本文所述夹套结构形式为U 型整体夹套（包覆范围为下封头和部分设备筒体），U 型夹套以其结构简单方便且基本不需要维修的优势在行业中应用最为广泛[2-3]，其结构上的主要特点是：与设备内筒外表面相焊形成封口锥（图1）以满足密闭空间的要求，另有为避开内筒上工艺管口将夹套局部进行翻边形成的凹口锥（图2）；其承载上的主要特点是：具备两个压力腔，夹套部分承受夹套内压或外压载荷，被夹套包覆的内筒部分则同时承受内筒内压、夹套内压或外压载荷，载荷组合的危险工况较多，不仅需要进行内压强度检核，还需进行外压稳定性校核[4]。封口锥和凹口锥翻边结构与夹套或内筒连接位置总体结构不连续，在内压或外压作用下会产生较大的局部薄膜应力或弯曲应力，如果同时存在温差波动的情况，则还需考虑温差应力[5]的耦合影响，则受力状态更为复杂，常规计算已无法满足要求。本文基于某一反应釜设备，采用有限元分析法对封口锥和凹口锥总体结构不连续处的高应力区进行应力计算和划类，直观地对翻边结构的受力状态和应力变化规律进行探讨和理论分析，以期能够为工程实际提供一定的参考价值和设计依据[6]。

1 结构尺寸和设计性能参数

为满足封闭空间要求，U 型夹套与内筒之间需要通过封闭件连接起来，而最常用的封闭件为锥形封闭件（本文称之为封口锥），封口锥受力状态较好、相同条件下耗材少且有良好的加工工艺性，还可通过带圆弧的过渡段进一步优化受力状态。反应釜的内筒体被夹套筒体包覆，内筒上的接管需经过夹套筒体引出至工艺管线，而最常用的结构是将夹套筒体在接管周围进行翻边弯制后与内筒焊接（本文称之为凹口锥），凹口锥翻边后与内筒焊接还可对内筒起到一定的附加加强作用。反应釜封口锥和凹口锥翻边结构尺寸分别如图1、2 所示。

反应釜的相关设计参数和材料性能参数分别见表1、2。

图1 封口锥结构尺寸Fig.1 Dimension of sealed-cone structure

2 封口锥和凹口锥翻边结构有限元分析

2.1 有限元模型和网格划分

由于分析模型中几何结构、材料、载荷和边界条件均具有对称性，故采用1/2 模型施加对称边界条件既能保证计算精度又可缩短计算时间，网格采用全六面体网格保证网格质量并在应力重点关注区域细化网格，单元采用Solid 186 单元，内筒长度和夹套筒体长度均远大于边缘应力衰减长度（ .R2 5δ，如图1、图2 所示），不会影响封口锥和凹口锥总体结构不连续处应力的分布情况[7-8]。本文封口锥和凹口锥翻边结构分别各建立了六种模型，探讨了不同翻边角度下（α=15°、30°、45°、60°、75°）高应力区应力变化趋势和规律。模型和网格划分分别如图3、4所示（α=45°）。

图2 凹口锥结构尺寸Fig.2 Dimension of notched-cone structure

表1 相关设计参数Table 1 Related design parameters

表2 材料性能参数Table 2 Characteristic parameters of material

2.2 设计工况和载荷、位移边界条件的施加

本计算模型不考虑设备自重、风载荷、地震载荷及内装物料的重量（根据设计参数和工程经验，这几类载荷对本设备计算结果的影响极小），仅考虑设计压力的作用。该设备具有两个压力腔，且压力并不是始终同时存在的，因而需分别计算三种设计工况下压力对封口锥和凹口锥高应力区在不同翻边角度下应力分布的影响规律（表3），但设计工况二、设计工况三与设计工况一仅压差大小和方向不同，本质上承载后结构总体应力变化趋势相同。限于篇幅有限，本文仅列出了两腔压力同时作用时（设计工况一）封口锥与凹口锥随翻边角度改变的应力变化趋势和规律，内筒和夹套筒体分别施加相应的设计压力并赋予不同的材料属性（见表2），对于封口锥结构模型，内筒上表面施加环向和轴向位移约束，内筒和夹套下表面分别施加对应的等效压力；对于凹口锥结构模型，内筒和夹套下表面均施加环向和轴向位移约束，上表面则分别施加对应的等效压力[9]。

图3 封口锥翻边结构有限元模型和网格划分Fig.3 Finite element model and meshing of sealed-cone structure

图4 凹口锥翻边结构有限元模型和网格划分Fig.4 Finite element model and meshing of notched-cone structure

表3 设计工况Table 3 Design conditions

3 有限元分析结果讨论

3.1 封口锥翻边结构应力变化趋势

封口锥与内筒翻边连接结构存在两个总体结构不连续区域：一是锥壳大端与夹套筒体连接处过渡段区，二是锥壳小端与内筒连接区。此两区域在各自压力或压力差作用下产生薄膜应力，同时为满足变形协调产生较大的弯曲应力及附加的峰值应力，属于需重点关注的高应力区。两腔压力同时作用下封口锥翻边结构在不同翻边角度下的应力变化趋势如图5 所示。

图5 封口锥翻边结构在不同翻边角度下的应力变化趋势Fig.5 Stress distribution of sealed -cone structure under different flanged-angle

由图5 分析可知：在α=15°时，最大应力值为127.82 MPa，出现在锥壳大端与夹套筒体连接过渡段内表面。随翻边角度α的增大，在α=15° ～ 45°之间最大应力位置仍在过渡段内表面且应力值逐渐增大至302.79 MPa，同时不难看出，锥壳小端与内筒连接处应力也逐渐增大。当翻边角度增大到α=60°时，最大应力值位置发生变化，由锥壳大端与夹套筒体连接过渡段内表面转移至锥壳小端与内筒体连接处外表面，且随翻边角度继续增大到α=75°时，最大应力值由410.76 MPa 增大到529.97 MPa，应力值显著增 大。

3.2 封口锥翻边结构应力线性化后各类应力变化规 律

为进一步分析上述两个高应力区的应力变化规律，本节在结构应力较大且需重点关注的区域定义了四条路径，将线性化后的薄膜应力、弯曲应力和峰值应力进行归类并分别探讨各类应力的变化规律，以便更直观地对各类应力的变化趋势及产生的原因进行分析。线性化路径及路径下各类应力在不同翻边角度下的变化规律分别如图6、7 所示。

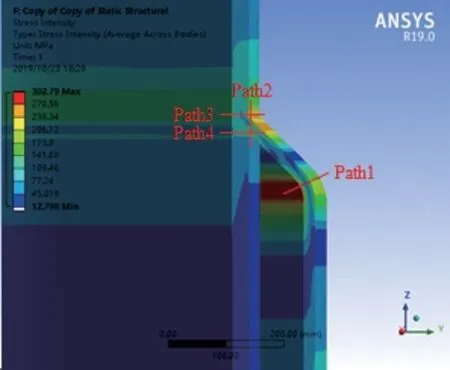
图6 高应力区域线性化路径（Path 1 ～ Path 4）Fig.6 Linearized path at high stress region

图7 线性化路径下各类应力在不同翻边角度下的变化规律Fig.7 Stress distribution under different flanged-angle at linearized path

由图7a 分析可知：对于封口锥大端与夹套筒体连接过渡段内表面（Path 1），随翻边角度α的逐渐增大，薄膜应力呈先增加后减小的趋势（α=45°时开始减小），峰值应力呈轻微增长趋势，但两者变化幅度均极小；而弯曲应力则呈显著增大的趋势（从α=15°时的60.6 MPa 到α=75°时的295.9 MPa，增幅约4 倍），进而导致总应力亦显著增大。分析认为，薄膜应力产生的原因主要由两部分组成：一是为满足静力平衡而产生的一次总体薄膜应力且起主导作用，二是因结构总体不连续产生了极小的具有二次性质的局部薄膜应力且受翻边角度影响不大，因而总的薄膜应力变化幅度很小；同样，弯曲应力产生的原因亦主要由两部分组成：一是为满足静力平衡而产生的一次弯曲应力，二是因结构总体不连续为满足变形协调而产生的二次弯曲应力，且随翻边角度的增大，锥壳趋向于平板结构，此时一次和二次弯曲应力均会显著增大进而导致总弯曲应力的显著增大；峰值应力因有过渡圆角的存在，产生的应力值很小且受翻边角度影响甚微。由图7b 分析可知：对于封口锥小端与内筒体连接处的夹套段外表面（Path 2），随α的逐渐增大，薄膜应力呈轻微增加趋势且变化幅度极小；而弯曲应力亦呈显著增大 的 趋 势（从α=15° 时 的21.9 MPa 到α=75° 时 的375.4 MPa，增幅达到约16 倍），远远大于Path 1路径上的增幅，同时峰值应力在α＞45°后增幅较大，进而导致此处最大总应力值超过锥壳大端过渡段内表面。分析认为：主要是此处为满足变形协调产生的二次弯曲应力急剧增大导致的。由图7c、d分析可知：对于与封口锥小端连接的内筒体（Path 3、Path 4），薄膜应力总体变化趋势分析同上，弯曲应力值总体较Path 2 路径小很多，且在Path 3 路径上α＞45°后弯曲应力甚至逐渐减小，峰值应力则随α的增大有显著增大趋势。分析认为：连接处筒体刚度较大，弯曲变形主要由刚度较小的夹套来承担，故Path 2 的弯曲应力值远大于Path 3 和Path 4，而Path 3 弯曲应力的减小是因部分弯曲应力方向相反抵减所致。

3.3 凹口锥翻边结构应力变化趋势

凹口锥与内筒翻边连接结构同样存在两个总体结构不连续区域。两腔压力同时作用下凹口锥翻边结构在不同翻边角度下的应力变化趋势如图8 所示。

由图8 分析可知：在α=15°时，最大应力值为373.86 MPa，出现在锥壳小端与内筒连接区夹套筒体段。随翻边角度α的增大，在α=30°时最大应力位置转移至锥壳大端与夹套筒体连接过渡段外表面，为276.02 MPa，可推断出此时锥壳小端与内筒连接区应力得到了极大的缓解和降低，且降低幅度较大。随α的继续增大，最大应力值位置始终在锥壳大端与夹套筒体连接过渡段外表面，但最大应力值则逐渐减小（由α=30°时的276.02 MPa 减小到α=75°时的210.21 MPa）；另外，锥壳大端与夹套筒体连接过渡段高应力区仅局限于轴向Ⅰ、Ⅱ（图8b）局部区域，且I 区的应力值始终大于Ⅱ区，在远离Ⅰ、Ⅱ局部区域时应力值急剧衰减，在环向Ⅲ、Ⅳ区局部区域应力值远小于Ⅰ、Ⅱ区。

3.4 凹口锥翻边结构应力线性化后各类应力变化规 律

本节同样定义四条路径并对线性化后的薄膜应力、弯曲应力和峰值应力进行归类探讨其变化规律，线性化路径及路径下各类应力在不同翻边角度下的变化规律分别如图9、10 所示。

由图10a、b 分析可知：对于凹口锥大端与夹套筒体连接过渡段外表面Ⅰ区（Path 1），薄膜应力随翻边角度增大到α=30°时有显著增大趋势，当α继续增大时出现轻微下降趋势，在α=60°时则又开始有极小幅度增加趋势，弯曲应力变化趋势则与薄膜应力正好相反，峰值应力呈小幅增加后保持基本不变的趋势；Ⅱ区（Path 2）各类应力变化趋势总体与I 区相同，不同的是在α＞30°后薄膜应力和弯曲应力一直呈下降趋势。对比封口锥与凹口锥大端连接过渡段（Ⅰ、Ⅱ区）应力情况，不难发现，封口锥大端过渡段弯曲应力远大于薄膜应力，其大小和变化趋势对总应力值起决定作用。而凹口锥大端过渡段薄膜应力大于弯曲应力起主导作用，薄膜应力与弯曲应力的叠加共同决定总应力变化趋势。分析认为：对于凹口锥大端过渡段，其中一次总体薄膜应力仍占主导作用，但此处的一次薄膜应力值比封口锥过渡段处的要大很多，结构不连续导致的局部薄膜应力值仍较小且受翻边角度影响不大；一次和二次弯曲应力翻边角度增大到α=30°时显著得到改善和降低，峰值应力与封口锥过渡段（Path 1）趋势相同且很小。由图10c、d 分析可知：对于凹口锥小端与内筒体连接区（Path3、Path 4），随α的增大，薄膜应力、弯曲应力、峰值应力及总应力均呈下降趋势，在α=30°之前下降趋势较为显著，之后下降趋势变缓。对于连接处内筒（Path 3），薄膜应力极小，总应力主要由弯曲应力和峰值应力决定；对于连接处夹套筒体（Path 4），薄膜应力、弯曲应力和峰值应力大小相当，共同决定总应力的大小和趋势。分析认为：在Path 2 和Path 3 处，应力较大的原因主要是为满足变形协调而产生的二次弯曲应力和附加的峰值应力，不同的是在Path3 处为满足静力平衡还会产生较大的二次性质的局部薄膜应力。

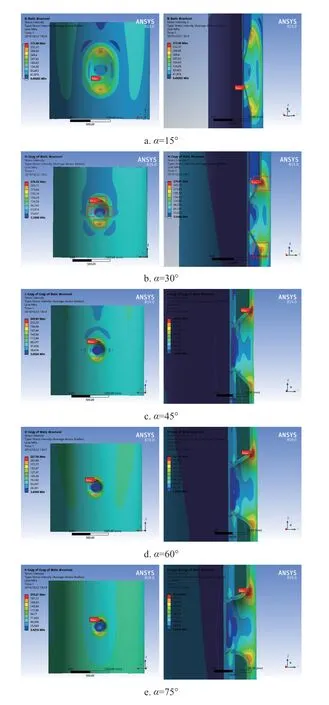
图8 凹口锥翻边结构在不同翻边角度下的应力变化趋势Fig.8 Stress distribution of notched-cone structure under different flanged-angle

图9 高应力区域线性化路径（Path 1 ～ Path 4）Fig.9 Linearized path at high stress region

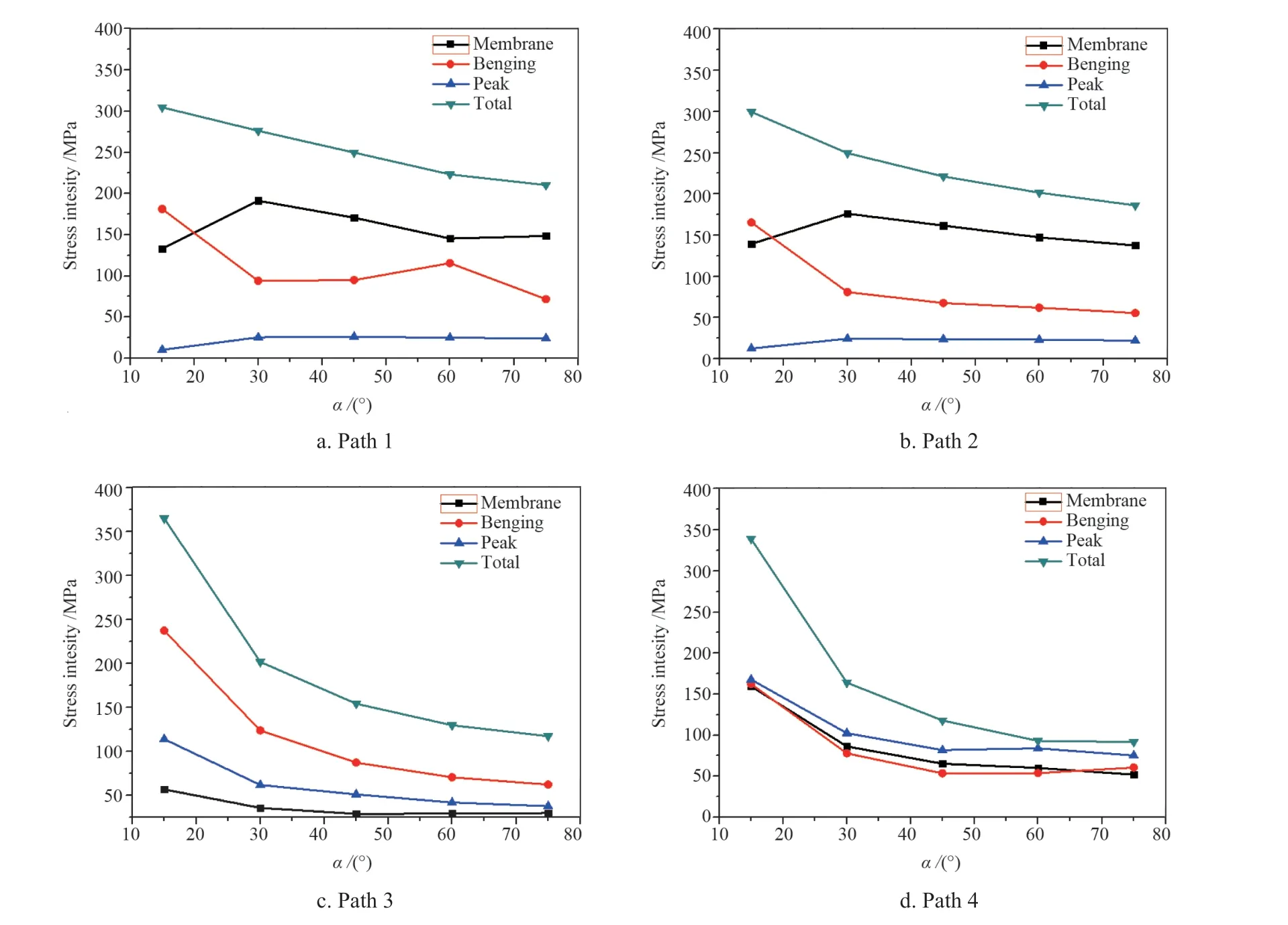
图10 线性化路径下各类应力在不同翻边角度下的变化规律Fig.10 Stress distribution under different flanged-angle at linearized path

4 结论

本文以某一反应釜工程实例，采用有限元分析法对其封口锥和凹口锥总体结构不连续处薄膜应力、弯曲应力、峰值应力及最大总应力受翻边角度影响的变化规律进行分析并探讨了各类应力产生的原因，基于本文计算模型和结果分析，最终得出结论如下[10]：

（1）封口锥和凹口锥翻边结构存在两个总体结构不连续导致的高应力区：一是锥壳大端与夹套筒体连接过渡段区，二是锥壳小端与内筒连接区。

（2）对于封口锥翻边结构：两个高应力区的最大应力值均随翻边角度α的增大而显著增大，且锥壳小端与内筒连接区的增幅远大于大端与筒体过渡区，在翻边角度增大到α=60°时，最大应力位置发生改变，且应力值逐渐显著增大。主要原因在于一次和二次弯曲应力起决定作用且随α的增大而急剧增大。

（3）对于凹口锥翻边结构：两个高应力区的最大应力值则随翻边角度α的增大而逐渐减小，在α＜15°时，最大应力出现在锥壳小端与内筒连接区的夹套筒体段，随α的增大，此处应力降低幅度较大，导致最大应力转移至大端与夹套筒体连接的I 区且逐渐减小。主要原因在于共同起决定作用的薄膜应力和弯曲应力随α的增大均有所减小。

（4）在满足工艺和结构要求的前提下，封口锥翻边结构建议采用翻边角度α=30° ～ 45°，但对应力比较敏感的设备（如低温工况、应力腐蚀工况、疲劳工况），应优先选用α=30°的翻边结构，受力状态比45°优越且能大幅降低应力值。另外，封口锥上一般会开设排气管，在α=30°时锥段较长，可增加小端与内筒连接区应力的衰减长度，避免与排气管开孔处应力叠加。

（5）在满足工艺和结构要求的前提下，凹口锥翻边结构建议采用翻边角度α=45° ～ 60°，同（4）对于应力比较敏感的设备，理论上选用α=60°的结构受力状态较好且应力值较低，但在α=45° ～ 60°区间，应力降低幅度并不显著；从制造方面，则α=45°的翻边结构更易于加工成型。综合受力和制造两方面分析，应优先选用α=45°的翻边结构。