基于内聚力法则的高能硝酸酯增塑聚醚推进剂开裂过程细观模型

2021-01-08侯宇菲许进升古勇军周长省

兵工学报 2020年11期

侯宇菲，许进升，古勇军，周长省

(1.南京理工大学机械工程学院, 江苏南京 210094; 2.山西北方兴安化学工业有限公司, 山西太原 030008)

0 引言

固体推进剂作为固体火箭发动机的能量来源，其结构完整性直接决定整体火箭系统及作战平台的安全。为保证高能的要求，固体推进剂中掺入了大量固体填料，因而形成了一种多相体(基体相、增强相、界面相)含能材料。这种多相材料在载荷作用下，将会引起颗粒与基体界面脱湿、裂纹扩展、变形等缺陷，其宏观力学性能由细观多尺度物理所决定[1-2]。因此，从细观角度出发研究细观结构对推进剂力学性能的影响，对于推进剂配方的研制具有科学的指导意义[3]。

近年来，国内外学者采用扫描电镜与数字图像相关方法对高能材料的细观结构演化进行观察，发现颗粒与基体的界面是多相材料失效的起点[4-5]。然而，由于实验手段的局限性，无法定量分析高能材料的细观损伤破坏演化过程，因此数值仿真法成为近年来兴起的分析多相材料界面破坏的有效方法。陈煜等[6]采用单颗粒轴对称细观模型对硝酸酯增塑聚醚(NEPE)推进剂在不同固含量、键合剂等作用条件下的应力集中因子及脱湿角进行了研究。Matous等[7]利用分子动力学方法生成推进剂细观代表性体积单元，研究了在小应变条件下颗粒界面的损伤与失效，证明了界面损伤是造成力学性能非线性的主要原因。Inglis[8]在Matouš的研究基础上，采用椭圆形颗粒进行数值计算，得知模型损伤演化过程分为3个阶段：弹性阶段、颗粒与基体界面脱湿和基体大变形。Cui等[9]通过实验得知推进剂的力学性能与加载速率相关，为更准确地描述推进剂在工作过程中的力学性能，建立了帕克- 保利诺- 勒斯勒尔(PPR)率相关粘聚区准则。Zhang等[10]通过不同温度及应变速率的单轴拉伸实验发现，只考虑推进剂颗粒与基体界面脱湿的数值仿真无法准确地预测推进剂的失效行为，以此推测推进剂的失效还包括基体的损伤。周水平等[11]采用原位扫描电镜得出推进剂的失效包括颗粒与基体界面脱湿与基体拉丝破坏。但以上方法都局限在颗粒与基体界面脱湿对推进剂力学性能的影响，尚未考虑基体失效对推进剂力学性能的影响。

本文针对复合固体推进剂细观损伤演化规律，建立同时考虑颗粒与基体界面脱湿与基体开裂的细观颗粒填充模型，并采用VUMAT子程序编译出多项式- 梯形内聚力法则，分别与双线性、多项式内聚力法则进行对比研究，得出更符合高能NEPE推进剂开裂过程的细观颗粒模型。

1 NEPE推进剂细观颗粒模型

1.1 细观颗粒填充模型

本文以NEPE推进剂为研究对象，其本构关系通过准静态单轴拉伸实验获取，单轴拉伸实验在QJ万能材料试验机上进行。该NEPE推进剂的主要成分包括铝(Al)粉、高氯酸铵(AP)及其他辅助制剂，各组分含量如表1所示。通过分子动力学算法[12]生成与复合固体推进剂具有相同体积分数的细观颗粒填充模型，其中Al粉粒径为8～20 μm，AP(1)的粒径为100～120 μm，AP(2)的粒径为250～300 μm，粒径分布如图1所示。

表1 NEPE推进剂基本组分Tab.1 Components of NEPE propellant

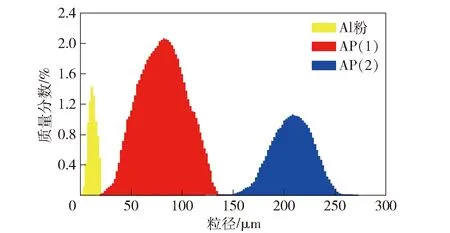
图1 NEPE固体推进剂颗粒粒径分布Fig.1 Particle size distribution of NEPE propellant

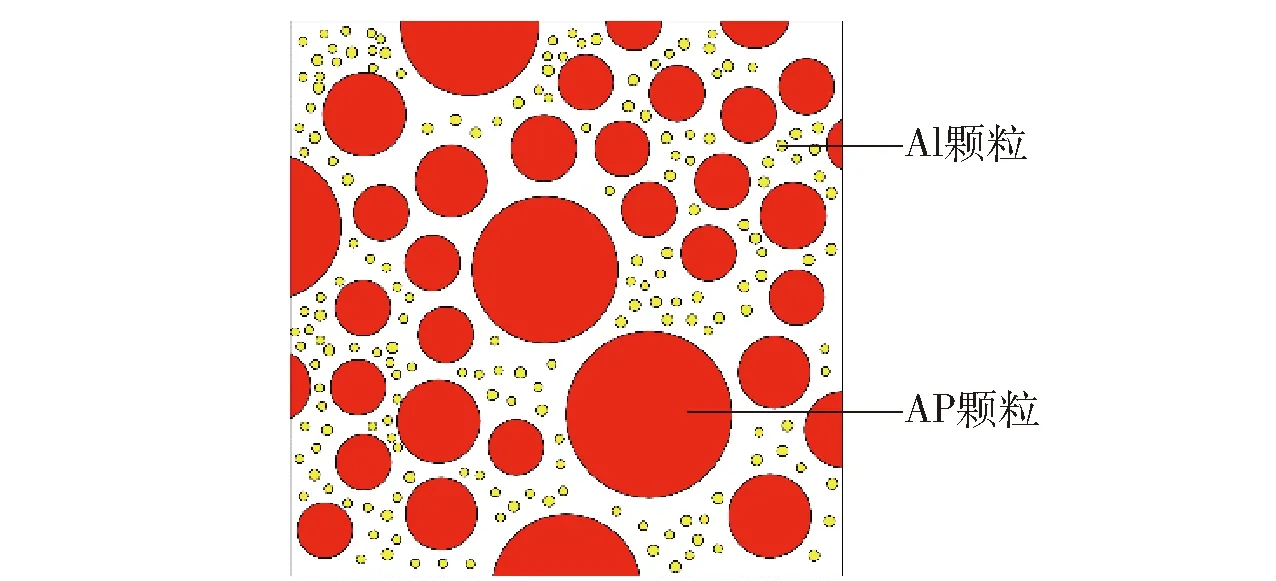
图2 NEPE固体推进剂颗粒填充几何模型Fig.2 Particle packing model of NEPE propellant

根据文献[13]得知，当代表性体积单元的尺寸为最大粒径尺寸的3～5倍时，则认为代表性体积单元有效。因此，本文根据图1填充颗粒粒径分布规律得到推进剂细观颗粒模型的代表性体积单元，如图2所示，其尺寸为1 000 μm×1 000 μm. 由于Al粉颗粒的粒径小且数量多，若直接对该模型进行网格划分，将会降低网格质量并影响计算结果的收敛性。文献[14]通过实验证明，Al颗粒作为加速复合推进剂热分解的添加剂，不会引起颗粒与基体界面脱湿。因此采用Mori-Tanaka解析法[15]将Al颗粒对推进剂力学性能的影响等效到基体中，在计算时只考虑AP颗粒的影响。材料参数如表2所示。

表2 细观材料力学属性Tab.2 Mechanical properties of meso-components

1.2 粘结单元

粘结单元的基本思想是构造一种可以赋予材料损伤特性的特殊单元，其力学行为遵循内聚力法则的力学响应，当粘结单元与有限元模型结合后，实现模型的失效破坏。本文利用Python脚本语言在颗粒与基体界面及基体内部嵌入零厚度粘结单元，实现NEPE推进剂颗粒与基体界面脱湿至基体断裂的过程。具体如下：

1) 将颗粒填充模型导入Abaqus软件中，分别建立基体单元集合与颗粒单元集合，采用四节点的平面应变单元对以上集合进行网格划分，其网格类型为CPE4，并以Abaqus软件inp格式输出。

2) 遍历整个模型集合，划分颗粒单元与基体单元的公共节点及基体单元内部公共节点，并建立新的单元集合。如图3(a)所示，深色部分为AP颗粒单元，浅色部分为基体单元。

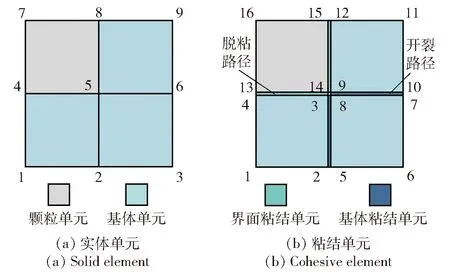
图3 粘结单元插入示意图Fig.3 Schematic diagram of embedded cohesive elements

3) 将所有公共节点拆分并重新编号，保留新旧节点坐标对应关系，如图3(b)所示，节点4被拆分为节点4和节点13，节点6被拆分为节点7和节点10.

4) 基于新旧节点坐标对应关系，对颗粒单元和基体单元重新编号并生成粘结单元，粘结单元编号时必须按逆时针方向编号，其网格类型为COH2D4. 粘结单元分布如图3(b)所示，在实际计算过程中粘结单元的几何厚度为0 mm.

5) 生成新的inp文件，为方便后续添加材料属性，建立4个集合放置4种不同材料属性的单元：AP颗粒单元集合，基体单元集合，界面单元集合，基体粘结单元集合。

1.3 边界条件

为模拟NEPE推进剂在单轴等速拉伸下的细观失效过程，需对所建立的细观颗粒填充模型选用合理的边界条件，为满足细观模型周期性及材料均匀性假设，通常对代表性体积单元施加周期性边界条件。然而，周期性边界条件在实现过程中依赖于周期性网格，不适用于 NEPE推进剂的复杂细观结构。文献[16]表明，只要代表性体积单元的尺寸适当，均匀位移边界条件可替代周期性边界条件。因此本文选用均匀位移边界条件，具体施加方式如图4所示。

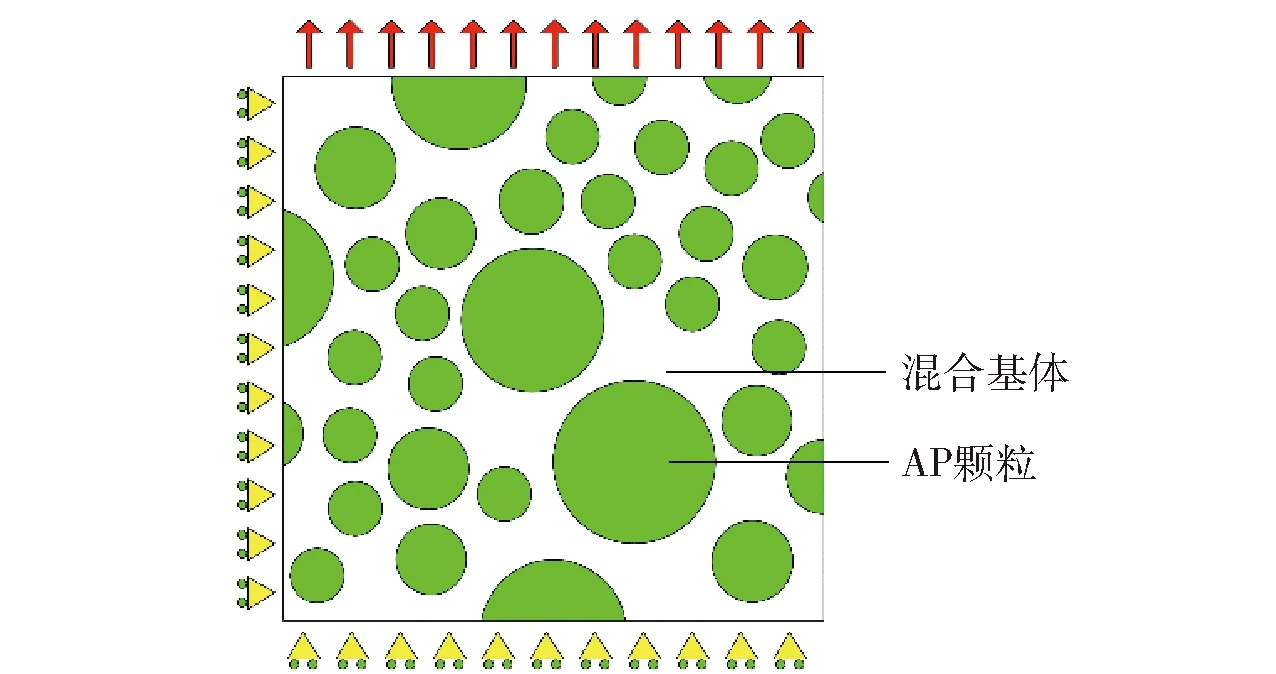
图4 NEPE推进剂细观模型边界条件施加Fig.4 Boundary conditions of mesoscopic model of NEPE propellant

2 多项式- 梯形内聚力法则的建立

2.1 双线性内聚力法则

20世纪60年代，Barenblatt[17]和Dugdale[18]针对断裂力学中裂纹尖端的应力奇异性问题，首次提出了内聚力法则，内聚力模型如图5所示。内聚力区域的力学状态通过最大断裂强度σmax、界面临界张开位移δ0和断裂能φ确定[19]。其中，双线性内聚力法则最为常见，如(1)式所示：

(1)

式中：T为断裂强度；σ为张开位移；δf为特征位移。

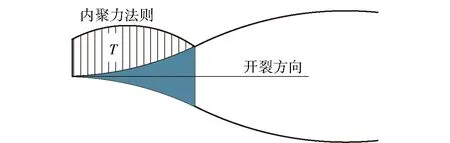
图5 内聚力模型示意图Fig.5 Schematic diagram of real fracture process of cohesive zone model

最大断裂强度σmax与界面临界张开位移δ0的比值为模量K. 先前研究者认为内聚力法则中的参数最关键，而曲线形式是次要的。但是，文献[20]在研究铬与锆钛酸铅(Cr/PZT)界面开裂时发现，双线性内聚力法则能够与实验结果匹配，而指数型的仿真结果较差。

2.2 多项式- 梯形内聚力法则

针对NEPE推进剂复杂的力学行为，所选用的内聚力法则必须同时满足高断裂能和张力位移非线性损伤特点。对于双线性内聚力法则而言，若想增加断裂能，则必须提高断裂强度或临界开裂位移，而断裂强度或临界开裂位移的增加会引起应力值增大或界面无法开裂的现象。为解决张力位移非线性问题，Tvergaard等[21]在研究弹塑性材料破坏时提出梯形内聚力法则，这种内聚力法则有效地提高了断裂能，更好地描述了材料的塑性损伤阶段。然而梯形内聚力法则的上升段、下降段均为线性函数，并不适用于表征NEPE推进剂材料非线性张力位移关系(通常只有5%的弹性阶段)。

Needleman等[22]为解决张力位移非线性问题，建立了多项式内聚力法则，与双线性内聚力法则、梯形内聚力法则不同，其张力位移关系为连续性方程，需要通过断裂能控制方程求偏导得到。二维平面状态下的多项式内聚力模型断裂能方程为

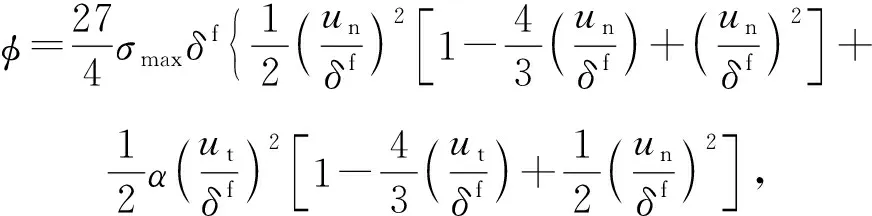
(2)

式中：un和ut为法向与切向的临界界面位移分离值；α为法向刚度与切向刚度的比例系数。

(2)式求导，可得

(3)

(4)

式中：Tn和Tt分别为法向和切向的断裂强度。

为同时满足推进剂材料的延展性损伤特点和张力位移非线性变化关系，本文建立了多项式- 梯形内聚力法则，将多项式与梯形内聚力法则用分段函数表示，应力的上升段和下降段为多项式函数，应力屈服段为常数，如图6所示，并通过VUMAT子程序完成了该法则的数值开发，可更准确地描述NEPE推进剂的力学性能。

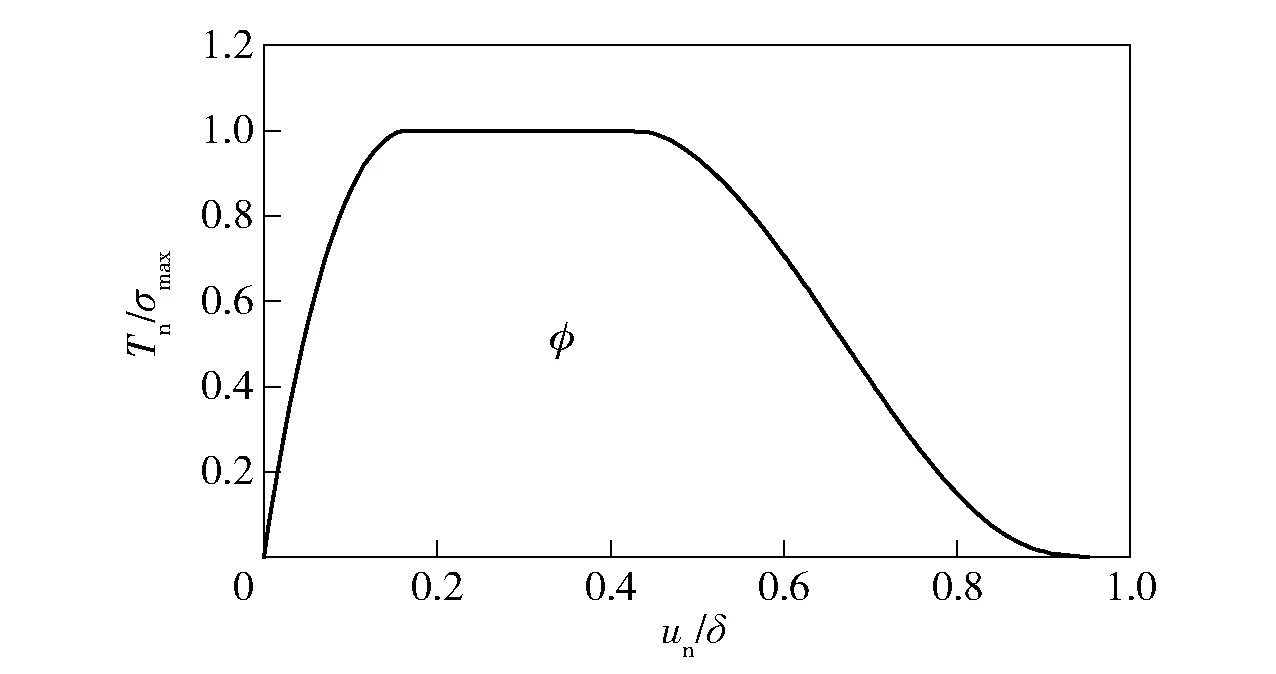
图6 梯形- 多项式内聚力法则Fig.6 Trapezoidal-polynomial cohesive law

多项式- 梯形内聚力法则的位移与张力控制方程为

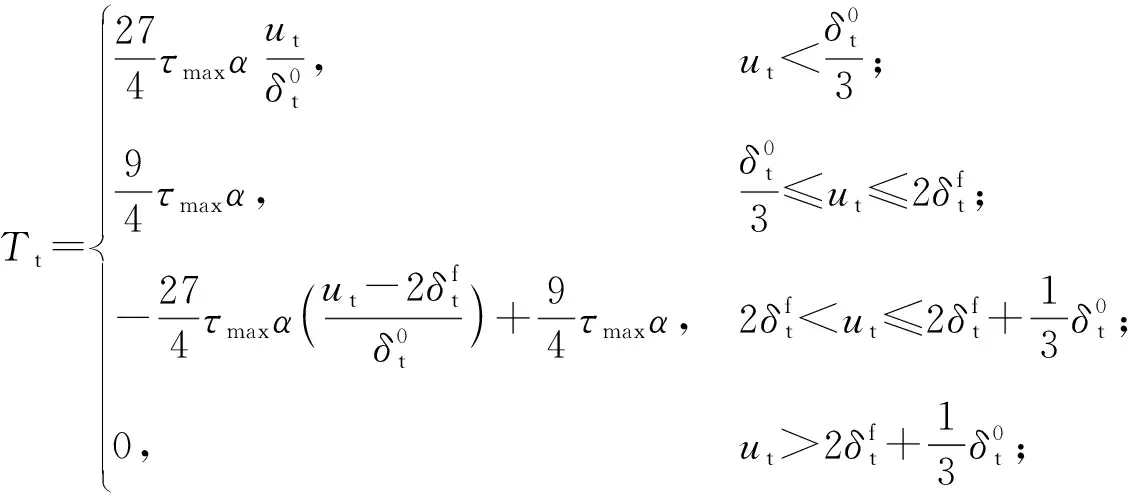
(5)

(6)

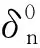
断裂能φ控制方程为

(7)

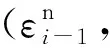
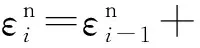
(8)

由(8)式计算各向应力σ：

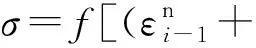
(9)

式中：T0为粘结单元计算厚度。

subroutine vumat()

Input:

Smax !断裂强度

Disnn !延性损伤位移

Distn !特征位移

Do 100i=1, nblock

Compute(stress, strain, displacement, energy)

Improvement(stress, strain, displacement, energy)

If (stateNew(error)==0) then

stateNew(delete)=0

else

stateNew(delete)=1

end if

100 continue

Return

End

图7 多项式- 梯形内聚力法则算法

Fig.7 Trapezoidal-polynomial cohesive law algorithm

为实现粘结单元的损伤演化至失效过程，通过设置状态变量SDV(stateNew)判断粘结单元的失效，当状态变量由1变为0时，粘结单元进行不可逆删除。

2.3 参数反演识别

对于内聚力法则参数获取方法，现阶段很难直接由实验获得。本文采用反演分析法获得内聚法则的材料参数。以实验曲线上数据点的位移值为基准，在仿真曲线上找到最靠近该基准点的最小区间，随后在最小区间的两个端点间线性插值得到仿真值，最后利用目标函数得到实验值与仿真值的最小误差R(具体步骤见文献[23])：

(10)

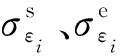
本文分别对双线性内聚力法则、多项式内聚力法则和多项式- 梯形内聚力法则进行参数反演识别，并假设推进剂为各向同性材料，内聚力法则的法向参数与切向参数相同，反演后的参数如表3～表5所示。

表3 双线性内聚力模型参数Tab.3 Parameters of bilinear cohesive zone model

表4 多项式内聚力模型参数Tab.4 Parameters of polynomial cohesive zone model

表5 多项式- 梯形内聚力模型参数Tab.5 Parameters of polynomial-trapezoidal zone model

3 推进剂开裂过程细观仿真及失效分析

3.1 网格收敛性

为消除有限元模型的物理离散误差，有必要对其进行网格收敛性检查。通过减小单元尺寸即提高插值函数的阶次，使有限元模型的解收敛于精确解。同时为确保粗网格的计算结果是定性正确的，粗网格的尺寸Δy不宜过大，并且不同网格尺寸Δy的比值c保持一致，即

(11)

图8给出了4种网格尺寸Δy的有限元模型。下面对颗粒与基体界面为双线性内聚力法则的细观颗粒填充模型施加微小载荷，采用有限元计算获得初始弹性模量，与实验弹性模量作对比，获得最精准的网格尺寸。

图8 NEPE推进剂网格示意图Fig.8 Schematic diagram of NEPE propellant mesh

如图9所示，随着网格尺寸的减小，有限元模型的初始弹性模量逐渐趋于稳定并接近于实验值，表明实体单元阶次对计算结果的影响随网格尺寸减小而逐渐降低。当网格尺寸Δy=0.02 mm时，初始模量E0的计算结果收敛，因此采用该网格尺寸作为本文相关模型的网格尺寸标准。

3.2 推进剂脱湿细观仿真及分析

为证明NEPE推进剂细观应力场的分布与内聚力法则的曲线形式有关，下面采用不同曲线形式的内聚力模型对NEPE推进剂细观颗粒填充模型的损伤演化过程进行分析。其中：模型1为颗粒与基体界面采用双线性内聚力法则；模型2为颗粒与基体界面采用多项式内聚力法则；模型3颗粒与基体界面采用多项式- 梯形内聚力法则。

表6分别给出了模型1、模型2、模型3应变为8%、24%、34%、50%时的应力云图及损伤演化情况。当应变为8%时，颗粒与基体之间未出现明显的位移分离，界面粘结性能良好。但由于颗粒与基体刚度严重不匹配，导致模型内部应力分布极不均匀，颗粒应力明显高于基体应力，表明模型的整体应力强度因AP颗粒而提高。当应变增加到24%时，大颗粒与基体之间发生位移分离，这是因为颗粒刚度远大于基体刚度，随着应变的增加，基体的变形远大于颗粒的变形，导致颗粒与基体界面成为整个模型中最薄弱的环节，即颗粒与基体之间出现位移分离的现象。当应变为34%时，基体变形增大，颗粒与基体的位移分离量增加，导致颗粒从孔洞中裸露出来进而形成脱湿。当应变达到50%时，模型中颗粒与基体界面脱湿数量持续增加，直至所有颗粒与基体的界面都消失。

由表6可知，3个模型的损伤演化过程相同，但应力值分布不同，表明模型应力分布和内聚力法则的曲线形式有关，但单从应力云图无法判断哪一种内聚力法则更适合描述NEPE推进剂的颗粒与基体界面失效过程。

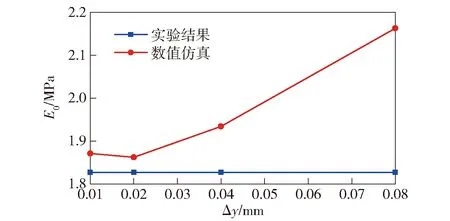
图9 NEPE推进剂网格- 初始弹性模量曲线Fig.9 NEPE propellant mesh-initial elastic modulus

3.3 推进剂脱湿损伤分析

图10所示为实验应力- 应变曲线。从图10中可以发现，NEPE推进剂的力学特性曲线可分为4个阶段：线性段、软化段、下降段和断裂破坏段。在线性段，应力随应变的增加而线性增加，此时推进剂性能保持完整，尚未发生损伤。当到达软化段时，应力- 应变曲线出现拐点(即A点处)，曲线斜率缓慢降低，材料的模量开始下降，结合应力云图发现此时颗粒与基体界面发生了位移分离。在下降段，应力随应变的增加而快速降低，曲线的斜率进一步降低。在断裂破坏段，应力随应变增加而缓慢增加，当跨过应力平台区后，应力快速下降，形成断裂。

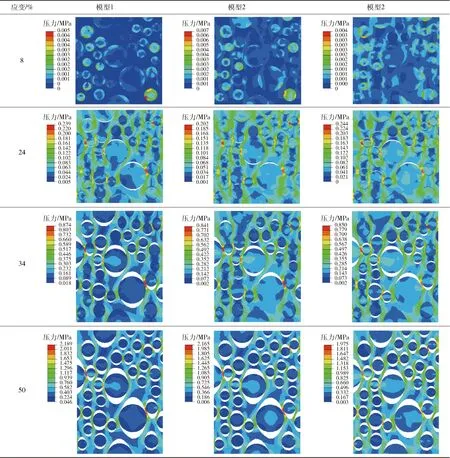
表6 NEPE推进剂Mises应力云图

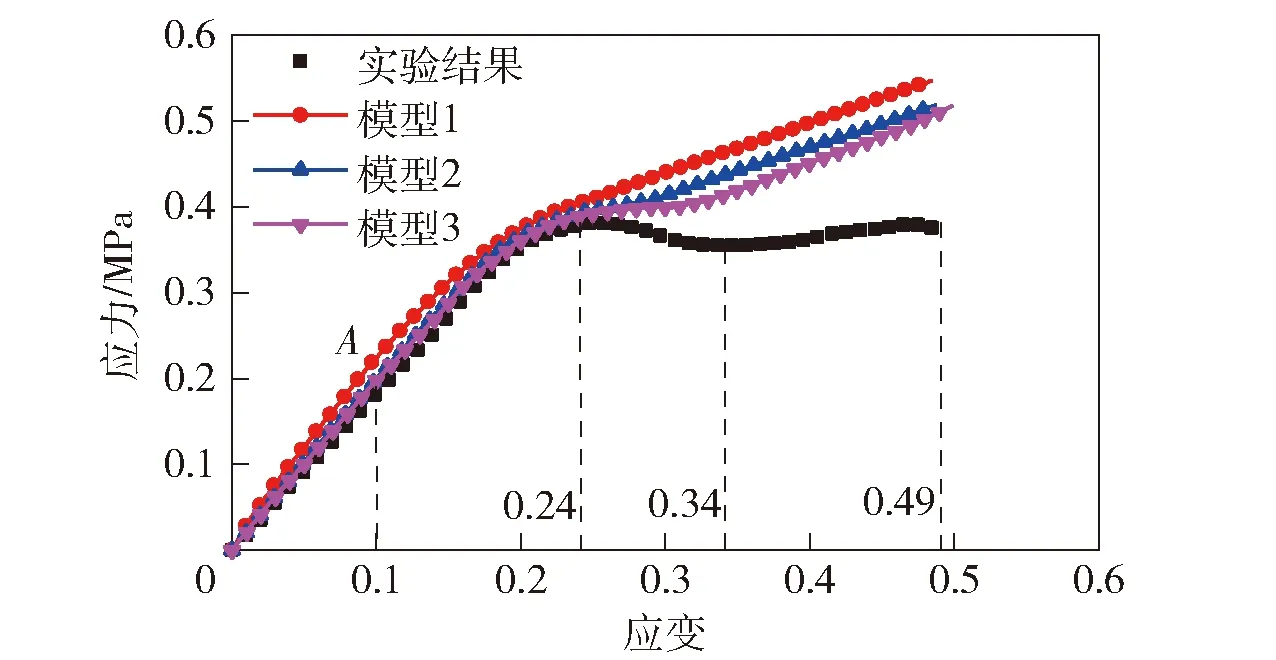
图10 NEPE推进剂应力- 应变曲线Fig.10 Stress-strain curves of NEPE propellant

对比预测结果与实验结果得知，在应力- 应变曲线的线性段，3种模型的仿真曲线与实验曲线完全拟合。当到达软化段时，模型2与模型3预测结果较好，模型1的应力值偏高。这是因为双线性内聚力法则与多项式内聚力法则的损伤变量形式不同，在双线性内聚力法则中，只有当材料点的应力值到达断裂强度时模型才开始损伤，而多项式内聚力法则的损伤是从载荷施加的起点开始迭代，因此多项式内聚力法则表征的颗粒与基体界面刚度软化较快。当3种模型处于下降段和断裂破坏段时，其预测结果均偏离实验结果，模型1和模型2的应力随着应变的增加而增加，模型Ⅲ经过一个微小的应力平台区后，其应力值也随即增大，最终3种模型的应力值均为发生下降。由此可知，颗粒与基体界面脱湿只能造成推进剂模量的下降，并不会引起推进剂的失效破坏。因此，只考虑颗粒与基体界面损伤的细观颗粒模型并不能完整地预测推进剂的力学性能。

3.4 推进剂开裂过程细观仿真及分析

通过3.2节得知，仅考虑颗粒与基体界面脱湿的细观颗粒模型并不能完整地预测NEPE推进剂的宏观力学性能，因此下面采用考虑基体失效的细观颗粒填充模型进行数值仿真，其中：模型4为颗粒与基体界面及基体内部采用双线性内聚力法则；模型5为颗粒与基体界面及基体内部采用多项式内聚力法则；模型6为颗粒与基体界面及基体内部采用多项式- 梯形内聚力法则；模型7为颗粒与基体界面采用多项式内聚力法则，基体内部采用多项式- 梯形内聚力法则。

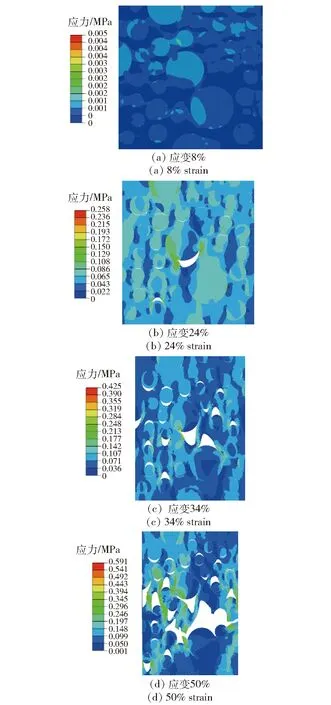
图11 应变分别为8%、24%、34%、50% 时NEPE 推进剂Mises应力云图Fig.11 Mises stress nephograms of NEPE propellant at the strains of 8%, 24%, 34%, and 50%

由于模型数量较多，并且各个模型的云图变化过程相似，下面只给出模型7在应变为 8%、24%、34%、50%时的应力云图，如图11所示。当应变为8%、24%、34%时，其仿真结果与3.2节的仿真结果相同，表现为未损段、颗粒与基体产生位移分离段和颗粒与基体界面脱湿段。然而，当应变达到50%时，未考虑基体失效与考虑基体失效的细观颗粒填充模型其应力云图产生明显区别，如图10与图11所示。考虑基体失效的细观颗粒填充模型其颗粒与基体界面脱湿数量维持水平，部分孔洞发生汇聚，导致基体内部形成微裂纹。而未考虑基体失效的细观颗粒填充模型，其颗粒与基体界面脱湿数量持续增加，模型内部未出现微裂纹。通过文献[10]得知，考虑基体失效的细观颗粒填充模型其预测结果和实际情况相符，并且裂纹方向与载荷加载方向相垂直。这是因为在未考虑基体损伤的模型中，虽然颗粒与基体界面脱湿导致基体内部形成高应力区，但由于基体未考虑损伤，高应力区域无法形成裂纹，模型整体即可持续拉伸，直至所有颗粒与基体界面都脱湿。而考虑基体损伤的模型中，当颗粒与基体界面脱湿后，基体成为载荷承担主体，在承载的初始阶段应力随着应变增加而小幅度增加，但由于颗粒与基体界面脱湿后产生了大量的孔洞，在与载荷方向相垂直的孔洞处形成了高应力区，随着载荷的持续加载，高应力区迅速形成裂纹。当裂纹产生后未脱湿区的应力值转而降低，因此颗粒与基体界面脱湿数量维持恒定。

3.5 推进剂断裂损伤分析

通过上述分析得知，颗粒与基体界面脱湿引起基体内部产生高应力区是造成推进剂破坏的关键，因此基体损伤不容忽略。与3.3节的结果相似，以上4个模型的损伤演化过程相同，但应力值分布不同，因此下面通过细观模型预测应力- 应变曲线与实验应力- 应变曲线来验证模型的准确性。

如图12所示，考虑基体失效的细观颗粒填充模型可以完整地模拟出NEPE推进剂力学曲线变化的4个阶段。在线性段和软化段，采用多项式内聚力法则的细观颗粒填充模型，其预测结果与实验结果更为接近。在下降段，模型6、模型7较模型4、模型5的应力值下降更为缓慢，更接近实验结果。在断裂破坏段，模型4和模型5的应力随应变的增加而增加，当到达应力峰值后快速断裂，期间并未出现应力平台区；而模型6和模型7的曲线走势基本和实验结果相一致，当跨越一个缓慢上升的应力平台区后快速断裂。

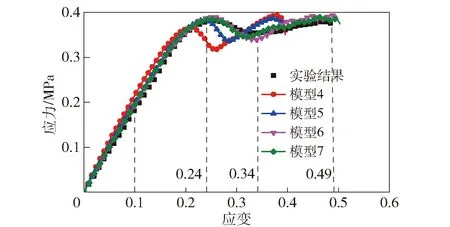
图12 NEPE推进剂应力- 应变曲线Fig.12 Stress-strain curves of NEPE propellant

通过上述分析得知，模型6和模型7的仿真结果与实验结果最为接近。这是因为：1)多项式内聚力法则中的张力位移为非线性变化，更适合描述NEPE推进剂颗粒与基体界面脱湿的实际损伤过程；2)NEPE推进剂基体材料变形较大，采用多项式- 梯形内聚力法则可以有效地模拟出推进剂在拉伸过程中的应力平台区，并提高模型的断裂能，而双线性内聚力法则更适合描述脆性材料的损伤，无法体现推进剂材料延展性损伤的特点。

在图12中，模型6和模型7的仿真结果略高于实验结果，分析误差产生的原因，有以下3种：1)本文推进剂的细观模型是二维的，网格的单元类型均基于平面应变，与真实推进剂的三维应力与应变状态存在一定区别；2)目前，为简化模型，将填充颗粒均设置为圆形颗粒，但在真实结构中颗粒的形状是类似于圆形的；3)真实推进剂在固化搅拌过程中，颗粒与基体界面存在一定缺陷，而在本文模型中，认为颗粒与基体之间是完全粘结在一起的，不存在任何缺陷。这些原因均使得仿真结果偏高。