基于交叉效率排序多目标进化算法的备件供应优化

王亚东， 石全， 尤志锋， 王芳， 夏伟，2

(1.陆军工程大学石家庄校区 装备指挥与管理系, 河北 石家庄 050003；2.陆军步兵学院石家庄校区 机械化步兵系, 河北 石家庄 050083)

0 引言

充足及时的备件供应是维修工作顺利开展的前提，也是装备保障工作的重中之重。备件供应优化和方案决策需要综合考虑时间、风险、成本等多方面因素，优化目标多元，建模和求解难度较大[1]。因此备件供应网络优化和供应方案决策始终是备件保障的重点和难点问题。

目前很多学者对备件供应优化开展了相关研究。魏国强等对需求点的优先级聚类排序，研究了资源不足情况下的备件调度模型，以供应开始时间最早和调运线路最少为目标建立模型，并通过赋权将多目标转化为单目标优化进行求解[2]。刘喜春等建立了典型3级备件供应保障结构下的战时多阶段备件供应保障规划模型，以期望缺件量为目标建立无约束单目标优化模型，通过迭代方法获得备件供应保障优化策略[3]。张斯嘉等建立了基于可信性理论的战时多目标保障物资供应优化模型，采用蝙蝠算法求解多目标优化问题[4]。秦进等以最小化系统成本为目标，考虑应急资源数量、备用容量和位置数量等约束，建立了考虑服务可靠性的应急资源布局优化模型，提出一种基于矩阵实数编码的遗传算法求解方法[5]。Fazli-Khalaf等以最小化设施之间的总供应成本和运输时间，同时最大化供应可靠性为目标，建立了应急供应三目标优化模型[6]。Zhang等以最大限度地减少运输时间、运输成本和不满足度为目标，建立了多目标三阶段随机规划模型，采用基于隶属度模糊辅助变量的替代单目标模型来处理多目标模型[7]。Mohammadi等以最大化总预期需求覆盖、最小化总预期成本并最小化节点之间满意率为目标，建立了一个多目标随机规划模型，并采用多目标粒子群优化算法来解决这个模型[8]。Su等以完全响应时间和紧急资源成本为目标构建双目标乘法约束整数线性规划模型，并使用差分进化算法搜索模型的最优解[9]。综上所述可以看出，目前相关研究大多采用多目标优化模型。这是因为单目标优化的优化目标单一，考虑因素较少，不适于备件供应优化决策。但是，多目标优化求解难度大且得到的是一系列非支配解集，无法确定唯一的最优方案，因此不利于进一步决策。

本文为解决备件供应优化决策问题，以供应时间、风险、成本为目标，构建备件供应多目标优化模型。在求解算法上，本文受到了带精英策略的非支配排序遗传算法(NSGA-II)的启发，在多目标进化算法(MOEA)的基础上，采用交叉效率数据包络分析(DEA)对存档中的非支配解进行排序。一方面，可以指导种群向最优效率个体进化；另一方面，可以计算得到非支配解的自评效率和互评效率值，从而对众多非支配解进行排序、决策出最优解。

1 备件供应多目标优化模型

1.1 问题描述

某备件供应网络由后方仓库、野战仓库和用装单位3级节点组成。用装单位的维修力量对损坏装备进行维修时产生备件需求。后方仓库为备件的供应点，考虑到安全问题，通常距离任务前线相对较远。因此在后方仓库和用装单位之间设置野战仓库，野战仓库通常靠前设置，接收后方仓库供应的备件并前送至用装单位。备件供应优化则是根据备件需求、节点以及供应网路的状态信息确定最佳的备件供应方案，从而保证以较短的时间、较低的总风险和较少的成本满足备件需求。

本文备件供应模型建立在以下假设之上：1)以某类关键备件为研究对象。2)节点之间的备件运输成本和运输时间已知且为定值，节点之间运力充足。3)野战仓库的开放费用、库存费用、最大储备量均为已知且为定值。4)备件未能满足用装单位需求而造成的后果用缺件损失表示，缺件损失越大的用装单位表明其优先级越高；用装单位的备件需求量和缺件损失已知。5)备件全部到达野战仓库后再统一向用装单位进行分配和供应。6)供应网路的中断风险仅发生在野战仓库和用装单位之间。7)暂不考虑越级供应以及同级之间横向供应的情况。

1.2 变量及其说明

i：后方仓库的序号，i=1，2，…，I，I为后方仓库的数量；

j：野战仓库的序号，j=1，2，…，J，J为野战仓库的数量；

k：野战仓库的序号，k=1，2，…，K，K为用装单位的数量；

Uj：第j个野战仓库最大容量；

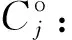
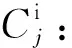
dk：第k个用装单位的备件需求量；

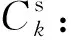
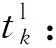
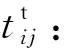
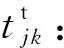
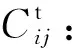
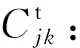
Rij：备件从后方仓库i运至野战仓库j的中断风险，假设中断发生在途中；

Rjk：备件从野战仓库j运至用装单位k的中断风险，假设中断发生在途中；

xij：后方仓库i向野战仓库j供应备件的数量；

xjk：野战仓库j向用装单位k供应备件的数量；

yj：二进制变量，用来标注野战仓库j的开放情况，yj=1表示开放，yj=0表示关闭。

1.3 模型建立

目标函数1：备件供应的总时间最短。

(1)

目标函数2：备件供应的总风险最低。

(2)

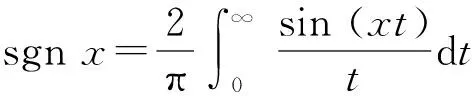
目标函数3：备件供应总成本最小。

minC=Co+Ct+Ci+Cs,

(3)

式中：Co表示野战仓库的开放成本；Ct表示运输成本；Ci表示备件在野战仓库的库存成本；Cs表示缺件损失。各项成本计算如下：

(4)

(5)

(6)

(7)

满足以下约束：

(8)

(9)

(10)

(11)

(12)

xij∈N+,xjk∈N+,yj={0,1}.

(13)

式中：N+为正整数。约束(8)式、(9)式表示未开放的野战仓库不参与备件供应，同时还规定了供入的备件数量不能超过野战仓库的最大容量；约束(10)式规定了用装单位的备件需求应得到满足；约束(11)式规定了野战仓库备件的供出量应不超过供入量；约束(12)式规定了对于每个用装单位，备件供应的延迟时间应不超过允许的最大截止时间。这里规定的延迟时间与目标函数中的总供应时间有所区别。供应总时间用来体现调运车辆数量和总里程等信息，而延迟时间则表示备件从供应开始到全部到达所消耗的时间；约束(13)式规定了决策变量的类型和取值范围。

2 二次目标交叉效率排序多目标进化算法

为了求解备件供应多目标优化模型的最优解以及得到最终方案，本文提出了一种二次目标交叉排序多目标进化算法(SGCES-MOEA)。该算法采用进化计算的基本框架，在每次迭代中将种群中的非支配解放入存档，并从存档中选择精英个体指导种群的进化。与传统进化计算不同的是，SGCES-MOEA采用了类似于NSGA-Ⅱ的排序机制来选择精英个体。NSGA-Ⅱ先根据种群中个体被支配的次数对个体分层，再对同一层的个体计算拥挤度距离，并根据拥挤度距离对每一层个体进行排序。第一层为非支配解(被支配次数为0)，该层拥挤度距离最大的个体为精英个体[10]。

SGCES-MOEA从NSGA-Ⅱ得到启发，用非支配个体的效率值代替拥挤度距离进行排序，从而选择出精英个体。相对于拥挤度距离，效率可以反映出个体在优化模型中的综合指标，具有实际意义。个体的效率值计算则采用改进的DEA法。每个非支配个体相当于一个决策单元(DMU)，根据优化模型计算得到各指标值后，再利用DEA评估模型计算个体的效率值。SGCES-MOEA的基本步骤如图1所示。

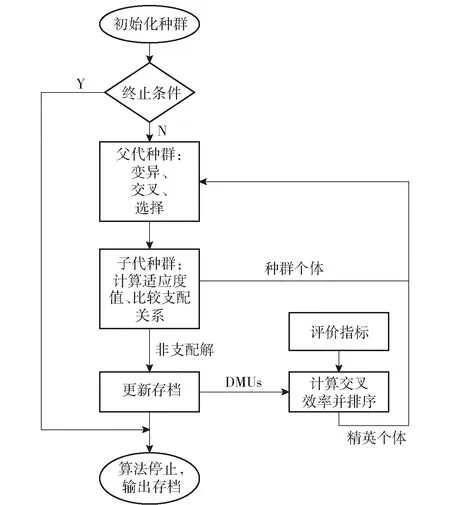
图1 SGCES-MOEA的基本流程Fig.1 Basic flow chart of SGCES-MOEA

2.1 进化策略

进化策略是对父代种群个体进行的变异、交叉、选择等操作，从而产生子代种群的过程。通过进化，种群不断得到改善，从而获得较优解。

步骤1变异。令ps=ps1,ps2,…,…,psh,…,psD为第s个父代个体向量，psD为第s个个体向量ps上的第D个变量；vs=vs1,vs2,…,…,vsh,…,vsD为根据变异策略产生的变异个体向量，vsD为第s个变异个体向量vs上的第D个变量。本文采用DE/current-to-best/1策略进行变异：

vs=ps+F×(pe-ps)+F×(pr-ps)，

(14)

式中：pe为当前种群中的最优个体；pr为从存档中随机选取的个体，且ps≠pe≠pr；F为变异率。

(15)

式中：rsh为[0,1]之间均匀分布的随机数；CR为交叉率，CR∈[0,1]，即当变异个体vs上第h个变量vsh对应的随机数小于交叉率时，交叉个体向量us上对应变量ush取父代个体ps对应变量xsh，否则保留变异个体上的变量值。

步骤3选择。根据种群中的父代个体和交叉个体的适应度函数，一一比较其支配关系。若某父代个体被对应的交叉个体支配，则用该交叉个体替换对应父代个体。最终得到的个体构成选择个体种群，作为子代个体进入下一次迭代。

步骤4更新存档。将子代种群中的非支配解放入存档中，与存档个体混合后，再次比较支配关系，选出混合种群的非支配解作为新的存档。

2.2 适应度函数及编码

由于本文构建的多目标优化模型属于带约束的优化问题，本文采用动态罚函数法处理模型约束[11]：

(16)

式中：x为决策变量向量；f(x)为适应度函数；O(x)为目标函数；M0为初始惩罚因子；ni为当前算法迭代次数，maxni为算法最大迭代次数；MK为惩罚系数；P(x)为约束违反度，

(17)

m为约束条件的总个数，ch(x)为约束违反度。若不等式约束表示为lh(x)≤0的形式，其约束违反度ch(x)=max(0,lh(x))；若等式约束表示为hh(x)=0的形式，其约束违反度ch(x)=max (0,|hh(x)-ε|)，ε为一个很小的实数。

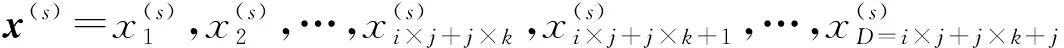
如图1所示，取直径为170 mm，直径偏差范围为0～0.8 mm的带轮进行实验。对带轮边缘轮廓进行测量，通过双目视觉圆弧轮廓特征提取和匹配之后，得出边缘外轮廓点的空间三维坐标。图2所示为求得的带轮边缘外轮廓点云图及空间圆弧拟合图，共获得266个边缘外轮廓点的三维坐标。利用本文拟合优化方法，对上述点云进行8次拟合，平均迭代数为6 895次。拟合结果如表1所示。

2.3 指标计算

根据DEA模型指标的性质，将评价指标分为输入型指标和输出型指标，输入型指标的值越小、对应DMU的效率越高，输出型指标的值越大、DMU的效率越高。

本文的输入型指标包括：

1)供应成本：计算公式即目标函数(3)式；

2)供应时间：计算公式即目标函数(1)式；

3)约束违反度：由于模型还涉及容量以及流量平衡等约束，将优化结果的约束违反度作为指标之一。模型的总体约束违反度计算公式为(17)式。

输出型指标包括：

图2 个体编码方式示意Fig.2 Chromosome individual coding pattern

1)可靠性指标：用备件供应的风险衡量，其值为总风险的倒数。风险计算公式为目标函数(2)式；

2)时效性指标：用延迟时间即供应开始到最后一波备件到达的时间衡量，取延迟时间的倒数。延迟时间的计算公式为约束(12)式；

3)满足度：用各用装单位的备件满足度表示，计算公式即约束(10)式。

2.4 二次目标交叉效率排序

算法采用DEA模型计算个体效率。传统DEA由Cooper等提出，其构建的固定规模收益的CCR模型[12]如下：

(18)

(19)

μra≥ε,υba≥ε,r=1,2,…,so,b=1,2,…,mi.

(20)

式中：Edd表示DMUd的自评效率，DMUd为第d个DMU；r为输出指标序号；so为输出指标的总个数；Yrd表示DMUd的第r个输出指标；mi为输入指标的总个数；μrd为Yrd的权重；Xbd表示DMUd的第b个输入指标；υbd为Xbd的权重；Ea为第a个决策单元DMUa的自评效率；Yra表示第a个决策单元DMUa的第r个输出指标；μra为Yra的权重；n为决策单元的个数；Xba为第a个DMUb的第b个输入指标;νba为Xba的权重；ε为比任何正数都小的非阿基米德数。约束(19)式规定了所有DMU的效率值应介于0～1之间。约束(20)式规定了所有权重应大于0.

传统DEA模型还存在两个缺点：1)由于其采用的是自评效率，只能区别有效单元(效率值等于1)和无效单元(效率值小于1)，无法对有效单元进行排序；2)计算得到的输入和输出权重不唯一[13]。针对第1个问题，SGCES-MOEA通过计算各DMU的交叉效率，可以对所有DMU进行评估和排序。针对第2个问题，SGCES-MOEA通过构建二次目标模型，使得权重向量取值唯一。

交叉效率计算方法如下。

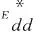
(21)

根据CCR模型对每个DMU分别求其自评效率，再根据(21)式求每个DMU的相互之间的互评效率，得到互评效率矩阵：

则DMUa的交叉效率为

(22)

由于CCR中求得的最优权重组合可能不唯一，在利用(21)式计算交叉效率时其值也不唯一。为解决此类问题，Doyle等提出了通过引入二次目标的方法，在多重最优解中选择一组最优解，以最终确定每个DMU的交叉效率[14]。常用的二次目标方法有激进型策略和慈善型策略[15]。本文的二次目标交叉效率DEA模型如下：

(23)

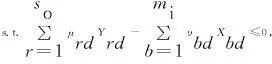
(24)

(25)

(26)

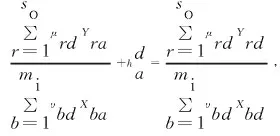
(27)

(28)

(29)

(30)

μra≥ε，r=1,2,…,so；

(31)

υba≥ε，b=1,2,…,mi.

(32)

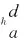
3 算例及其分析

3.1 算例描述

以某次演习任务的维修备件的支援保障为例，共有6个用装单位在前线执行演习任务。根据装备的损坏情况，通过维修任务确定需要的备件种类和数量。为检验支援保障能力，部分关重件未随部队携行，仅由后方供应。维修备件的储备由两个后方仓库承担，同时在后方仓库和用装单位之间有4个备选可开设野战仓库。备件由后方仓库运送至野战仓库，再根据前线需求由野战仓库进行分配转运至各个用装单位。后方仓库、野战仓库以及用装单位的相关数据见表1～表5.

表1 单位备件在各节点间的运输时间Tab.1 Transportation times of spare parts between nodes h

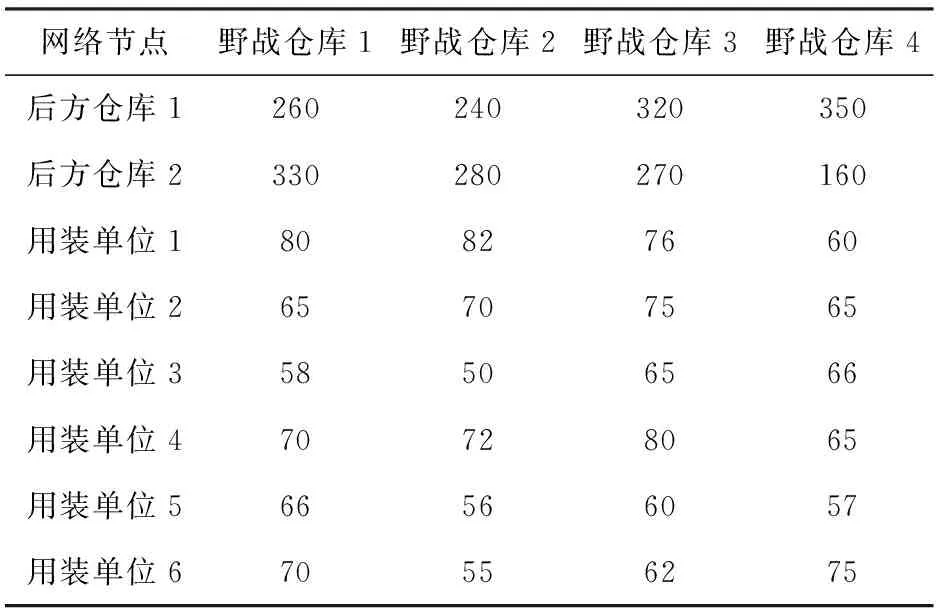
表2 单位备件在各节点间的运输成本Tab.2 Transportation costs of spare parts between nodes 元

表3 野战仓库和用装单位间路线中断风险Tab.3 Disruption risk of transit routes from fieldwarehouses to demand units

3.2 多目标优化结果

利用SGCES-MOEA对算例模型进行求解，本文采用MATLAB 2014b软件进行编程，平台为个人笔记本(Intel Core i5-6300HQ (2.3 GHz/L3) CPU和4.00 GB RAM)。相关参数设置如下：种群规模为100，外部存档规模为100，最大迭代次数为500，变异因子为0.9，交叉率为0.8，选择阈值为0.8，初始惩罚因子为10 000 000，惩罚系数为10 000.

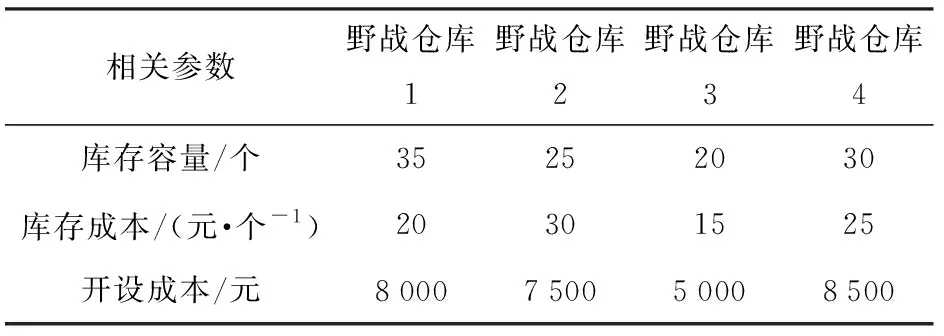
表4 野战仓库的库存容量、单位备件库存成本、开设费用Tab.4 Inventory capacity, unit spare parts inventorycost, and running cost of field warehouse

通过计算，算法共求得13个非支配解，每个解代表一个供应方案。表6给出了所有方案的输入指标、输出指标以及交叉效率和自评效率的值。其中满足度1～6为6个用装单位的备件满足度。由表6可以看出，13个方案中有10个方案为有效方案，其自评效率均为1，仅通过自评效率无法进一步从这10个方案中选出最优方案。通过计算和比较各方案的交叉效率，可以选出最优方案，其交叉效率值最大为0.927 8.

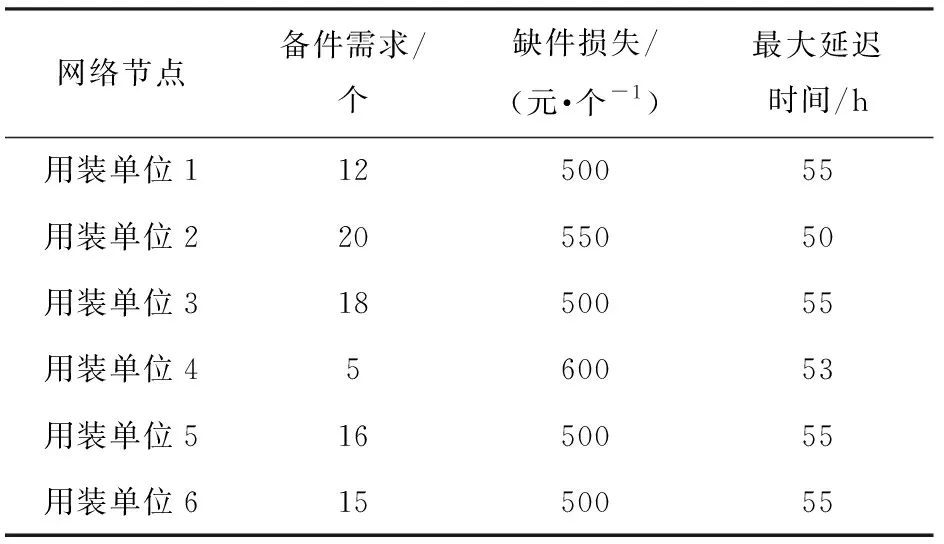
表5 用装单位的备件需求、缺件损失、最大延迟时间Tab.5 Spare parts requirements, missing loss, maximumdelay time of demand units

表6 SGCES-MOEA求解结果Tab.6 Solved results of SGCES-MOEA

3.3 灵敏度分析

通过算例的计算结果可以看出，通过SGCES-MOEA可以求得模型的非支配解并根据效率进行排序，从而选出最优解。为了进一步验证本文的排序策略对算法和结果的影响。分别用未进行排序的MOEA和采用自评效率排序的多目标进化算法(SES-MOEA)对模型进行优化，将其结果与SGCES-MOEA的结果进行比较。

表7为MOEA求得的16个非支配解的相关指标，由于未采用排序机制而没有计算自评效率和交叉效率值。16个DMU仅存在非支配关系，无法进一步决策出最优的供应方案。表8为SES-MOEA求得的7个非支配解的相关指标及其自评效率值。由表8可以看出SES-MOEA结果中有4个DMU的效率值等于1，为有效DMU，剩余3个为非有效DMU. 此时仅通过自评效率同样无法进一步选择最优供应方案。

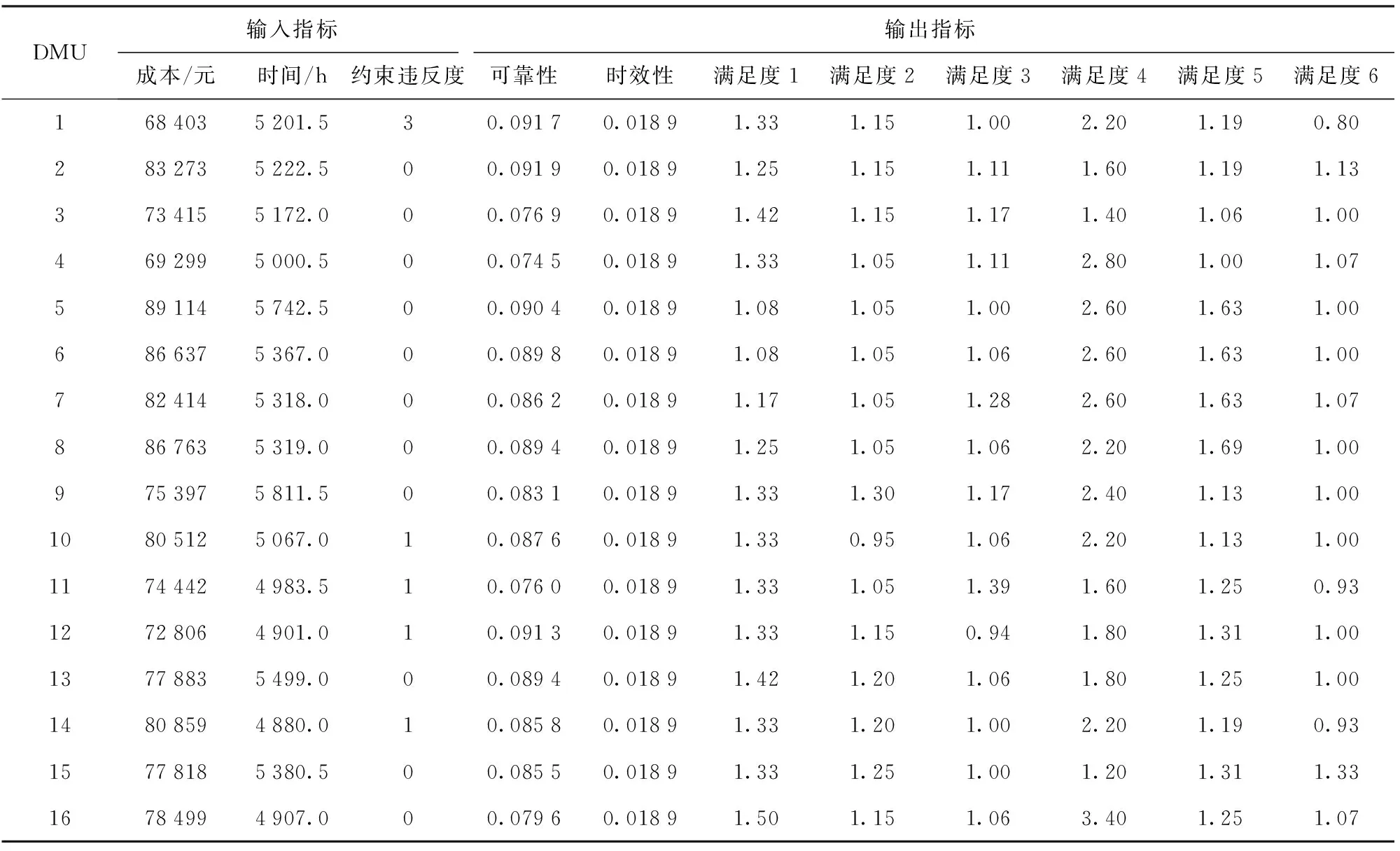
表7 MOEA求解结果Tab.7 Solved results of MOEA

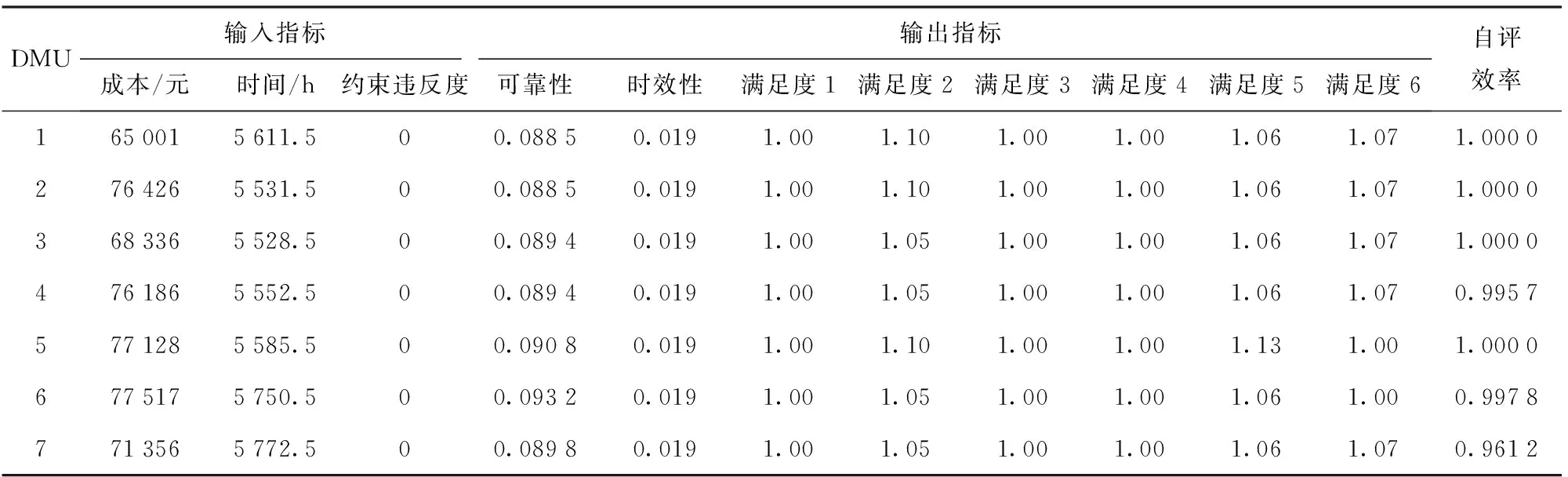
表8 SES-MOEA求解结果Tab.8 Solved results of SES-MOEA

为了验证3种算法求得方案的优劣，将SGCES-MOEA、MOEA和SES-MOEA求得的所有DMU混合后作为整体，进一步使用本文的二次目标交叉效率DEA法计算所有DMU的自评效率和交叉效率，并根据交叉效率进行排序。所有DMU的效率值如图3所示。从图3中可以看出，SGCES-MOEA对应的交叉效率值普遍较大，而MOEA对应的交叉效率值普遍较小，SES-MOEA介于二者之间。通过计算发现：SGCES-MOEA对应DMU的平均交叉效率值为0.878 5；MOEA对应DMU的平均交叉效率值为0.723 8；SES-MOEA对应DMU的平均交叉效率值为0.752 7. 由此可见，SGCES-MOEA的效果要优于其他两种算法。

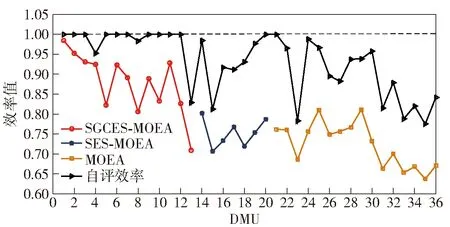
图3 3种算法结果的效率值对比Fig.3 Comparison of efficiency values of solved results of three algorithms

4 结论

本文主要解决备件供应优化决策问题，同时考虑时间、风险和成本3个目标，建立了备件供应网络优化的多目标优化模型。使用基于交叉效率排序的MOEA求得模型的非支配解集，并决策出最优供应方案。研究内容的主要贡献有：1)提出的多目标优化算法和约束处理方法可以解决备件供应的多目标约束优化问题；2)提出的基于效率排序策略可以进一步对非支配解排序，同时可以指导算法向效率最大的个体收敛；3)通过计算交叉效率克服了仅凭自评效率无法对有效单元进行排序的问题；4)提出的二次目标DEA模型解决了评估权重不唯一的问题。综上，本文的模型和算法为解决备件供应优化以及最优备件供应方案决策提供了框架和求解思路。