引入角加速度测量的柔性飞行器姿态控制方法

张博伦， 周荻

(哈尔滨工业大学 航天学院， 黑龙江 哈尔滨 150001)

收稿日期：2020-01-05

基金项目：国家自然科学基金项目(61773142)

作者简介：张博伦(1994—),男,博士研究生。E-mail: bolun1104@163.com

通信作者：周荻(1969—)，男，教授，博士生导师。E-mail：zhoud@hit.edu.cn

0 引言

导弹等飞行器为了能够顺利地飞向目标，要求目标始终处在飞行器导引头的视场之内。这就需要飞行器的俯仰角ϑ和偏航角ψ分别跟踪视线倾角qε及视线偏角qβ. 现有针对刚体飞行器的姿态控制方法[1-3]并不能实现对于柔性飞行器姿态的跟踪控制。已发表的针对柔性飞行器的姿态控制方法，通常将弹性振动的影响视为模型不确定性或外部扰动，引入干扰观测器对弹性振动引起的扰动进行观测[4-6]，在设计控制律时对弹性扰动进行补偿。Shahravi等[7-8]和Jin等[9]直接设计具有鲁棒性的控制器，对柔性飞行器进行了姿态控制。Gennaro[10]和Zhu等[11]在设计控制律时，没有使用角速度测量信息便可实现对姿态角的控制。此外，使用文献[11]中的方法能同时使得弹性振动最终收敛至0，但是需要在没有外界扰动的情况下才能实现。Hou等[12]提出了一种无模型自适应控制的方法，Qi等[13]将其应用到对柔性飞行器的姿态控制。在角速度测量信息没有受到柔性影响的情况下控制效果理想，但是当测量信息由于弹性振动而不准确时，姿态角也会在指令值附近大幅震荡。此外还有在柔性附件上安装压电器件的方法[14-15]，通过调节输入电压抑制相应柔性附件的振动。以上方法的共同特点是都需要使用刚体姿态角、角速度等信息，并认为其是准确可测的。在工程实际中，对于细长型柔性飞行器(特别是导弹)，弹体整体都会受到柔性振动的影响。受惯性导航(以下简称惯导)系统安装位置的影响，角速度的测量会附加对应位置柔性形变，即不能获取刚体真实的姿态角及角速度信息。若直接将带有柔性影响测得的姿态角、角速度等信息代入所设计的控制律，会使计算得到的控制力矩与真实需要的控制力矩不相符合。若简单地将弹性振动产生的影响视作模型的不确定性和外部扰动，在测量信息有误差的情况下使用上述控制方法，极易使得姿态控制系统发散。

根据对柔性飞行器的研究[16]及有限元建模方法的使用[17]，柔性特性可简化为一个2阶振荡环节，柔性形变程度与飞行器所受转动力矩有关。Oh等[18]和Zhou等[19]使用陷波滤波器对角速度的测量进行了滤波估计；杨永泰等[20]通过采用前馈的控制方法抑制弹性振动，在没有外部扰动力矩的情况下，能很好地对刚体的角速度进行估计或弹性振动进行抑制；但是当存在外部扰动时，对刚体角速度的估计及弹性振动抑制效果将不再理想。角加速度计的应用[21-22]，使获取角加速度从而间接获得作用在飞行器各轴方向的控制与扰动总力矩成为了可能。

针对扰动环境下刚体飞行器姿态控制有很好效果的传统滑模控制方法，由于切换项的存在，不仅会导致抖震，而且控制力矩的突变还会激发柔性形变。受此启发，对于柔性飞行器的姿态控制系统，采用的控制器应该避免过大的增益；在实现姿态指令跟踪的过程中，逐步降低飞行器柔性变形程度也是必要的。

本文主要研究在姿态角及角速度有弹性振动产生的测量误差情况下大气层外飞行器的姿态控制问题，以保证目标始终处于导引头视场之内。 引入角加速度计的测量，间接得到作用在飞行器上的力矩。结合弹性振动特性，对刚体真实的角速度信息进行估计。同时也将并不精确验前已知的弹性振动频率当作一个状态量进行实时在线估计，验证了整个滤波估计系统的可观性。此外，针对未来细长型飞行器的特点，为了减小弹性振动对惯性器件测量的影响，使姿态控制发动机具备提供连续推力的能力，使用了动态面的方法进行姿态控制律的设计。

本文内容的结构如下：第2节建立了大气层外飞行器柔性振动模型和飞行器在刚体部分绕质心转动的运动学、动力学模型，分析了柔性形变对惯导系统及角加速度计测量的影响；第3节设计了姿态角指令跟踪控制器，使用动态面控制方法，使姿态角跟踪误差半全局稳定，具有一定鲁棒性；第4节研究了角加速度及角速度的滤波器设计，在测量器件受到柔性影响下，通过设计相应的滤波器分别估计了刚体部分的角加速度及角速度；第5节针对具体问题进行了仿真验证；第6节对柔性飞行器的姿态控制问题进行了总结。

1 建立柔性飞行器相关模型

1.1 柔性特性

根据假设模态法可以将柔性振动写为

(1)

在实际情况中，飞行器的滚转方向受柔性影响很小，可忽略不计。因此本文只考虑柔性变形对俯仰及偏航方向的影响。此外，1阶模态对于柔性形变起主导作用，在后续分析中只考虑1阶模态。对于大气层外飞行器，没有气动特性对柔性形变的影响，广义坐标q1(t)的动态模型可用一个2阶振荡环节表示为

(2)

1.2 飞行器刚体部分姿态动力学及运动学模型

刚体部分姿态动力学模型可表示成如下形式：

(3)

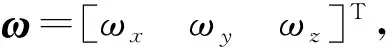
选择俯仰角ϑ→滚转角γ→偏航角ψ(z轴→x轴→y轴)坐标轴转换的顺序，空间飞行器刚体部分的姿态运动学方程用四元数可以表示为

(4)

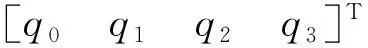
(5)

1.3 惯导系统及角加速度计测量模型

在柔性和测量噪声的影响下，将飞行器长度做归一化处理，惯导系统对角速度的测量方程为

(6)

式中：ωxm、ωym、ωzm表示对飞行器角速度的测量值；μy、μz为惯导系统安装位置处对应模态的振型函数；v1,x、v2,y、v3,z为惯导系统对角速度的测量误差。类似地，可以得到角加速度计测量方程为

(7)

式中：aωxm、aωzm、aωzm表示对飞行器角加速度的测量值；μ′y、μ′z为角加速度计安装位置处对应模态的振型函数；ν4,x、ν5,y、ν6,z为角加速度计对3个轴向的角加速度的测量误差；aωx、aωy、aωz为飞行器刚体部分真实的角加速度，

(8)

控制的目标是：在测量hω、ha受到柔性影响的情况下，控制刚体的姿态角ϑ、ψ、γ，以跟踪指定指令。

2 动态面姿态控制方法设计

(9)

式中：

柔性空间飞行器总的姿态跟踪系统可描述为

(10)

取z2=x2-α(z1,xd)，α(z1,xd)定义在下文给出。用动态面控制技术设计,定义虚拟控制为

(11)

(12)

(13)

于是，姿态跟踪系统可表示为

(14)

对于具有有限初始状态的闭环系统(14)式，设计如下控制律：

(15)

式中：P2为一个正定对角矩阵。

3 估计刚体角速度及角加速度的滤波器设计

第2节根据(15)式设计的姿态控制律是与刚体状态有关的状态反馈，控制目标为刚体的姿态角。但是惯导系统测量所得到的角速度信息受到了柔性的影响。若直接将测量值用于控制律，会使控制系统不能正常工作，姿态角趋于发散。因此需要设计滤波器估计刚体的角速度，并通过对估计的角速度积分获得刚体姿态角的估计值。

3.1 引入角加速度测量并对其进行滤波估计

若只根据惯导系统测量的角速度信息设计滤波器，将会遇到很大困难。这是因为轨控发动机质心偏移等因素产生的干扰力矩F只能当作模型误差处理。在实际情况中，轨控发动机推力大小由制导律计算得到，是时变的，其对姿控系统产生的干扰力矩难以用数学规律描述，若将其当作模型误差处理，会对角速度的估计产生不利影响。

在此情况下，观察(2)式柔性震荡的特性，若能获取姿控发动机产生的控制力矩u和干扰力矩F，在阻尼矩阵C1、刚度矩阵K1以及增益矩阵D已知的情况下，可较为精确地得出飞行器柔性形变的数值。此外，由(3)式可得，若控制力矩u和干扰力矩F已知，在对刚体角速度进行滤波估计时，便可将二者作为已知输入而非模型误差进行处理，在此情况下，对刚体角速度的估计效果将明显提升。

考虑到获取控制力矩u和干扰力矩F的必要性，选择引入角加速度计的测量通过(8)式间接获得总力矩。由(7)式注意到角加速度计测量是受到柔性影响的，若不经过处理直接使用，将会使总力矩的估计值与真实值产生较大误差。为了获得较为精确的角加速度，本文使用陷波滤波器对角加速度测量值进行滤波。

由于x轴方向的角加速度计测量没有挠性影响，故将测量值直接作为估计值，即

ωx=aωxm.

(16)

以y轴方向为例介绍陷波滤波器，

ωy=G(s)aωym，

(17)

式中：

ω1=2π(f1-3),f1是弹性干扰信号的标称频率，f1=ωny/(2π)，在该滤波器中将它设置为中心频率；ω2=2π(f1-1)；ω3=2π(f1+1)；ω4=2π(f1+3)。同理，可获得绕z轴转动的角加速度估计值ωz.

3.2 使用推广卡尔曼滤波器估计刚体角速度

对于轴对称飞行器，通常y轴和z轴方向的振荡频率与阻尼是相同的。在实际情况中，飞行器真实的柔性振荡频率会在ωny、ωnz测定基础上有所变化，不能精确地验前已知。在建立角速度滤波估计模型时，将柔性振荡频率ωn也作为一个状态变量，其动态过程视为一个慢时变的随机游走。使用角加速度的估计值ωx、ωy、ωz作为系统输入，结合(2)式和(3)式，可以建立角速度与柔性形变的系统模型。

选取系统状态变量为

状态方程写作向量方程的形式为

(18)

ν7为高斯白噪声，以此代表一个慢时变的随机游走过程。测量函数写作

(19)

根据非线性系统可观性理论[23-24]可以判断系统(18)式和(19)式是可观的(具体过程如下)。系统方程(18)式阶次为n=8，对测量(19)式求直到n-1=7阶的Lie导数：

依此类推, 进一步可求得

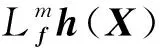
则系统观测矩阵为

(20)

计算结果表明(20)式中矩阵O的秩等于8，即等于系统状态的维数，那么根据非线性局部弱可观性理论，可以判定该系统完全能观。

应用推广卡尔曼滤波器理论，可以得到状态X的估计值. 其中状态估计量x、y、z进行积分，可以得到对刚体姿态角的估计值、、，通过(5)式得到姿态四元数。角速度的估计值及姿态四元数的估计值代入控制律(15)式，可以实现较好的姿态跟踪效果。具体仿真结果将在第4节体现。

4 仿真结果

在仿真实例中，柔性飞行器相关参数取为：Jx=0.125，Jy=Jz=0.32，ξy=ξz=0.001 3，dy=dz=2.2，μy=μz=1，μ′y=μ′z=-1.2；测量噪声ν1,x、ν2,y、ν3,z为0均值、标准差为3×10-3的高斯白噪声，ν4,x、ν5,y、ν6,z为0均值、标准差为0.175的高斯白噪声。姿态角跟踪指令为xd，由ϑd=qε、ψd=qβ、代入(5)式求得，其中qε、qβ是导引头计算出来的视线角。此外，弹性振动频率在标称值ωn/(2π)=44 Hz的基础上有±3 Hz范围内的随机扰动。扰动力矩是飞行器的轨控发动机在实现制导指令时产生的干扰力矩，其数值大小如图1所示。

图1 干扰力矩Fig.1 Disturbance torque

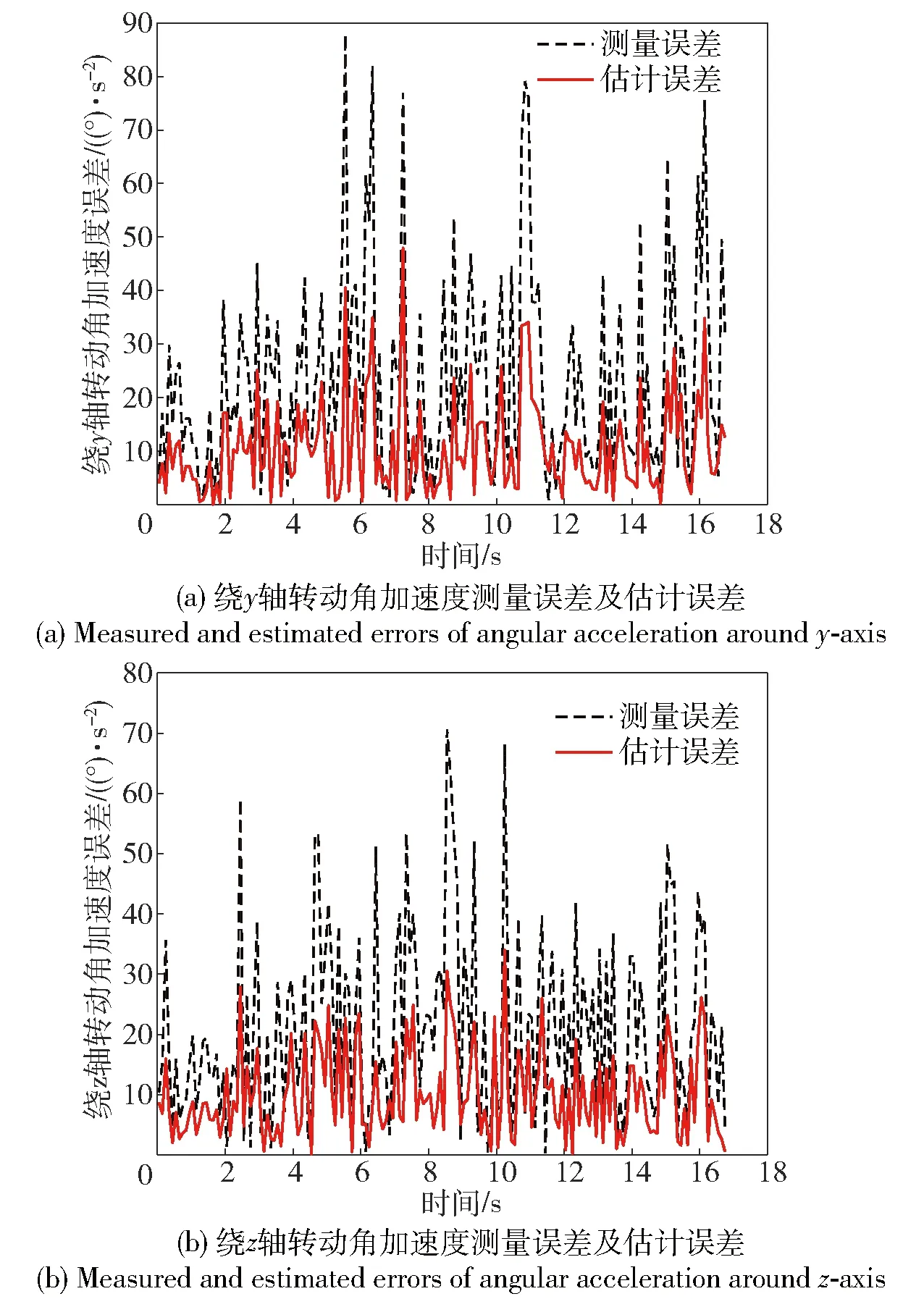
图2 角加速度误差Fig.2 Errors of angular acceleration

经过陷波滤波器处理后的角加速度估计误差与角加速度计测量误差如图2所示。从图2中可以看出，陷波滤波器在没有外界其他扰动的情况下，对排除柔性干扰有较好的作用。对弹性振动的估计效果如图3所示，对振动频率的估计如图4所示，产生误差(见图4)的原因是(18)式中角加速度引入的误差并不是高斯白噪声，使用卡尔曼滤波器处理这种噪声有一定难度。角速度估计效果如图5所示，姿态角跟踪效果如图6所示。

图3 弹性振动参数的估计值与真实值Fig.3 Estimated and true values of elastic vibration parameters

图4 振动频率Fig.4 Vibration frequency

图5 角速度估计值与真实值Fig.5 Estimated and true values of angular velocity

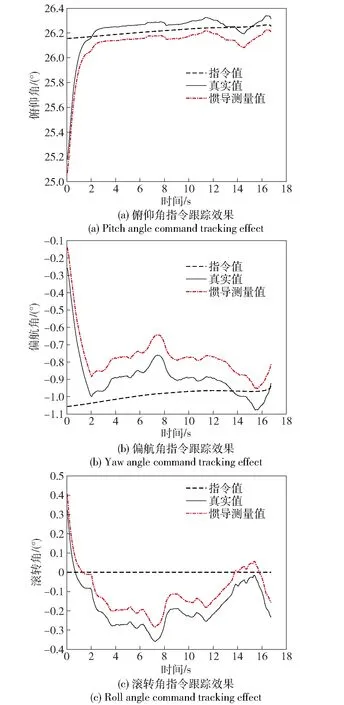
图6 姿态角Fig.6 Attitude angles

为了体现测量误差对姿态控制系统的影响，将惯导系统测量得到的角速度和姿态角信息直接代入控制律(15)式。得到姿态角跟踪效果如图7所示。惯导系统对y轴、z轴方向角速度测量值与真实值对比如图8所示。

由图8可以看出，惯导系统对角速度的测量误差是发散的。这是因为带有柔性误差的测量值代入控制律(14)式将不能产生期望的控制力矩，而期望力矩与实际输入力矩的偏差又会激发出更大的弹性形变，产生更大的测量误差。当姿态角跟踪误差的大小超出导引头视场大小后，飞行器将失控。

文献[13]中所提无模型自适应控制方法，通过规避给控制系统建模来解决柔性振动带来的不确定性。该控制方法对于测量器件同样受到柔性影响的姿态控制效果如图9所示。在使用该控制方法时，姿态角的测量值也是经过滤波器处理之后再进入控制系统的，尽管如此，姿态角仍在指令附近有较大的波动。由此可以看出柔性振动对惯导系统测量的作用将会对控制系统产生非常不利的影响。

图7 姿态角(使用角速度测量值)Fig.7 Attitude angles(using the measurements of angular velocity)

图8 角速度估计值与真实值Fig.8 Estimated and true values of angular velocity

图9 姿态角(使用无模型自适应控制)Fig.9 Attitude angles(using model-free adaptive control)

结合图1可知，受到制导指令的影响，飞行器轨控发动机产生的干扰力矩是不可避免的。受此影响，在实际情况中难以将弹性振动完全抑制，只能选取合适的控制增益，在满足姿态指令跟踪精度的基础上尽量减少作用在飞行器上的总力矩，使柔性形变处在合理的区间内。

5 结论

针对测量器件受到飞行器柔性影响的问题，本文通过滤波器设计估计出了弹性振动的形变程度以及弹性振动频率，获得了刚体姿态角及角速度的估计值。将上述刚体状态的估计值代入所设计的控制律，虽然没有使姿态角跟踪误差收敛至0°，但是保证了误差小于0.5°. 对于制导问题，该精度可以保证目标始终处于导引头视场范围(通常为2°)之内。