基于频率域三维等效源的磁梯度张量转化方法
2021-01-08李金朋范红波张英堂李志宁尹刚孙富成
李金朋, 范红波, 张英堂, 李志宁, 尹刚, 孙富成
(1.陆军工程大学石家庄校区 车辆与电气工程系, 河北 石家庄 050003;2.中国空气动力研究与发展中心 高速空气动力研究所,四川 绵阳 621000; 3.63880部队, 河南 洛阳 471003)
0 引言
随着磁异常检测理论的不断进步和发展,磁梯度张量数据因为具有高分辨率的特点而逐渐成为当前的研究热点[1-2]。地磁背景场的磁梯度较低,张量分量主要反映近地磁源的梯度数据,因此利用磁梯度张量分量数据能够实现磁源定位、二维边界识别、深度反演以及三维姿态反演等计算[2-4],并广泛应用于军事侦察(未爆弹、潜艇和水雷等)和民用等领域。
等效源计算方法能够利用等效源模型对磁源的观测数据进行重建,是一种应用广泛的数据处理方法。在传统的等效源计算方法中,常常利用空间域的等效源计算方法构造地下单层或多层等效源模型。Lyrio[5]利用等效源的计算方法对不规则数据进行插值计算;Ali等[6]利用三维等效源计算方法,实现对观测数据进行延拓计算;陈涛等[7]基于三维等效源法对重力数据进行等效源模拟,获得重力梯度张量数据。在三维等效源计算方法中,在利用多层等效源进行计算时,计算精度会提高,模拟场源与真实场更加接近,但计算过程类似于三维反演,提高了计算难度和计算成本,在处理大规模数据的过程中受到一定的限制。李端等[8]提出多层等效源的计算方法,并应用于磁源的磁测数据转换,但是如何确定多层等效源的参数设置,需要进一步的探索。谢汝宽等[9]提出利用最小拟合差的单层等效源计算方法,该算法计算速度快,能够直接对磁源的深度进行估计。
频率域的计算方法具有简单、快速的计算特点。Mickus等[10]基于快速傅里叶计算原理将重力垂直分量转化为重力梯度张量;Jiang等[11]提出了利用余弦变换的方法对重力梯度张量数据进行计算。上述频率域的计算方法计算速度快,但是受噪声影响较为明显。
本文针对上述问题,提出基于频率域三维等效源的磁梯度张量转换方法。首先,提出频率域条件下的磁梯度张量正演计算方法;然后,构建频率域三维等效源模型,并利用迭代法进行计算,以提高计算精度。最后,将获得的地下等效源模型的磁化强度通过C范数正则化选择方法进行正演计算,以提高计算结果的稳定性。
1 方法原理
1.1 频率域正演基本理论与方程
假设观测面为平面,将地下划分为不同深度的水平长方体层,设置长方体层具有相同的尺寸大小。在地理坐标系下,x轴正方向指向北向,y轴正方向指向东向,z轴正方向指向垂直向下。观测面高度设置为zs(m). 假设某一长方体平面的顶面深度为zh(m),底面深度为zb(m). 长方体层的磁异常Bz分量与磁化强度M分布的频率域计算公式[12]为
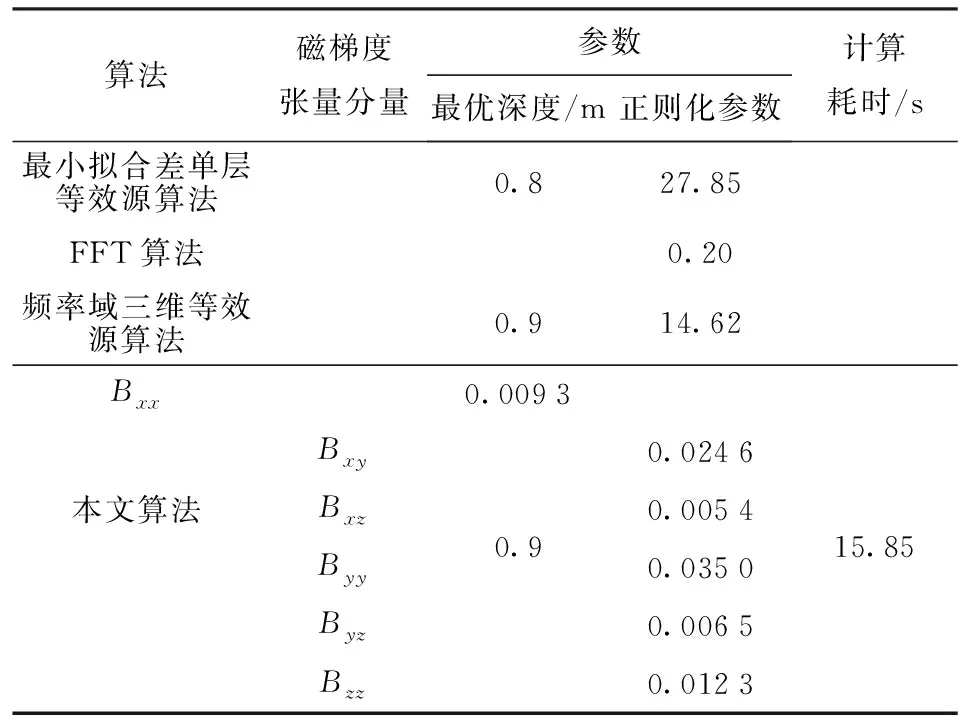
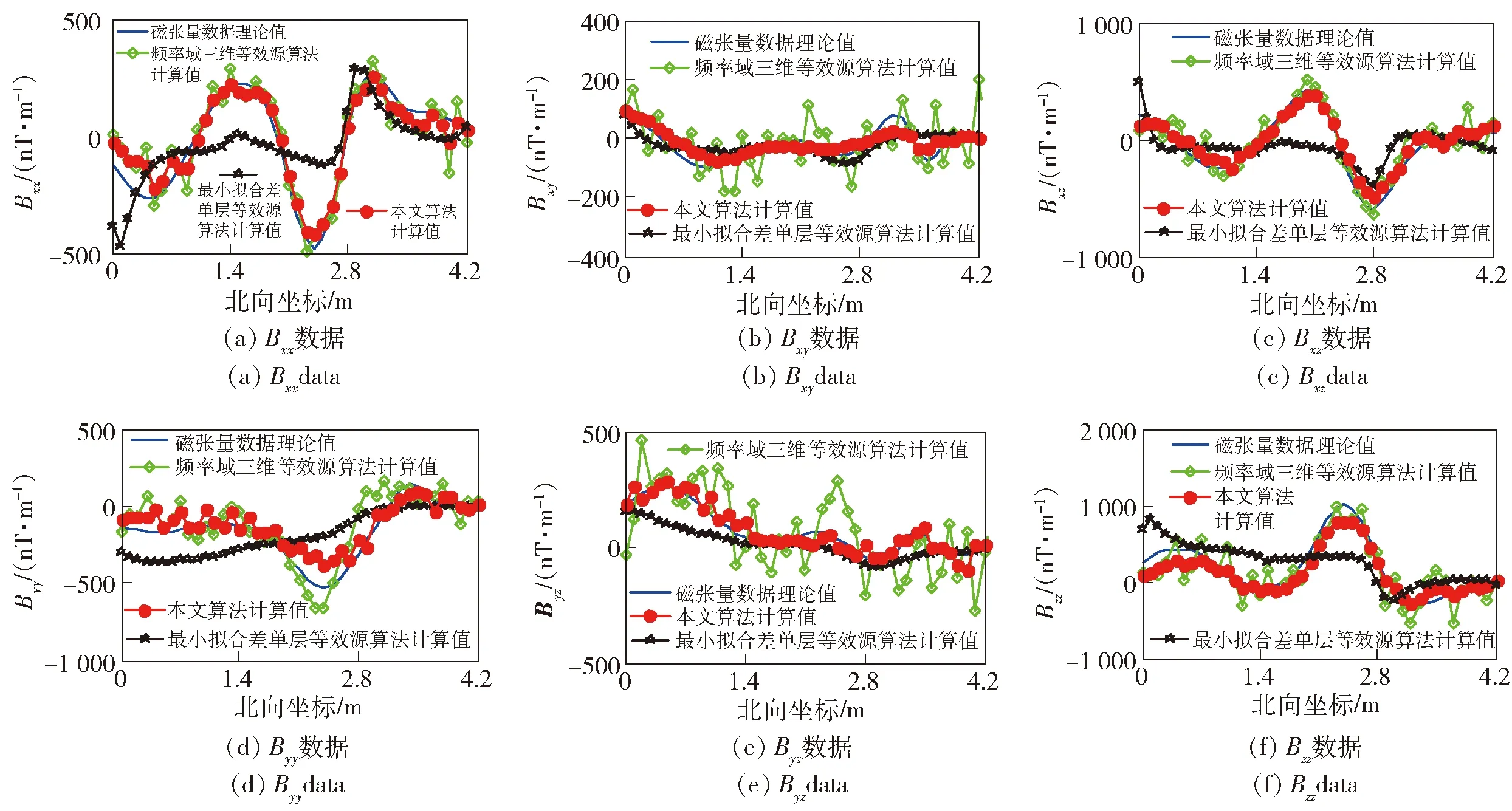
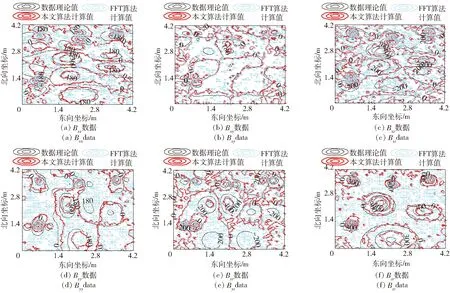
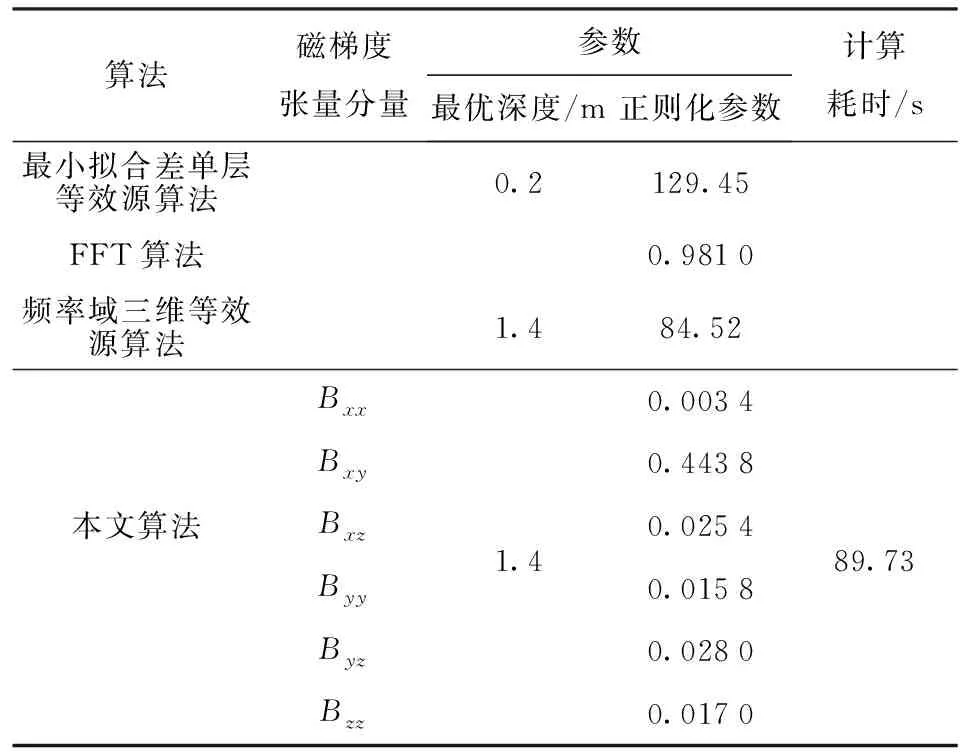
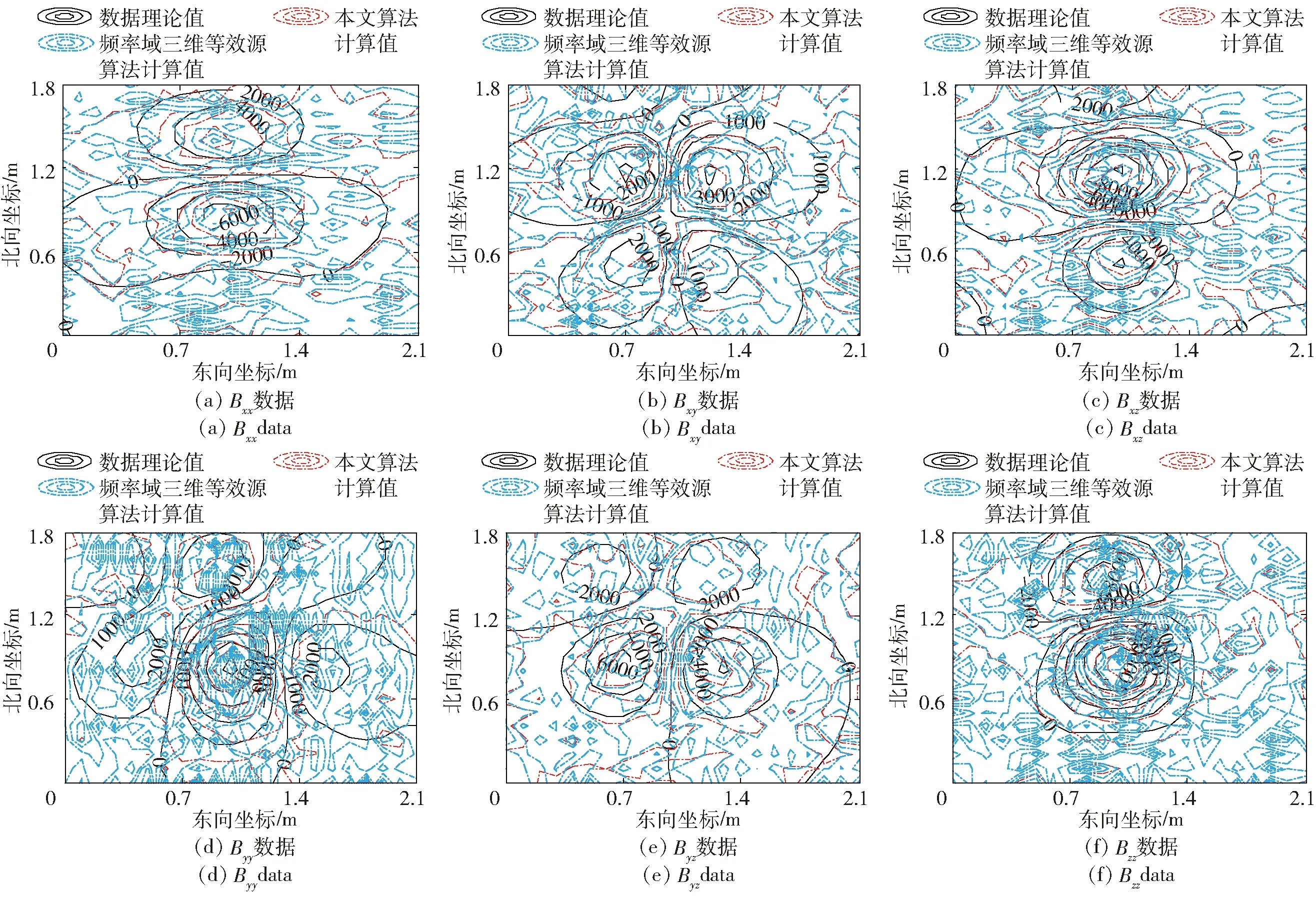
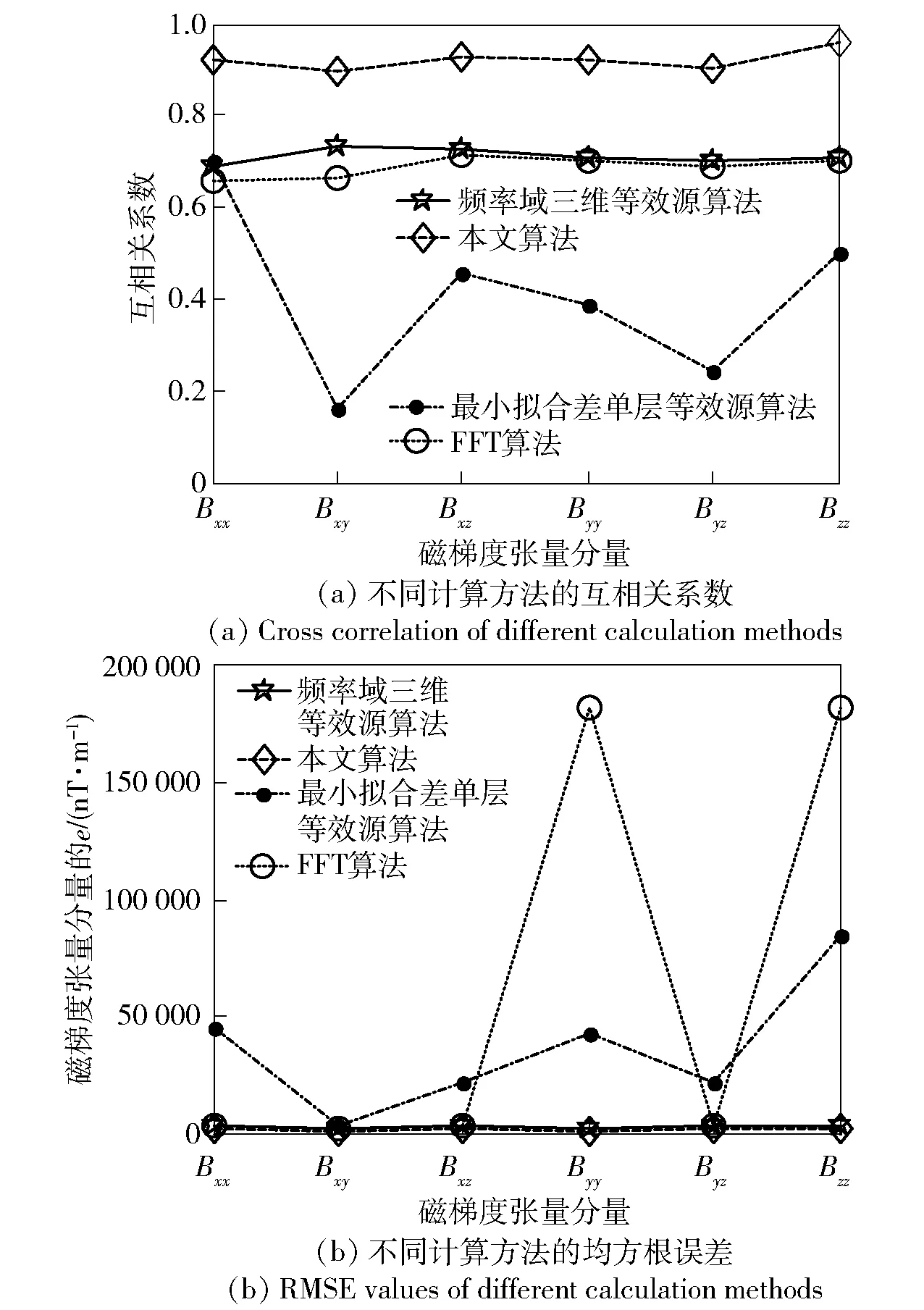
F[Bz]={2πCmΘme|k|zs(e-|k|zh-e-|k|zb)}· (1) 式中:F[]为对数据进行二维傅里叶变换;Cm=μ0/(4π)为常量,μ0为磁导率,μ0=4π×10-7H/m;Θm=(i·(xkx+yky)+z|k|)/|k|,x、y、z分别为实际磁化方向与x轴、y轴、z轴方向夹角的方向余弦,kx和ky分别为沿x轴、y轴方向的角频率, 假设U是磁势异常,则观测面上的磁异常场总强度矢量ΔT[13]可以表示为 (2) (3) 利用二维傅里叶变换以及傅里叶变换的空间域微分定理,可以得到磁总场异常与三分量之间的频率域转化关系[13]为 (4) 磁梯度张量是磁场矢量B=[Bx,By,Bz]沿着x轴、y轴、z轴3个正交方向上的空间变化率。则磁梯张量矩阵G可以写成分别包含3个矢量元素的两个矩阵的乘积: (5) 式中:Bab(a,b=x,y,z)为磁梯度张量分量数据。对(5)式进行二维傅里叶变换,得到 (6) 根据(4)式和(6)式,可以得到傅里叶变换后的磁梯度张量全张量数据: F[G]=ξ·F[Bz], (7) 假设观测面为平面,磁场H与磁源之间的关系[14]可以表示为 (8) 式中:R代表积分函数在三维空间内定义;L=[(xV-xO)2+(yV-yO)2+(zV-zO)2],(xO,yO,zO)为观测点坐标,(xV,yV,zV)为三维空间中体积元dv的坐标。 由于将待测区域划分为无数长方体层,磁化分布仅在x轴和y轴方向上变化,因此将(8)式转化为两个部分:沿东- 北方向的水平部分S,以及沿z轴方向的垂直部分U[15],二者的关系为 (9) (9)式的频率域计算公式[15]为 (10) 因此,磁异常Bz分量的频率域计算公式[15]可以表示为 (11) 根据(11)式计算得到第c(c=1,2,3,…,Q,Q为划分层数)层地下水平层的磁化强度Mc分布[16]为 (12) 式中:h(kx,ky,zc)=(zce-|k|zc)s,s为常数。 根据(2)式,可以获得不同水平层的磁化强度分布Mc. 根据获得磁源的三维磁化强度分布,利用(7)式以及(11)式能够得到磁源的磁梯度张量数据。 在对磁梯度张量数据进行转化过程中,观测面的磁异常分量Bz数据中常常存在噪声。由于张量转换系数ξ的噪声放大特性,导致获得的张量数据计算结果不稳定。为了抑制高频噪声,将正则化参数引入计算方程,构造一个极小化正则化泛函[17-18]: min{‖ξ-1·F[G]-F[Bz]‖2+λ‖F[G]‖2}, (13) 式中:λ为正则化参数。上述极小化问题的解为 F[G]=Aξ·F[Bz], (14) 在上述计算过程中,对正则化参数的选择十分重要,数值过小将没有滤波效果,数值较大将使计算的张量数据不准确。本文采用C范数的计算方法对正则化参数进行选择[19],计算不同正则化参数下相邻两个结果之间的C范数值,确定局部极小值对应的正则化参数为最优正则化参数。因此,通过选择最佳的正则化参数,可以获得稳定且准确的磁梯度张量数据。 为了进一步提高三维频率域等效源计算方法的精度,本文利用迭代法确定磁源的各项参数。 步骤1对观测面上的磁异常Bz分量进行二维傅里叶变换。 步骤2利用(12)式依次计算每个水平层的二维磁化强度分布的频谱数据,得到三维磁化强度分布数据Mc。 步骤3利用正演计算(1)式计算得到磁异常Bz,n分量,并计算观测数据Bz与计算数据Bz,n的差值B′z,n,n表示第n次迭代计算,n=1,2,…,N,N为最大迭代次数。 步骤4计算B′z,n的均方根误差,当均方根误差大于容差极限且迭代次数未达到最大迭代次数时,计算B′z,n数据的磁化强度三维反演结果M′c,对磁化强度进行更新Mc+1=Mc+M′c,重复计算,直到均方根误差小于容差极限,或者迭代次数达到最大迭代次数。 利用频率域三维等效源方法对磁梯度张量数据进行计算,需要确定地下划分的网格数量及尺寸,由于频率域计算速度快,因此采用与观测点相同的划分方式对地下网格的水平方向进行划分,在垂直面的分布深度上,利用迭代法思想设置不同的深度,对磁测数据反演精度进行计算,将达到精度要求对应的深度,作为地下三维网格的垂直深度。 为了对本文方法进行有效分析,构建7个不同模型对本文方法进行验证。将水平观测面划分为43×43=1 849个网格,网格间距为0.1 m. 模型的地下正演模型分布如图1所示,各模型具有不同的形状、位置、磁化方向以及磁化强度,具体物性参数如表1所示。地磁背景场的磁化方向为磁倾角I为60°,磁偏角D为20°. 图2为组合模型在观测面上的磁异常Bz分量数据,图2(a)为模型理论磁异常Bz分量,图2(b)为加入信噪比为20 dB的高斯噪声的磁异常Bz分量,其中虚线为观测线,观测线上不同模型磁异常Bz分量数据见图2(c)所示,模型的理论磁梯度张量数据如图3所示。 图1 地下正演模型Fig.1 Underground forward model 表1 模型理论物性参数Tab.1 Physical and geometrical properties of models 图2 模型产生的磁异常Bz分量数据Fig.2 Magnetic anomaly Bz components generated by the models 图3 磁梯度张量理论数据Fig.3 Theoretical data of magnetic gradient tensor 图4 磁梯度张量与Bz分量在不同迭代次数 下的均方根误差Fig.4 RMSE values of magnetic gradient tensor and component Bz under different iteration times 确定最小拟合差单层等效源方法最佳深度时,设置地下网格最大深度为1 m,计算间隔为0.1 m. 利用图2(b)测线上的磁异常Bz分量数据进行计算,根据图像可知,该测线上的磁测数据主要由模型6和模型7的磁场组成,而模型1、模型2、模型3、模型4、模型5磁异常数几乎为0,进而可以讨论包含两种不同深度条件下组合模型不同计算方法的计算准确度。在进行等效源计算时,将地磁背景场的磁化方向作为等效源的磁化方向,不同方法得到的磁梯度张量分量数据如图5所示。根据图5可以看出,利用最小拟合差单层等效源方法计算得到的磁梯度张量数据的误差较为明显,频率域三维等效源方法与本文算法获得的计算结果与理论计算结果基本保持一致,但频率域三维等效源计算方法获得的计算结果受噪声影响较为明显,存在一定的波动。为了进一步对本文方法的抗噪性能进行说明,将本文方法以及频率域三维等效源方法获得的磁梯度张量计算轮廓进行比较,计算结果如图6所示。由图6可以看出,本文算法通过正则化计算,获得的计算结果与理论磁梯度张量较为匹配。 图5 测线上不同计算方法的磁梯度张量Fig.5 Magnetic gradient tensors of different calculation methods over the observation line 图6 磁梯度张量数据轮廓(单位:nT/m)Fig.6 Contours of magnetic gradient tensor data (unit: nT/m) 图7 磁梯度张量分量的互相关系数与均方根误差Fig.7 Cross-correlation coefficients and RMSE values of magnetic gradient tensor components 表2 仿真计算中不同算法得到的参数及计算耗时Tab.2 Parameters and time consumptions obtained bydifferent methods in simulation calculation 图8 测量装置及实测磁异常Bz分量数据Fig.8 Measurement device and measured magnetic anomaly component Bz 对地下未爆弹进行一组实测试验。试验地点位于石家庄某地,将水平观测面划分为19×22=418个网格,网格间距为0.1 m. 地磁背景场的磁化方向为磁倾角I为56°,磁偏角D为-18°. 试验所用设备如图8(a)所示,利用英国Bartington公司三轴磁通门传感器搭建十字型磁梯度张量探头,测试系统主要包括十字型探头和数字采集模块及软件操作终端。试验过程中探头固定在无磁试验台架上,利用单点测量方式,滑动张量探头在无磁滑杆上对待测区域的每一个观测点进行测量,无磁试验台架的4个固定点位置为可调整角度的三脚架结构,利用水平仪将无磁试验台架调整在同一水平面上,保证探头在测试过程中能够保持水平。十字型探头的基线距离为40 cm,在进行实际测量试验时,将单传感器测量得到的Bz数据与背景磁场的Bz数据进行做差,作为测区内该点的磁异常Bz数据,测区内实际测量数据如图8(b)所示。同时,该点的张量数据利用差分原理可以直接求解,实际测量得到的磁梯度张量分量数据如图9所示。为了减少传感器探头的噪声、不一致性、零漂以及非对准误差对测试数据精度带来的影响,该系统利用非线性校正方法进行了非线性校正[20],因此将获得的观测数据作为实测试验的理论数据。 图9 磁梯度张量实测数据Fig.9 Measured magnetic gradient tensor data 为了证明本文算法的有效性,向实测磁异常Bz分量数据中加入信噪比为40 dB的高斯噪声,获得的测量数据如图8(c)所示。通过迭代计算获得最大划分深度为8层,在最大划分层数下的迭代次数共16次。在迭代终止前,随迭代次数增加获得的张量和磁异常Bz分量的均方根误差计算结果如图10所示,测线上不同方法的磁梯度张量分量数据如图11所示,本文算法以及频率域三维等效源计算方法获得的磁梯度张量计算轮廓如图12所示。在试验计算中将实测磁梯度张量数据作为实测数据,根据计算结果可以看出,本文算法获得的计算结果能够有效降低噪声的干扰,与实测数据基本保持一致,计算效果最好。 图10 磁梯度张量与Bz分量在不同迭代 次数下的均方根误差Fig.10 The e values of magnetic gradient tensor and component Bz under different iteration times 本文算法与频率域三维等效源算法、最小拟合差单层等效源算法以及FFT计算方法进行比较,磁梯度张量分量的互相关系数与均方根误差如图13所示。由图13可见:在噪声等因素影响下,FFT计算方法受噪声影响较为明显;最小拟合差单层等效源算法计算得到的磁梯度张量数据相关性较差;本文算法的计算精度最高,通过正则化计算能够获得与实测磁梯度张量较为匹配的计算结果;FFT计算方法受噪声影响计算精度较差,与数值仿真结论相一致;在进行单层等效源计算时,需要已知先验信息,且计算结果存在一定的漏磁现象。上述方法在计算过程得到的参数以及计算耗时如表3所示。由表3可见,最终耗时结果与数值仿真结果类似,而基于最优拟合差的单层等效源算法用时最多,本文算法的计算时间居中,FFT算法耗时最短。通过上述分析可知,本文算法能够有效对未爆弹的张量数据进行计算,为下一步的定位与识别[4]提供有效的数据支持。 图11 测线上不同计算方法的磁梯度张量Fig.11 Magnetic gradient tensors for different calculation methods over the observation line 图12 磁梯度张量数据轮廓(单位:nT/m)Fig.12 Contours of magnetic gradient tensor data (unit: nT/m) 图13 磁梯度张量分量的互相关系数与均方根误差Fig.13 Cross correlation and RMSE values of magnetic gradient tensor components 对磁性异常体进行正演计算时,当噪声较大时会对张量计算结果产生一定的影响。针对上述问题,本文提出了基于频率域三维等效源的磁梯度张量正演理论,构建频率域三维等效源并利用迭代法自适应的计算网格划分深度与精度,通过C范数正则化选择方法对地下等效源模型的磁梯度张量数据进行正演计算。通过仿真和试验证明了本文方法具有如下优势: 表3 试验计算中不同算法得到的参数及计算耗时Tab.3 Parameters and time consumptions obtained by differentmethods in simulation calculation 1) 构建基于磁异常Bz分量数据的频率域三维等效源计算模型,提高了计算结果的稳定性,并减少了计算成本。 2) 利用迭代法对地下水平层深度以及磁化强度反演结果进行自适应求解计算,实现了计算过程的自动化计算。 3) 提出了基于C范数正则化计算方法的磁梯度张量正演计算方法,能够在噪声干扰下稳定的获得磁梯度张量转换结果。 磁性异常体磁梯度张量数据的正演是对磁性异常体进行数据解释的基础,通过仿真和试验证明了本文方法能够在噪声条件下实现对磁性异常体的张量数据正演,为未爆弹药等隐蔽武器的探测与数据解释提供了有力的技术手段。
F[M],zs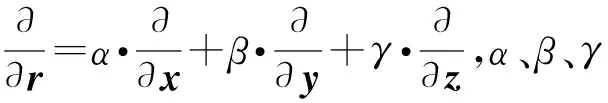
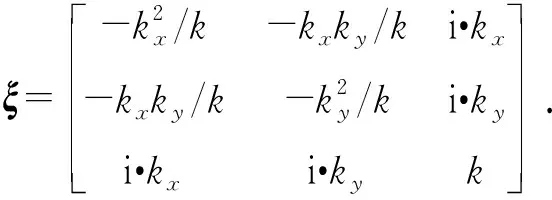
1.2 频率域三维等效源模型
1.3 磁梯度张量数据正则化转化理论
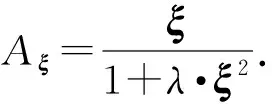
1.4 迭代计算法
2 数值仿真
2.1 正演模型及本文参数选择
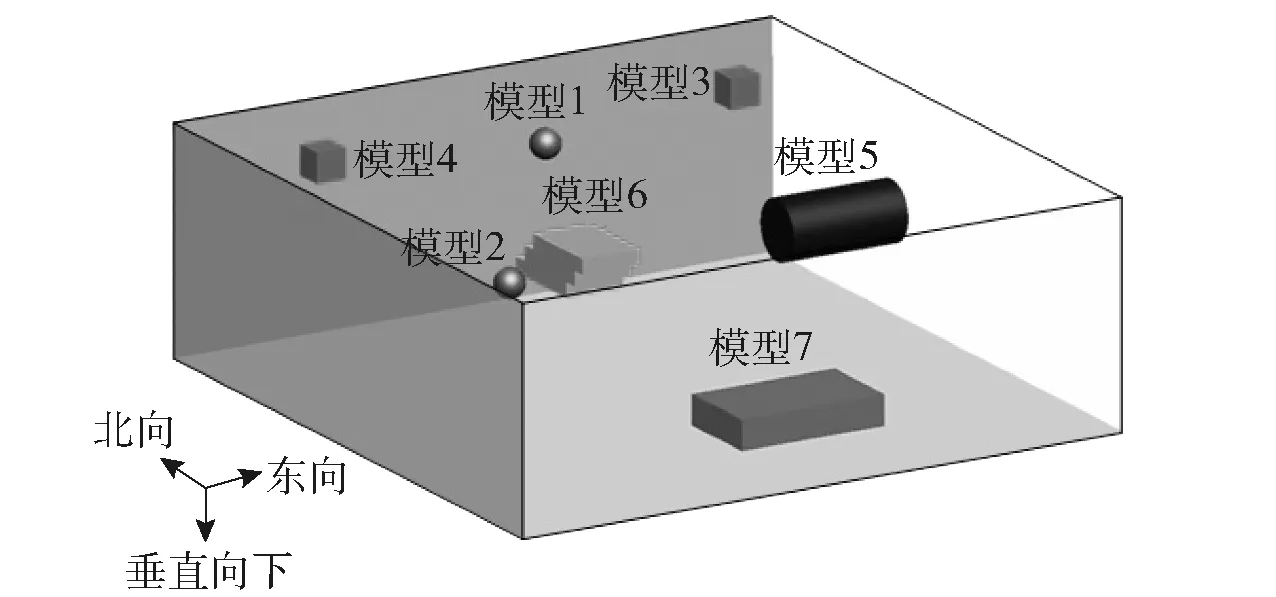
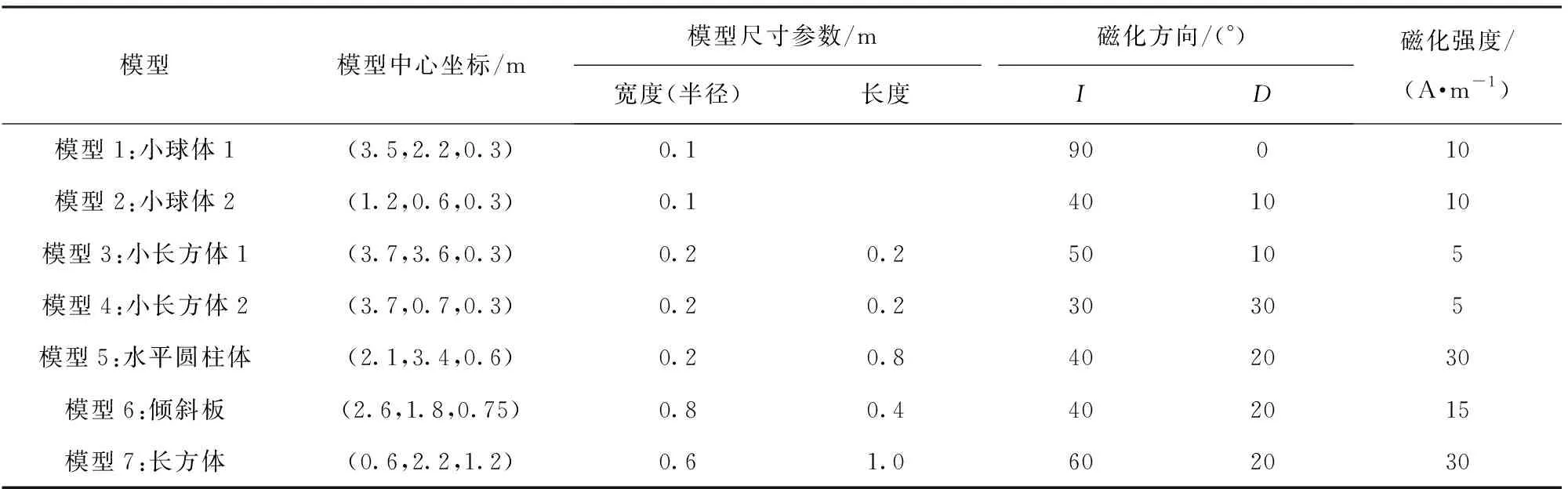
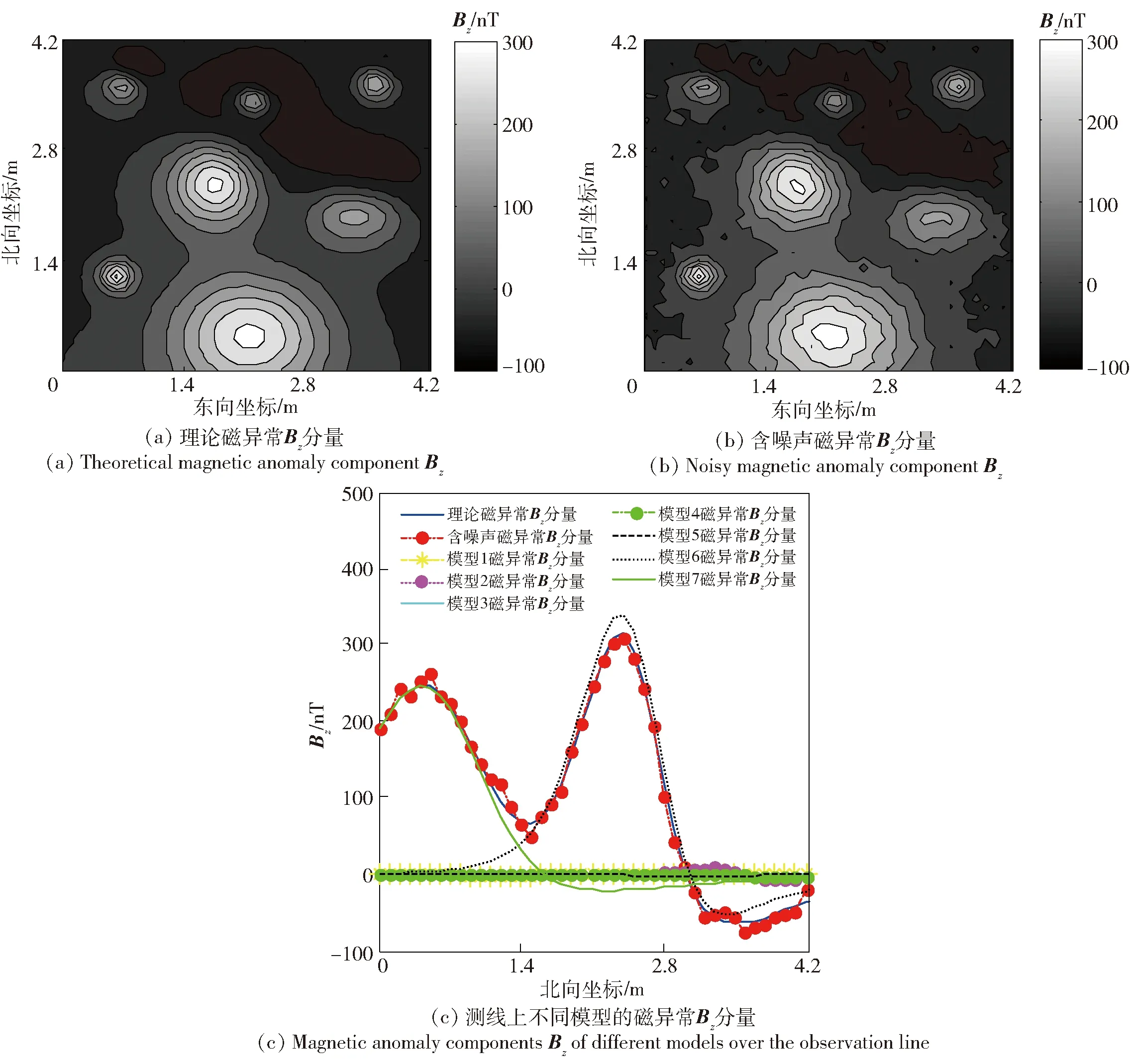
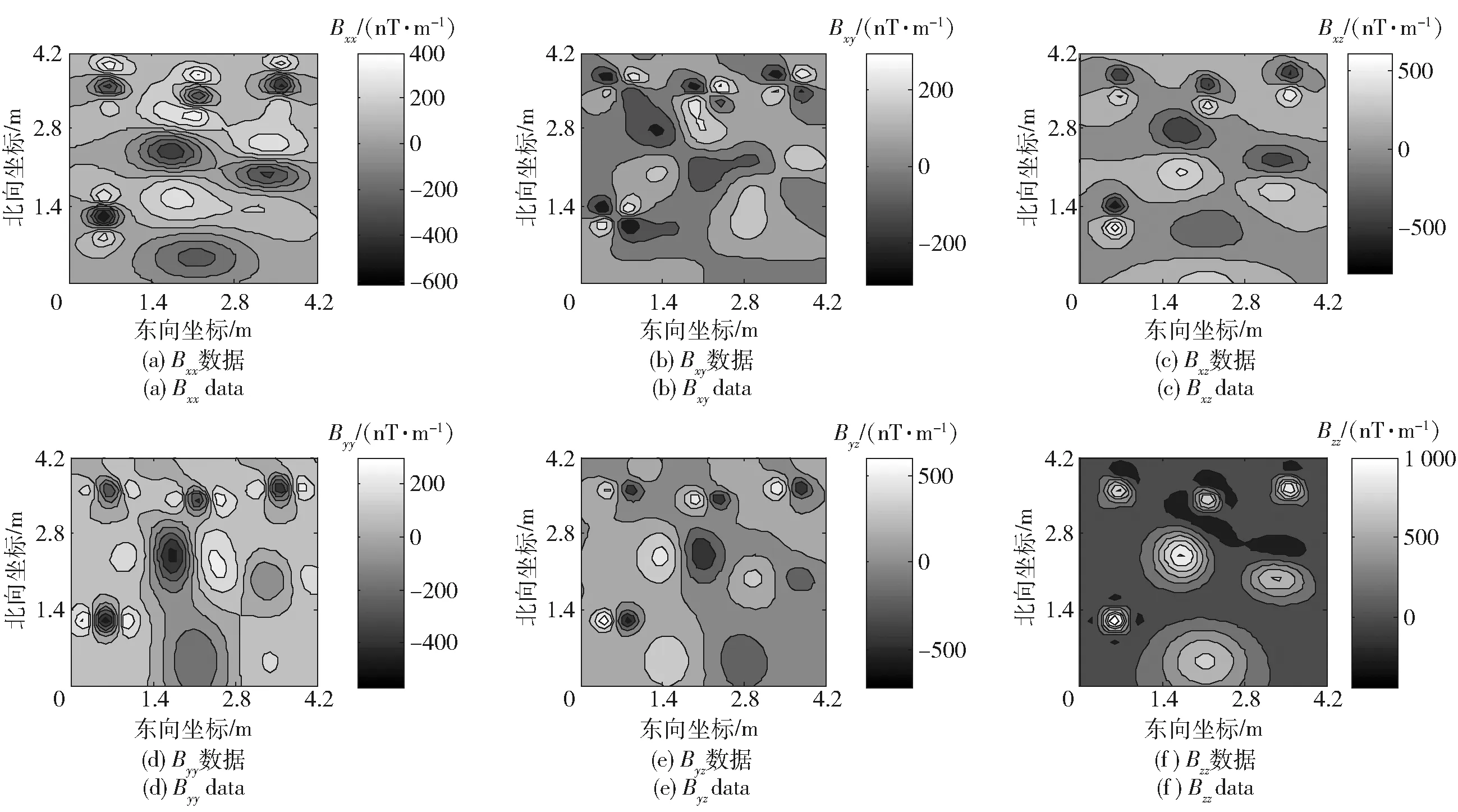


2.2 不同方法的计算精度对比
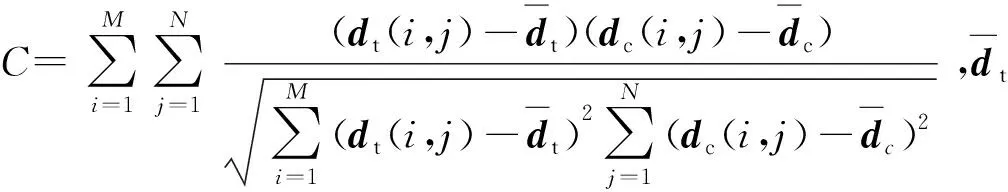

3 试验验证
3.1 待测模型及本文参数选择
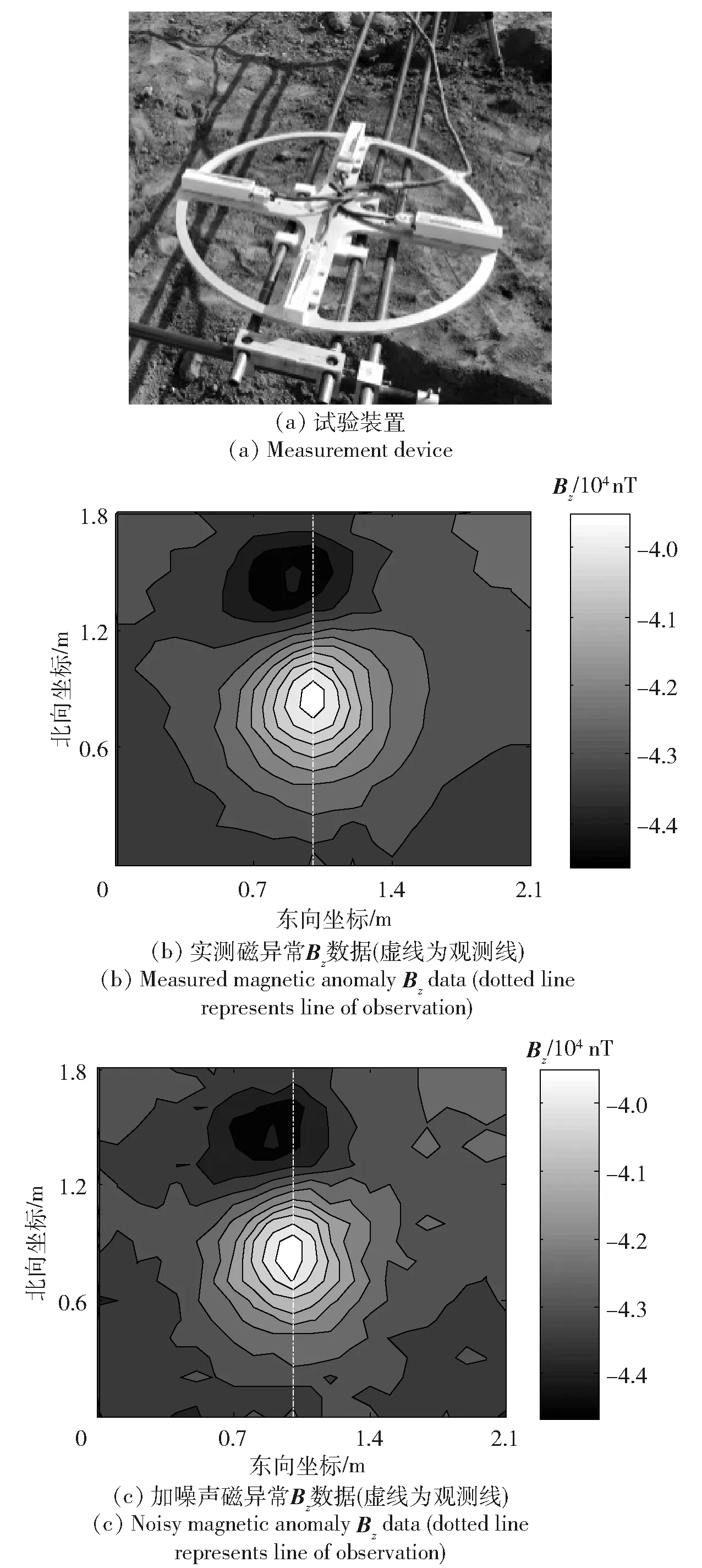
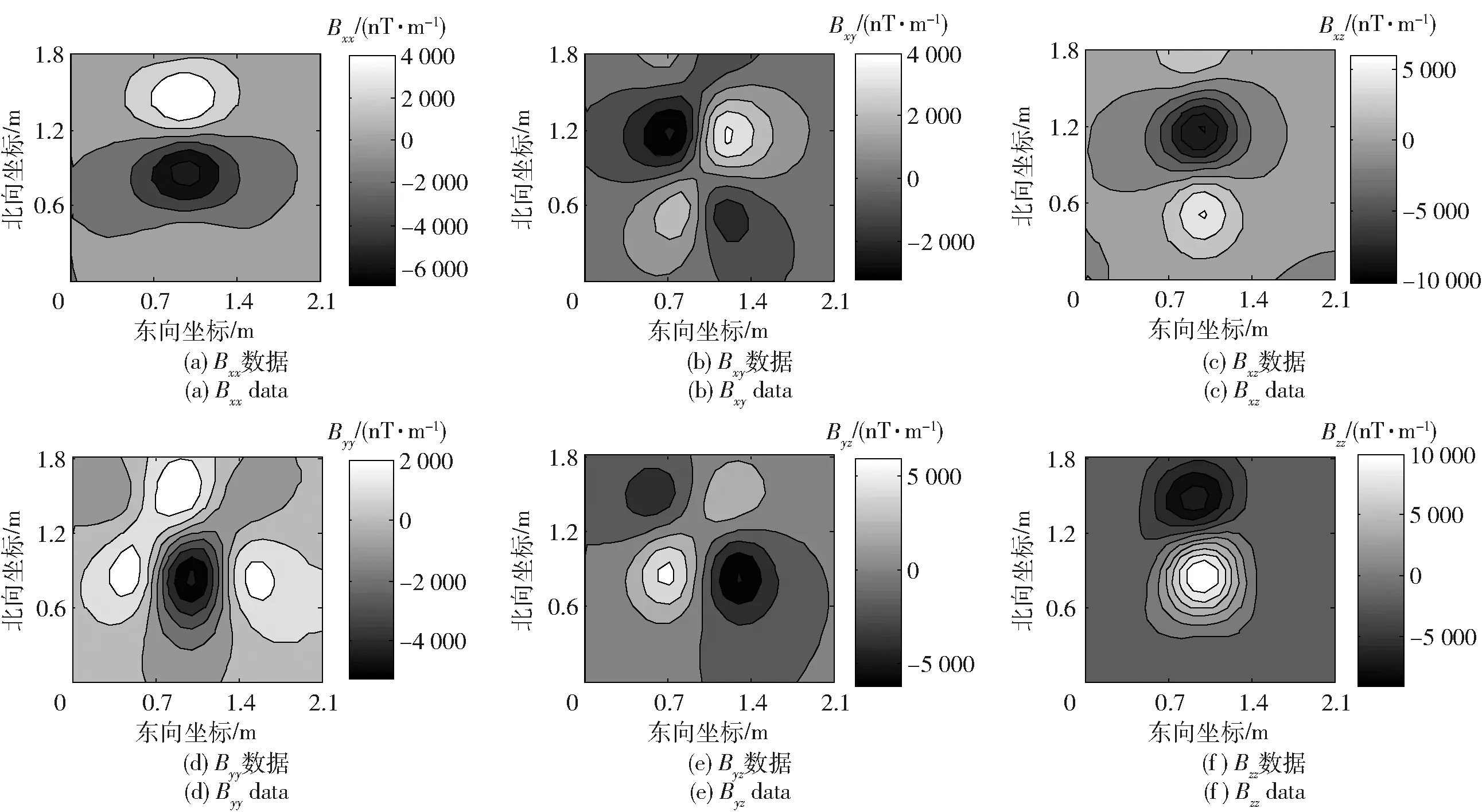
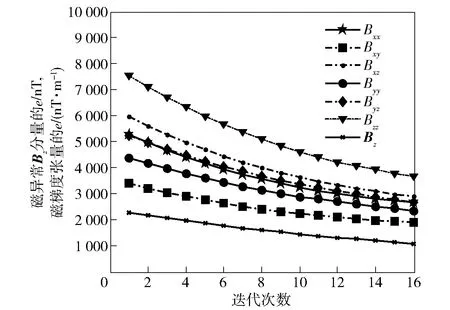
3.2 不同方法的计算精度对比
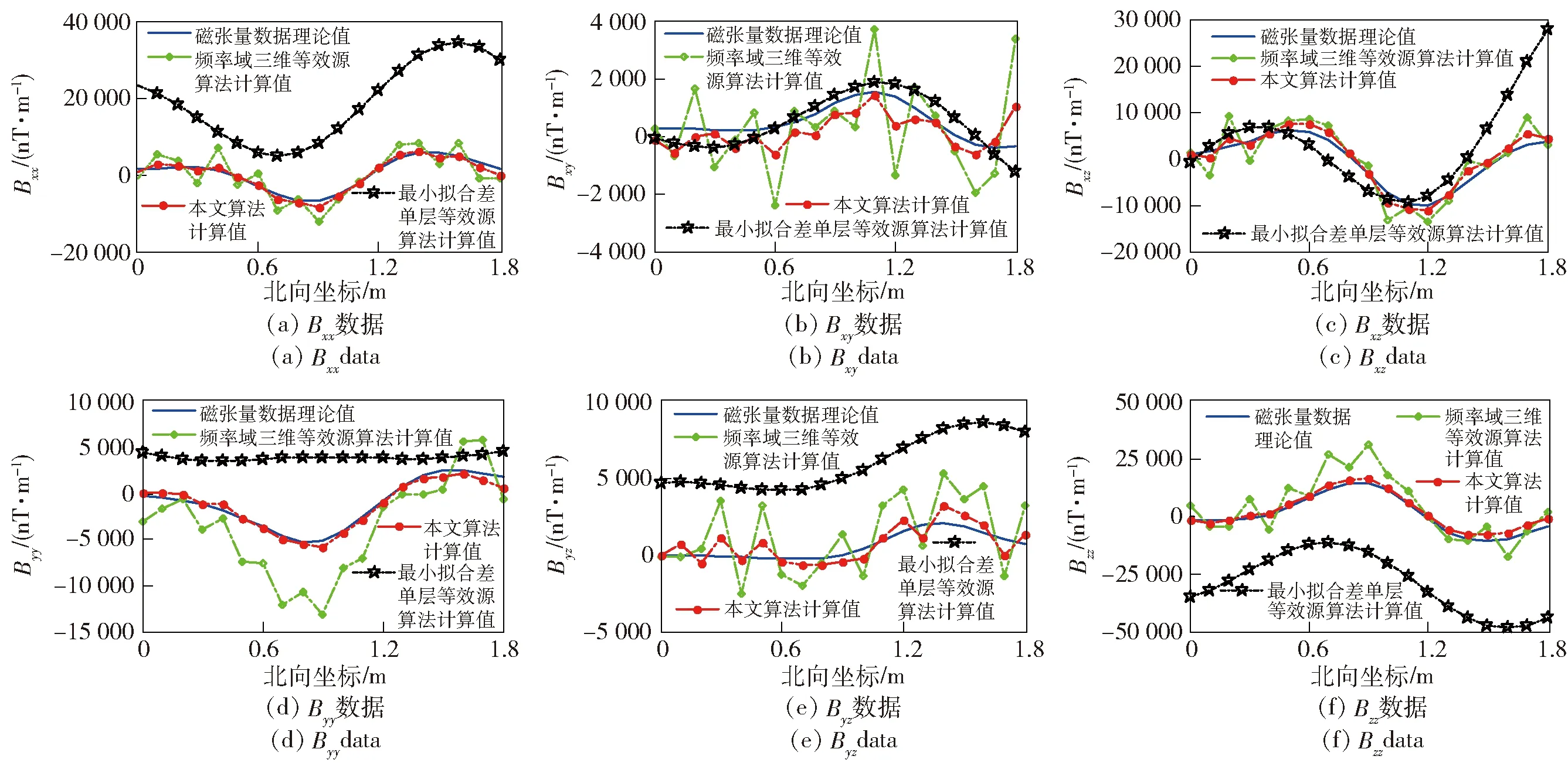
4 结论