从一题多解思考学生解题能力的培养

广东省广州市南沙区教育发展中心(511458) 黄安锦

近日,广州市南沙区初中毕业班学业水平适应性测试中考查了这样一道题,看起来不难,但却在考试中难倒了不少学生,学生觉得试题中的情境很熟悉,却难以找到问题解决的突破口,究其原因是学生在学习中习惯于常见几何模型地死搬硬套, 对题目中的已知条件和结论未能搭建互通桥梁,解题思路不能完整呈现.下面我们通过本题的几种解法,分析题目中所蕴涵的数学源知识的重新建构与综合应用,以找到提高解题的能力的方向.

1 题目呈现

如图1,AB为⊙O的直径, 点C为弧AB中点, 连接AC、BC.

(1) 利用尺规作图, 作出∠BAC的角平分线, 分别交BC、⊙O于点D、E,连接BE.(保留作图痕迹,不写作法)

(2)若BE=2,求AD的长度.

试题分析: 本题的第(1)问主要考查学生利用尺规作图作处角平分线及合理标识点和线段.学生对此类作图题游刃有余.而第(2)问涉及圆的基本性质、辅助线的合理添加、三角形的全等及相似判定等相关知识,对学生转化思想和数学建模思想进行了考查.此题存在多种解题思路,解题的入口较宽.从题目及第(1)问的结论(如图2)中,不难获取以下基本信息:

①由线段AE平分∠BAC,可得∠BAE=∠CAE;

②由AB为⊙O的直径,且点E、点C在⊙O上可得∠AEB=∠ACB=90°;

③由点C为弧AB中点可得AC=BC、∠ABC=∠BAC;

④由圆周角定理可得∠CAE=∠CBE.

本题中涉及的数学源知识有角平分线的定义及性质,圆的基本性质,圆周角定理及其推论,弦、弧、圆周角定理等,我们不妨从这些学生熟悉的源知识入手,探寻解决问题的方法.

图1

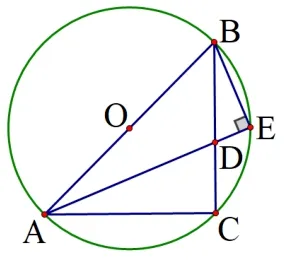
图2

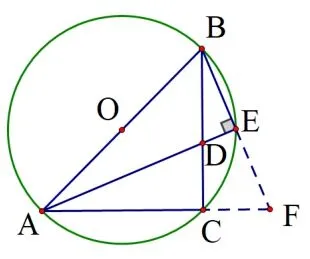
图3

2 解法分析

解法一如图3,由AE平分∠BAC,根据角平分线的定义可得∠BAE= ∠CAE,结合直径AB所对的圆周角为直角,根据等腰三角形“三线合一”,联想到延长BE、AC交于点F,构建等腰ΔABF,再利用弦、弧、圆周角定理分别得到AC=BC、∠CAE= ∠CBE,进而推证ΔACD与ΔBCF相似,得到AD=BF=2BE=4.

解题反思本方法从角平分线的基本定义入手,通过合理添加辅助线,借助圆的基本性质、等腰三角形的基本性质和全等三角形的判定等基本知识来解决问题.这些知识的再现和综合应用对于提升学生的学生的几何直观想象能力及数学建模的能力起到很好的促进作用.

解法二如图4,由AE平分∠BAC,根据角平分线的基本性质,不难想到过点D作DF⊥AB于点F,直径AB所对的圆周角∠C= 90°,得到DF=CD.不妨设DF=x,根据点C为弧AB的中点,且∠C=90°,易知道ΔABC和ΔBDF均为等腰直角三角形,所以BD=AB=利用角平分线定义及弦、弧、圆周角定理得到∠BAE= ∠CAE= ∠CBE, 从而容易推证ΔABE与ΔBDE相似,再根据相似三角形的性质有求得最终得到AD=AE－DE=4.

解题反思本方法从角平分线性质入手,结合特殊三角形及相似三角形的性质定理,通过设置未知数,通过数形关系使本问题由繁化简,由抽象化具体,在解题过程中渗透了数形结合的思想,利于学生的思维拓展.

解法三如图5, 由AE平分∠BAC, 可得∠BAE=∠CAE, 由此可知点E为弧BC的中点, 连接OE, 交BC于点F, 通过垂径定理的推论还可以知道OE⊥BC,BF=FD=再利用ΔBEF与ΔACD相似,通过求出AD=4.

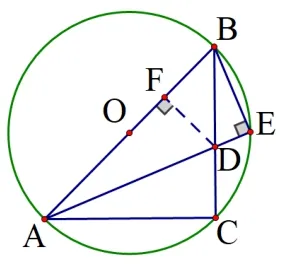
图4

图5

图6

解题反思本方法从圆的基本性质入手,通过垂径定理及其推论和弦、弧、圆周角定理搭建相似三角形的模型,将所求线段与已知线段通过相似三角形紧密联系一起,最终解决问题,本方法强调从结论需求逆向寻找所需的源知识,有利于加强学生的综合分析能力.再者本方法对数学圆内“蝴蝶形”相似模型非常熟悉的学生对于“如何从多样的条件中合理选择解决问题的方案”带来了更深刻的思考,有利于学生数学思维的发展.

解法四如图6, 在AE上作点F, 使AF=CF, 连接CE.根据“等边对等角”和三角形外角性质不难得到∠EFC= 2∠FAC= 45°, 又因为AE平分∠BAC, 结合再根据圆周角定理的推论和弦、弧、圆周角定理可得∠AEC=∠ABC=45°,BE=CE,由此可推证ΔEFC是等腰直角三角形,则有CE=CF=AF=BE=2,进而求出再利用ΔABE与ΔBDE相似求出则AD=AE－DE=4.

解题反思本方法从图形的特殊性出发,从特殊三角形特殊角的半角问题通过构建特殊角,并借助圆的基本性质将已知线段BE 进行等价转化,使图中的位置线段的长度明朗,为后面的相似比求未知线段的长铺设条件.本方法发展学生空间观念、推理能力和创新意识起一定的促进作用,加强学生在解决数学问题中对源知识的挖掘和综合应用,培养学生的应用意识.

3 对学生解题能力培养的思考

课程标准中强调对学生“四基”的培养,关注学生在问题情境中全身心的积极参与思考,在学习过程中促进学生“四能”的培养.在教学中,教师要避免担心学生不会而急于暴露问题解决的线索或思路,应鼓励学生尝试从不同的角度对问题的分析与解决进行思考,体验问题解决的多样性,并通过变式训练强化学生解决问题的能力.解题能力并不是一朝一夕生成的,很多教师在日常教学中过分强调解题的基本模型与套路,通过大量的重复练习让学生变得“娴熟”,如上题,很多学生从图形的表面特征中发现了“8 字相似形”,然而他们却忽略了解题中的目标意识,也就是本题需要探究的结论是什么? 结论的实质又是什么? 题目中隐含那些基础源知识?这些源知识跟所探究的解困存在怎样的依存关系等等,所以很多学生找不到解决问题的突破口, 无法搭建解题的桥梁,最终导致解题思路的紊乱.

3.1 学生的解题能力首先与学生扎实的数学基础密不可分

如上题中涉及的圆的基本性质、角平分线的定义及性质、相似三角形的判定及性质等源知识,如果学生无法熟练掌握,自然无法综合应用并形成解决策略与方法,一切都是空谈.而源知识的习得就有赖于教师对教材的重视,教学中通过合理的情境创设和教学活动组织让学生亲历教材中的概念、性质、定理和推论的生成过程,帮助学生对数学源知识的识记.同时,通过鼓励学生钻研教材,通过变式训练使源知识得以拓展,促进学生解题思维的发展和延伸.

3.2 学生的解题能力还取决于学生审题能力

审题不仅限于读题,更侧重于已知条件和探究结论间的互联互通,这也是学生能否从中找到解题突破口的关键.日常教学中很多老师习惯带着学生一起做题,帮助学生找出关键信息或条件,甚至直接点破了问题的解决思路,这不利于学生审题能力的发展,当学生在真实独立的解题环境中也容易审题不严或找不到方向,最终导致解题思路无法完整的呈现.在教学中,教师可以引导学生进行探究性的阅读活动,让学生审题过程中尝试读懂题目,找到问题关键词,并对问题的解决提出自己的看法,并通过小组讨论或分享自己的看法,教师适时参与学生的分享并进行针对性的疑惑解答,并组织学生解题思路的总结和呈现.

3.3 培养学生的解题能力需要注重数学思维的延伸

课程标准中强调学生思维品质和关键能力的培养,更鼓励教学中引导学生从多视角、多途径去探索分析和解决问题的思路和方法.教学中的一题多解是有效发展学生高阶思维的重要方法之一,教学中不能只关注模型和套路,更应该引导学生通过追本溯源, 深挖源知识背后所蕴含的数学思想,建立知识间的相互联系和对比分析, 找出解决问题的思路,促进学生数学思维的延伸和发展.