关于三角形中两塞瓦线相交所得的线段比例

2021-01-06广东省深圳市新安中学集团第二外国语学校518100华南师范大学510631钟焕旻

中学数学研究(广东) 2020年24期

关键词：燕尾双峰四边形

广东省深圳市新安中学(集团)第二外国语学校(518100) 华南师范大学(510631) 钟焕旻

1 引言

如图1 是三角形中两条塞瓦线相交的图形模型.

虽然是一个非常简单的图形模型,但在小学高年级和中学低年级阶段的数学竞赛中出现的频率很高.我们在此简单列举几道竞赛真题.

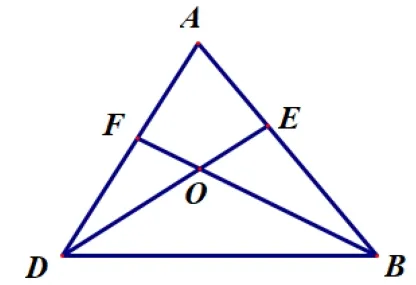
图1

题1(第十届华杯赛初一组总决赛一试第4 题[1])如图2中三角形ABC的面积是60,BE:CE=1:2,AD:CD=3:1,求四边形DOEC的面积.

题2(第十三届华杯赛初一组决赛第11 题[1]) 如图3所示,E,F是三角形ABC边上的点,CE与BF相交于点P.已知三角形PBC的面试是12,且SΔEBP=SΔF P C=S四边形AEP F,求三角形EBP的面积.

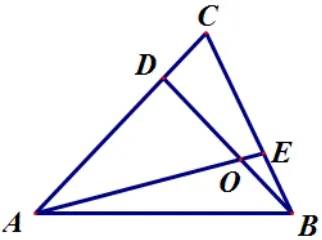
图2

图3

题3(第十八届华杯赛初一组决赛B 卷第5 题[1])如图4 所示, 三角形ABC中,E,F分别是边AB,AC上的一点,CE,BF相交于点P, 已知SΔEBP=SΔF P C=S四边形AEP F=4,则三角形PBC的面积是( ).

题4(2017年第十五届小学希望杯全国数学邀请赛第一试6年级第8 题[2])如图5,点E,F是三角形ABC边AB,AC上的点,线段CE,BF交于点D.若三角形CDF,三角形BCD, 三角形BDE面积分别为3, 7, 7, 则四边形AEDF面积为____.

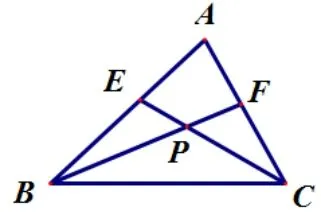
图4

图5

我们可以在这几道竞赛真题中看到,在这个图形中,常考察的是面积和线段比的计算.张景中院士所提出的共边定理就是解决面积和线段比问题的强有力工具.在本文中,我们就将使用共边定理的四种图形形式来对这种类型的问题给出通解通法.

2 基本概念及相关性质

定义1[3]连接三角形的一个顶点和它的对边(或延长线)上一点(非端点)的线段称为塞瓦线.

定理1[4]如图6, ΔABC、ΔABD和ΔACD等高, 则BC:BD:CD=SΔABC:SΔABD:SΔACD;

证明见文献[4].

图6

等高模型是共边定理的理论基础.张景中院士所提出的共边定理正是由等高模型证明得到的.

图7

定理2[5](共边定理)若直线AB与PQ交于点M, 如图7,有四种情形,则有

证明[5]

为了方便记忆,人们对共边定理中的四种图形赋予了生动形象的模型名字.我们简要地介绍如下.

2.1 风筝模型

风筝模型是在任意四边形内的一个图形模型,因四边形的两条对角线相交形似“风筝骨架”,故得名风筝模型.风筝模型是定理1 共边定理中情形(1)的图形.即如图7(1).此处需注意风筝模型和筝形的区别.筝形是对角线相互垂直的四边形,而风筝模型是任意四边形内部两条相交的对角线形成的.可以说筝形是风筝模型的一种特殊情形.

定理3如图8,在四边形ABCD中,点O是对角线AC和BD的交点,则有以下结论:

(1)(共边定理图7 情形(1));

(2)(共边定理图7 情形(1));

(3)S1×S3=S2×S4.

证明(1) 和(2) 的证明见文献[5].由等高模型有故交叉相乘即可得S1×S3=S2×S4.

图8

图9

2.2 燕尾模型

如图9 中,在ΔABC中任意两种颜色的阴影部分组合起来都如同燕尾的形状,故称之为燕尾模型.共边定理中的图7(2)就是燕尾模型.所以燕尾模型是共边定理.

定理4如图9,若点O是三角形ABC内部任意一点,连接AO并延长与BC交于D点,连接BO并延长与AC交于E点,连接CO并延长与AB交于F点,即三角形ABC中的线段AD,BE,CF交于一点O.

(1)(共边定理图7 情形(2));

2.3 双峰模型

双峰模型就是共边定理1 中的第四种图形的体现.在以往的小学高年级和中学低年级阶段的数学竞赛的平面几何试题中出现频率较少.但双峰模型的结论可以给直线形图形中求解线段比和面积比带来极大的简便.

图10

此图形被称为双峰模型的原因是两个三角形ABC和DBC像两座山峰一样.它们以共同的“山底”BC为底,然后“山顶”顶点A,D连线和“山底”的延长线相交,所得到的线段AE,DE的比例等于两个三角形的面积之比.这样从图形的特点出发,给予生动形象的命名.

鉴于小学高年级和中学低年级阶段的同学心智还比较不成熟,故使用贴近生活,生动形象的命名可以帮助同学们激发学习兴趣,从而更好地记忆共边定理的各个形式.另一方面,在竞赛题的图形中,也能更快地找到对应的图形以及其中的数量关系,从而使用共边定理给出简洁的解答.

3 例题详解及推广和变式

例1[5]AD是ΔABC边BC上的中线,过点B任意做一条直线交AD于点E,交AC于F,证明

图11

图12

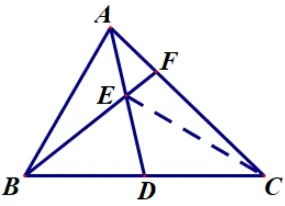
图13

证明一(风筝模型)如图12,连接DF,由风筝模型和等高模型有

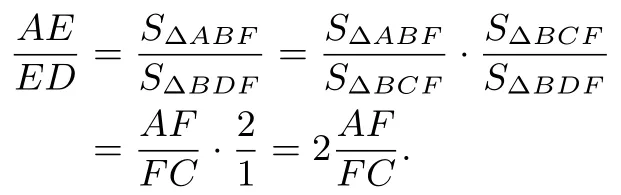
证明二(燕尾模型)如图13,连接CE,由燕尾模型和等高模型有

我们将例1 推广.

问题1如图13,已知的值.

图14

图15

图16

解法一(风筝模型)如图15,由风筝模型和等高模型有

解法二(燕尾模型)如图16,由燕尾模型和等高模型有

评注当我们已知三角形边上的比例时,可以借助风筝模型或燕尾模型以及等高模型,以面积比例为中间桥梁,求得两相交的塞瓦线上的线段比.

反过来,如果我们知道两相交的塞瓦线上的线段比,同样也有两种方式可以求得三角形边长上的线段比.

我们对上面的问题进行变式.

问题2如图14,已知的值.

解法一(双峰模型)如图15,由双峰模型和等高模型有

从而有

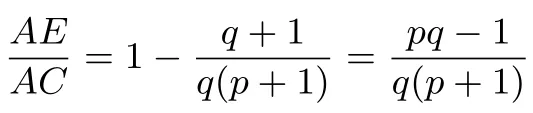
由双峰模型和等高模型有

从而有

解法二(燕尾模型)如图16,由共边定理的有

所以

由燕尾模型有

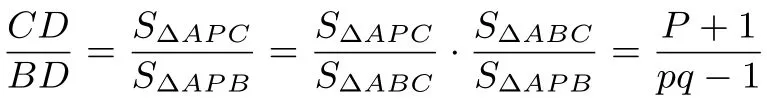
在问题1 中,我们是已知了三角形两边上的线段比,可以利用风筝模型和燕尾模型来求解三角形内的两条塞瓦线上的线段比.问题2 的已知条件和待求问题正好与问题1 是相反的.已知条件是三角形内两条塞瓦线上的线段比,待求问题是三角形两条塞瓦线所对的两边上的线段比.我们可以应用双峰模型(共边定理的第四种图形形式)还有共边定理的第三种图形形式和燕尾模型给出两种解决方法.我们在问题1 和问题2 的解决过程中将共边定理的四种形式都展示了出来.

可见本图形三角形内两塞瓦线相交的图形模型,虽然看着简单,但蕴含了丰富的数量关系.

我们还可以进一步思考,如果在本图形模型中,已知三角形一边长上的线段比和某塞瓦线上的线段比,可否求出另一条边上的线段比和另一条塞瓦线上的线段比呢? 是可以的.

问题3如图14,已知的值.

解法一(风筝模型)如图15,由风筝模型和等高模型有

解法二(燕尾模型)如图16,由燕尾模型和等高模型有

问题4如图14, 若已知求的值.

解法一(双峰模型+风筝模型)如图15,由风筝模型有所以SΔABE=pSΔBDE,由等高模型有所以SΔADE=aSΔCDE,

由双峰模型有

解法二(燕尾模型)由共边定理有由燕尾模型有=a,所以

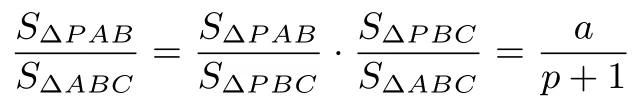
所以

故由燕尾模型有

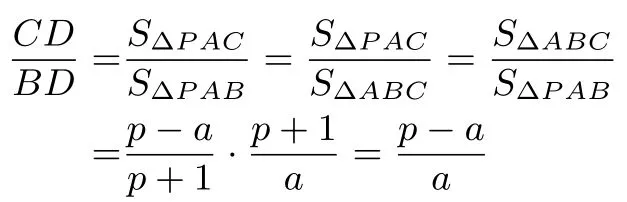
另一方面由共边定理(3)有

由以上四个问题我们可以发现在三角形内两塞瓦线相交的图形模型中,只要知道了三角形两边上的线段比和两塞瓦线上的线段比这四组线段比中的两组,就可以求出另外两组线段比.为了叙述的简便性, 我们将三角形的边称为“外边”,将塞瓦线成为“内边”.称“内边”AD与“外边”BC是相对的位置关系,称“内边”AD与“外边”AC是相邻的位置关系.同理可知BE与AC相对,BE与BC相邻.我们可以将解题思路简要地通过下面的三个流程图进行总结.