坐标法PK几何法——2019年天津卷理第17题

苗 壮

(江苏省南京师范大学附属扬子中学 210000)

立体几何中的空间角问题，往往可以比较集中地考查考生的空间想象能力、逻辑推理能力、运算求解能力等，历来为高考命题者所垂青，几乎年年必考，只是改变命题背景、考查角度等.立体几何中的空间角问题是异面直线所成的角、直线和平面所成的角以及二面角的平面角三者的总称，破解基本思维方法就是几何法或坐标法等.

一、真题在线

【高考真题】(2019·天津卷理·17)如图，AE⊥平面ABCD，CF∥AE，AD∥BC，AD⊥AB，AB=AD=1，AE=BC=2.

(1)求证：BF∥平面ADE；

(2)求直线CE与平面BDE所成角的正弦值；

本题以一个非特殊的立体几何图形为问题背景，结合空间线面平行的判定、直线与平面所成的角的求解、二面角的平面角的应用等三个部分来设置问题，把立体几何中的线面判定问题、空间角问题、空间距离问题这三个最重要的问题加以合理交汇与融合，综合考查考生的数学知识与数学能力.

二、真题解析

解析方法1：(官方标答——坐标法)

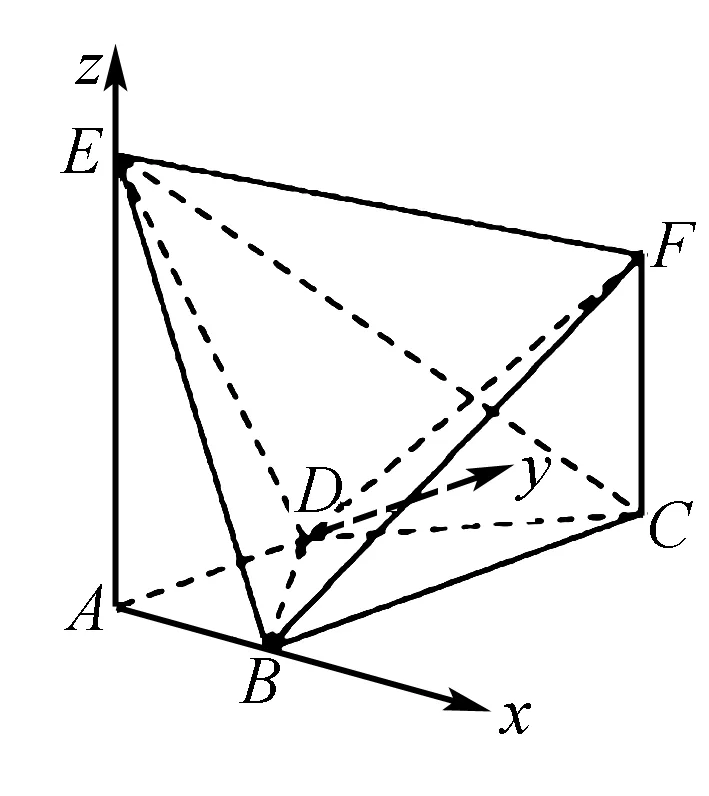
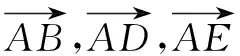
设CF=h(h>0)，则F(1，2，h).

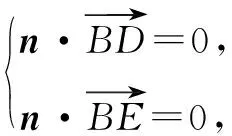
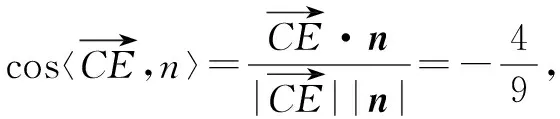
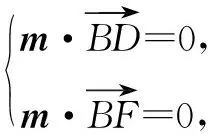
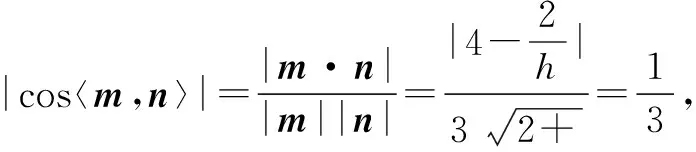
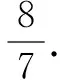
点评利用坐标法破解空间线面角的步骤：①确定直线的方向向量和平面的法向量；②求两个向量夹角的余弦值；③确定向量夹角的范围；④确定线面角与向量夹角的关系：当向量夹角为锐角时线面角与这个夹角互余；当向量夹角为钝角时，线面角等于这个夹角减去90°.利用坐标法破解空间二面角的步骤：①确定两平面的法向量；②求两个法向量夹角的余弦值；③确定向量夹角的范围；④确定二面角与向量夹角的关系：二面角的范围要通过观察图形来确定，法向量一般不能体现出来.

方法2：(几何法)

(1)因为CF∥AE，AE平面ADE，所以CF∥平面ADE.因为AD∥BC，AD平面ADE，所以BC∥平面ADE.又BC∩CF=C，所以平面BCF∥平面ADE.而BF平面BCF，所以BF∥平面ADE.

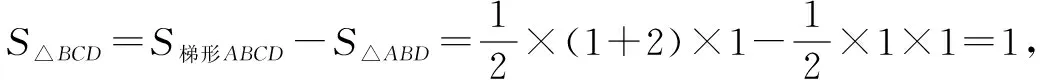
(3)分别取BD、BC、BF的中点H、M、K，连接EH、HK、AH、HM、KM、EK、MD.

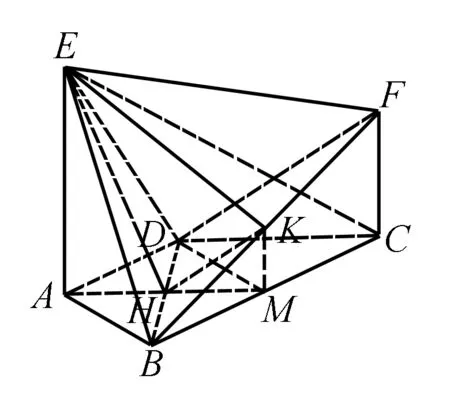
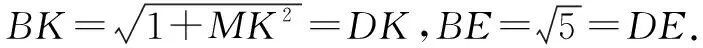
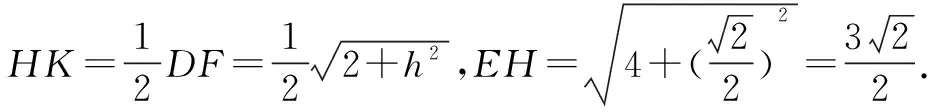
点评利用几何法破解空间角问题(包括异面直线所成的角，直线与平面所成的角，二面角的平面角问题)，关键是抓住相应空间角的概念，作出相应的空间角，再通过回归平面几何问题，在相应的平面三角形中通过解三角形问题来解决相应的空间角问题.当中涉及一些概念说明，逻辑推理等问题，要交代清楚，不能遗漏.特别一些必要的辅助线的构造，为空间角的确定提供条件，也是破解相应空间角问题的难点所在.

三、解后反思

立体几何中涉及空间角的问题，在高考中经常出现，从学生答题看，解题中对于异面直线所成角、直线与平面所成角，二面角的平面角等，涉及坐标法切入时，要合理构造相应的空间直角坐标系，利用空间向量的坐标运算来确定相应的空间角，要注意所求解的空间向量的夹角与实际所要求解的空间角之间的关系；而涉及几何法切入时，不加论述证明就直接计算或利用所成角，是比较普遍的错误，务必注意纠正，在用所成角或证明前都必须依据定义先说明为何那角就是所成角，通过逻辑推理再加以合理应用.