提高学生高考物理实验解题能力
——以实验“纸带求加速度”为例方法归纳、错误分析
2021-01-04鲁同心
鲁同心
(江苏省清浦中学 223001)
在“探究小车速度随时间变化的规律”的实验中,要求学生通过对纸带打出点的数据处理,测量小车瞬时速度和小车运动的加速度.这已经成为考试的热点之一.
一、方法归纳
笔者对加速度计算的方法做如下归纳:
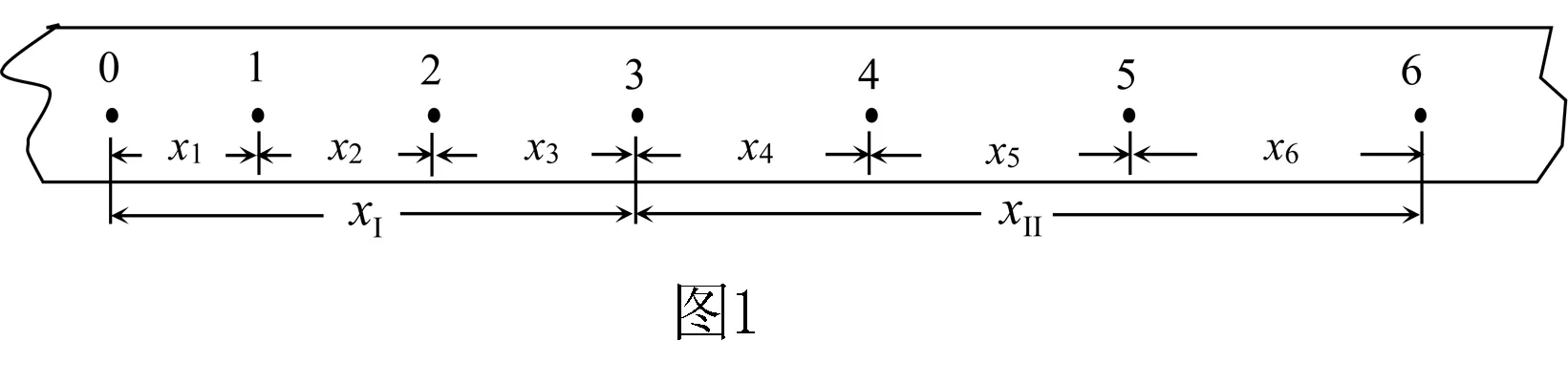
为了有效减少测量加速度时的偶然误差,应用该公式进行数据处理.选择合适的计算方法,真正减少实验误差.常见方法如下:
方法1 运用公式Δx=aT2计算.
Δx=x2-x1=x3-x2=……=aT2,即任意两个相邻相等的时间T内的位移之差Δx=aT2.
利用xm-xn=(m-n)aT2求解,如果纸带给出的数据不是连续的两段位移,如目前只知道x2和x5,则可以有x5-x2=3aT2.
方法2 利用“逐差法”或“两段法”计算.
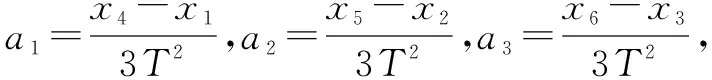
由于采用将打点纸带分成两大段来处理即“两段法”求运动物体的加速度会更准确,计算也较简便,建议教师在教学过程多介绍“两段法”即,
xⅡ-xⅠ=at2(其中t=3T).
无论从实际的实验操作时的数据采集,还是从减小误差的角度,或者从数据处理的方便,“两段法”均为最佳方法.
二、学生常见错误类型统计
加速度的计算成为考试中的经典,学生也能掌握一定的处理方法.但仍然很容易出错.笔者对历次考试中不同类型的学生“纸带的加速度计算”错误类型做了统计如下:
1. 时间间隔T没有判断正确,每段位移的间隔一般为T=0.1s或者T=0.02s.
2. 计算时未将数值换算为国际制单位m.
3. 有些题目物体做匀减速直线运动,学生定向思维,未考虑加速度为负.
4. 未按题目要求选取有效数字的位数.
5. 计算的方法并没有准确掌握.
三、几种典型情况
1.直接利用公式求解
例1 在《探究小车的速度随时间变化的规律》的实验中,给出了这次实验中的一条纸带,如图2所示,其中0、1、2、3、4、5、6都为计数点.从0点开始,每相邻两个计数点之间的时间间隔为0.1 s,测得:x1=1.40 cm,x2=2.00 cm,x3=2.60 cm,x4=3.20 cm,x5=3.80 cm,x6=4.40 cm.

则小车的加速度为____m/s2.
答案:0.6 m/s2.
点评此类题型由于连续相等时间间隔内的位移差均相等,所以直接利用方法一计算即可.
例2在《研究匀变速直线运动》的实验中,得到一条纸带如图3所示,A、B、C、D、E、F、G为相邻的7个计数点,已知相邻计数点间的时间间隔为0.10 s,则利用图中标明的数据(单位: cm)可得小车的加速度为____m/s2,在打点计时器打出D点时,小车的瞬时速度为____m/s.

答案:1.57 m/s2.
点评此题已知的位移不是相邻的,计算时要注意公式的正确运用.
例3 小球作直线运动时的频闪照片如图4所示.已知频闪周期T=0.1 s,小球相邻位置间距(由照片中的刻度尺量得)分别为OA=6.51 cm,AB=5.59 cm,BC=4.70 cm,CD=3.80 cm,DE=2.89 cm,EF=2.00 cm.小球在位置A时速度大小vA=____m/s,小球运动的加速度为____m/s2.
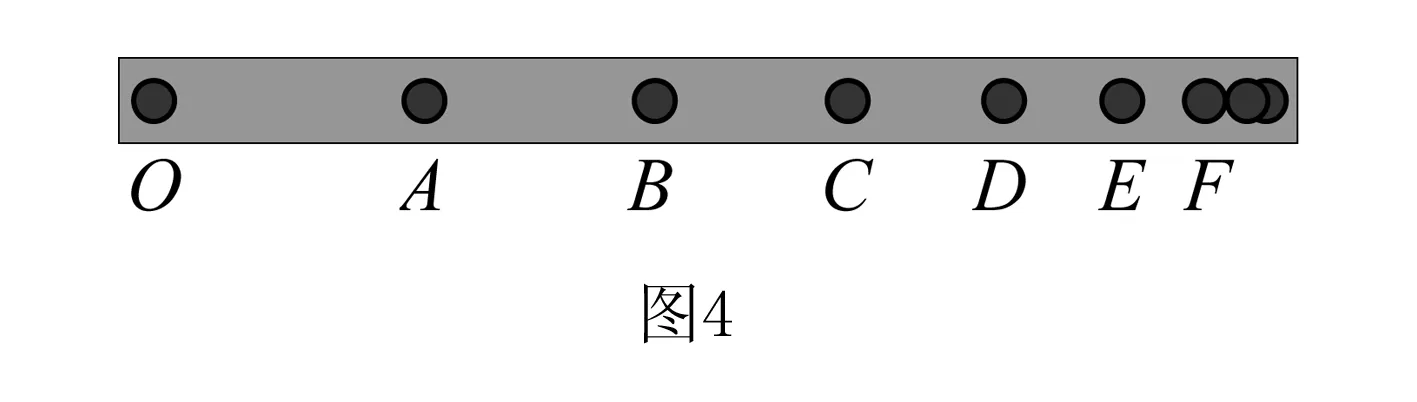
答案:0.605 m/s,-0.901 m/s2.
点评此题是小球做匀减速运动,计算的加速度应为负值.相邻时间间隔的位移差都不完全相等,计算需要使用“逐差法”或“两段法”.本题直接运用“两段法”计算简单又容易理解.另外学生在做题时容易定向思维将加速度写成0.9 m/s2,漏掉负号.
2.利用“逐差法”或“两段法”求解对比
例4 某同学在做“测定匀变速直线运动的加速度”实验时,从打下的若干纸带中选出了如图5所示的一条(每两点间还有4个点没有画出来),图5中上部的数值为相邻两个计数点间的距离.打点计时器的电源频率为50 Hz.由这些已知数据计算:(1)该匀变速直线运动的加速度a=____m/s2.(2)与纸带上D点相对应的瞬时速度v=____m/s.(答案均要求保留3位有效数字.)
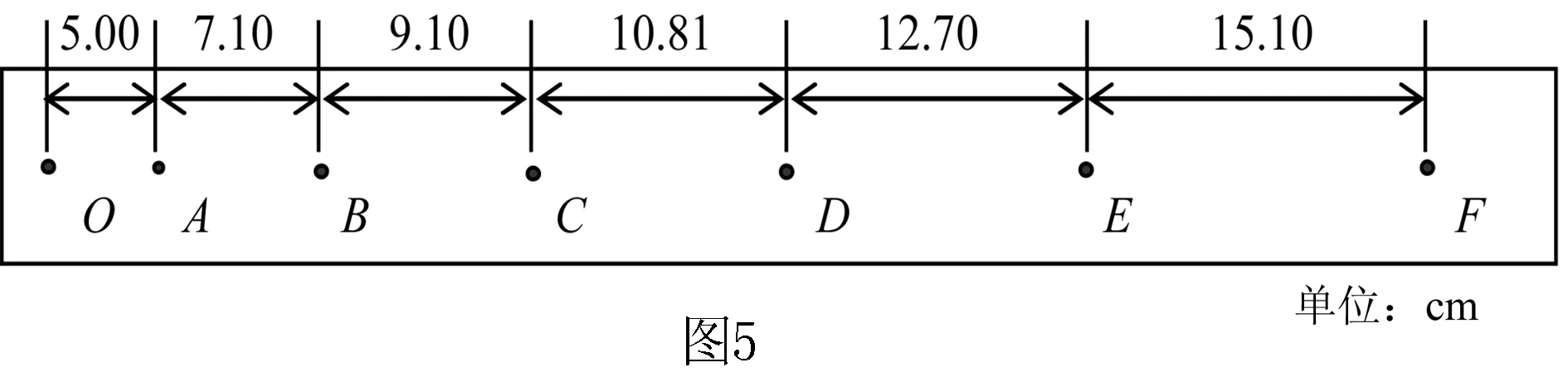
解析相邻计数点间的时间间隔为T=0.10 s.
方法1利用逐差法
方法2利用“两段法”
将OC段看成xⅠ,CF段看成xⅡ,
由xⅡ-xⅠ=at2,(其中t=3T),
=1.93m/s2.
点评本题中如果是奇数段位移,可考虑去掉前面较短的位移,然后在用上述方法处理.两种方法从数学计算上看貌似一样.但细想一下:在实验数据处理时用“逐差法”原理变得较难理解,实验误差更大,计算也更复杂.将纸带分成六段,有的甚至更多,这样做必然使被测量的长度变短,增大了测量的相对误差,这不可能减小实验误差.
此题用“两段法”可以达到同样目的.将打点纸带分成较长的两段来处理,便于数据的测量,公式的理解,结果的计算.此法减小了误差,达到了更好的实验效果.教材中介绍的“逐差法”可以简化为“两段法”.
教师在平时的教学中多找出学生出错的主要原因,将一类题型整合在一起理解,能帮助学生提高解决物理问题的能力,可以起到化难为易,化繁为简,事半功倍的效果.
