基于希尔密码的秘密共享方案

（铜陵职业技术学院，安徽铜陵244000；云南大学，云南昆明650091）

一、秘密共享相关知识

秘密共享是在一组确定的成员之间分配和共享一定的数据信息，该数据信息只有在先前确定的授权用户共同参与下才能得到还原。

秘密共享方法基本上可以分为两条主线：一是采用不同的数学方法，二是应对不同的实际问题需求，本文研究的是后者。

在现实问题中，有些场合需要秘密份额可以重复使用的情况下在同一组参与者中共享一个秘密。本文通过引入希尔密码体制，设计基于希尔密码的秘密共享方案。

二、希尔密码相关知识

（一）希尔密码

希尔密码是一种基于矩阵原理的替换密码，由Letter S.Hill在1929年研发。每个字母由26进制数字替换：如a=0，b=1，c=2，…。一串字母组成的m维向量，与一个m×m 的矩阵相乘后将得出的数值模26，值得注意的是这里用作加密的矩阵（即秘钥）必须是可逆的，不然就不能解密。其实，只需要秘钥矩阵的行列式值与26互质即可。

（二）构造希尔密码体制

取一个矩阵A（保密），要求A可逆，且A的行列式与26互质，取字母表，这里用原始字母表（a=0，b=1，…，z=25）。

根据上述参数，构造希尔密码体制如下：

加密矩阵：A

明文：P转化为小于26的数字序列

密文：C转化为小于26的数字序列

加密算法：C=PA

解密算法：P=CA-1

（三）希尔密码加解密举例

1.加密（由C=PA）

（1）定义字母表

（2）定义一个矩阵A（必须存在逆矩阵）作为加密秘钥，例如：

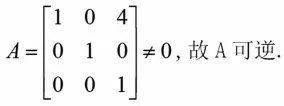
（3）取加密明文，如明文为：I agree.

图1

（4）将需要加密的明文数字化为其对应的字母表里的数字（这里不需要区分大小写）。

（5）将转换后的明文数字序列按照秘钥矩阵的阶数进行分组，如：

（6）每组数字序列和秘钥矩阵行矩阵的乘法运算，结果即为密文矩阵，如：

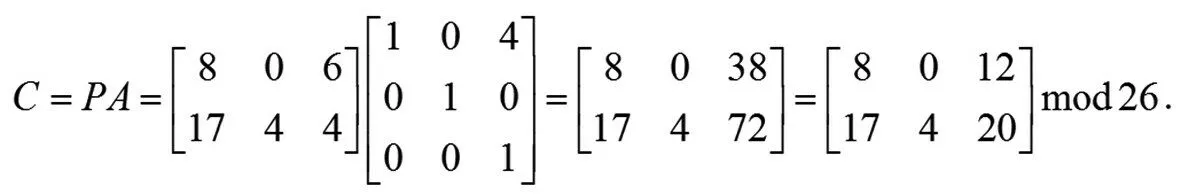
（7）将密文矩阵根据字母表转化为对应的字母（在此要记录下数字在矩阵中的位置），从而得到密文字符串，如：上例的密文字符串为：I a m r e u.

2.解密（由P=CA-1）

（1）在26进制中，求出加密秘钥的逆矩阵，如：

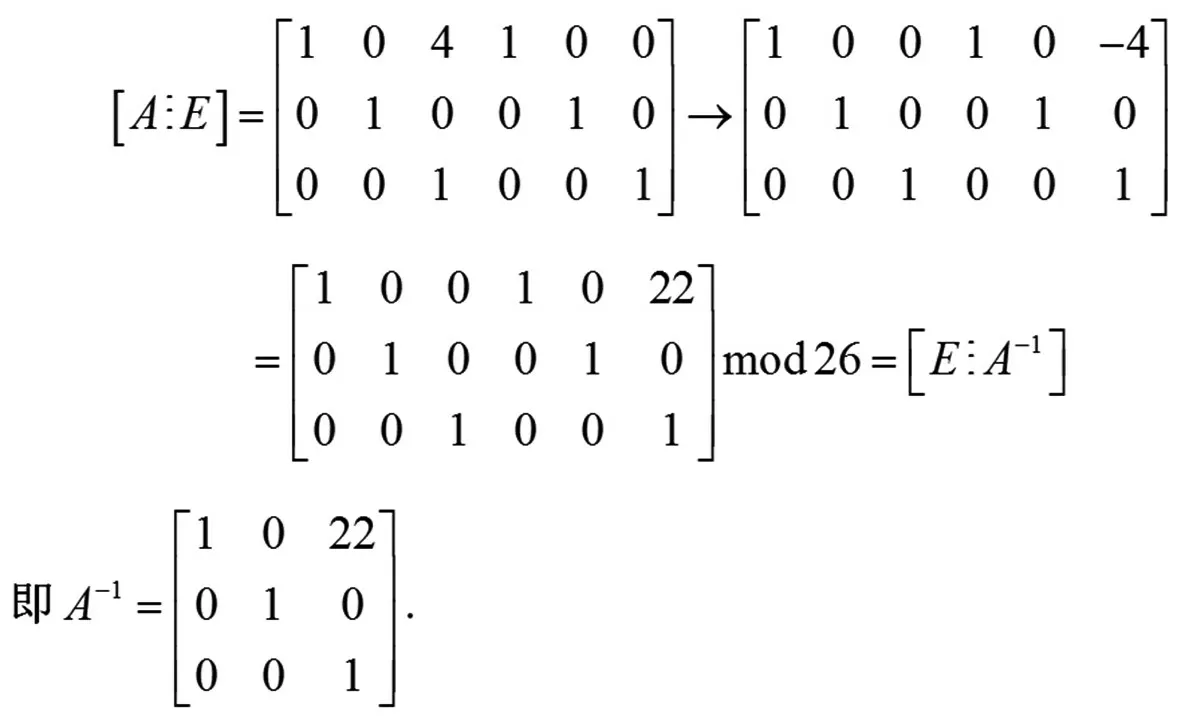
（2）将密文字符串转化为数字序列并按照加密过程中的记录的位置进行分组，如

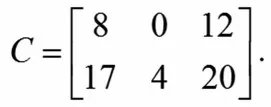
（3）每组数字序列和秘钥矩阵的逆矩阵做乘法运算，如：

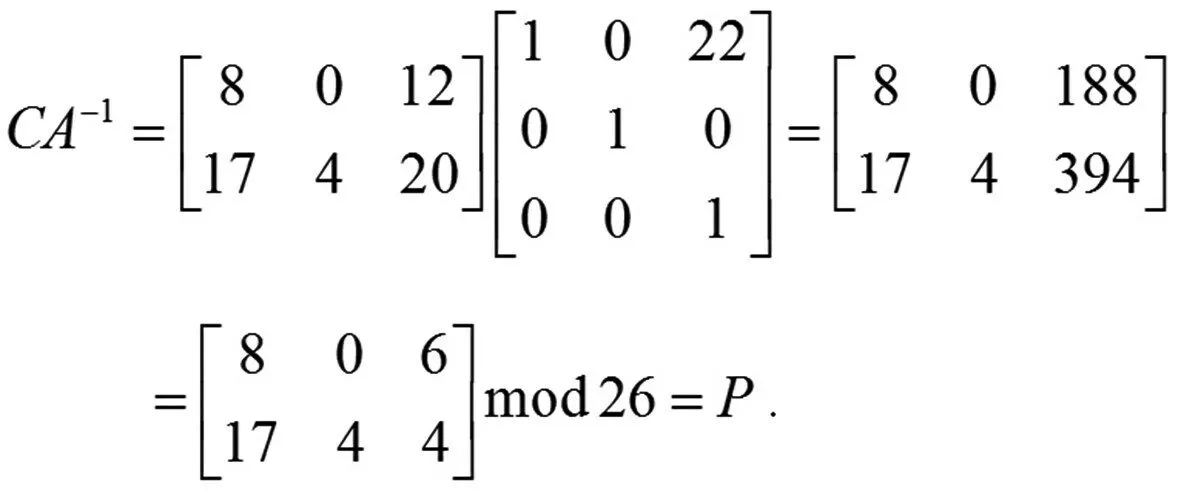
（4）将明文矩阵对应的数字序列根据先前记录的脚码和字母表转化为字母序列，如：I a g r e e .

（5）根据英文组合的常识，得知明文为：I agree.

三、构造基于希尔密码的秘密共享方案

（一）系统初始化及系统参数

设U=（w1，w2，wn）是参与者集合，秘密分发者记为M，秘密计算者记为D（这里D是一台安全的计算机，用来完成恢复秘密的工作），利用逆矩阵加密第一步要将加密的明文数字化，并取数字化后的明文作为明文块。

（二）秘密分发算法

1.随机取一个矩阵A（存在逆矩阵并保密）作为密钥矩阵；2.根据图1将明文字母转换为对应的字母表数字；3 将转换后的明文数字序列按照密钥矩阵的阶数进行分组；4.根据矩阵的乘法运算法则，每组转换后的明文数字序列和秘钥矩阵进行矩阵的乘法运算（如：矩阵乘以矩阵），结果即为密文数字序列；5.将密文数字序列根据图1转化为对应的字母，即为密文字符串，并用脚码标注其在密文数字序列中的位置，将其发给参与者，作为参与者的密码。

（三）秘密重构算法

1.每个合作的参与者输入自己的密码（密码正确能重构，否则不能重构；2.秘密计算者D将收到的密文转换为相应的数字序列；3.秘密计算者D 计算出加密矩阵的逆矩阵；4.秘密计算者D 用密文分组矩阵乘以逆矩阵，结果即为明文矩阵；5.将明文矩阵按照给定的字母表转换为明文字符串（如果不是预先设定的明文字符串，说明参与者输入密码错误）

四、安全性分析与讨论

本文设计的基于希尔密码的秘密共享方案，其安全性是基于希尔密码的安全性。

（一）由于希尔密码采用矩阵运算加密，在给定的明文相同的条件下，加密过程中也可能出现不同的密文，因此，可以很好地抵御字母频率的攻击。

（二）如果是一个非授权用户，存在以下三种情况：

1.若不知道参与者的密码，则签名时不能通过；2.若不知道参与者密码所在密文数字序列中的位置，则签名时不能通过；3.秘密分发者可以根据需要定期随意变化字母表中字母代表数字的位置，增加安全性。