单链形悬挂接触网刚度分布对弓网受流质量影响

2021-01-04

延安职业技术学院学报 2020年6期

（西安铁路职业技术学院，陕西西安710026）

引言

目前，高速铁路的实际最高运行速度已达350km/h（京津城际高速铁路）。随着日本东京到名古屋之间速度为500km/h 的磁悬浮线路的动工兴建，轮轨铁路再一次进行较大幅度提速的可能性增大了。但是，受轮轨和空气激扰的影响，进一步提高列车行驶速度会使受电弓的振动与接触线的波动运动加剧，受电弓与接触线分离的离线现象增加。弓网离线成为影响弓网受流质量，制约列车提速的关键问题。因此，对于较高运行速度（380km/h以上）的弓网离线影响因素及其特性的研究就变得尤为重要。

对于弓网受流特性，国内外诸多学者已进行了很多研究。如张卫华、周宁、梅桂明等人分析了不同接触网悬挂类型及结构参数对弓网接触压力的影响；汪吉健等人分析了不同承力索张力下弹性分布及反射因数对接触线抬升量的影响；Massat 及Lopez-Garcia、J.Pombo 等人分析了运行速度及接触网对离线率的影响。

但是，关于弓网接触压力的研究，在时域方面，基本都采用接触压力平均值、最大值、最小值、标准偏差进行分析。所以，本文采用仿真研究的方法，通过对接触网分布和弓网间接触压力的变化的分析，并采用移动平均值和移动标准差的方法对弓网接触压力进一步分析，为优化接触网设计，降低离线率，提高受流质量提供理论上的支持。

一、接触网与接触压力的关系

（一）弓网耦合模型

采用考虑了接触网弛度、弹性、阻尼等因素的欧拉-伯努利梁模型，以及可以反映受电弓高频振动的三质量块模型，利用商业仿真软件MSC.marc建立的弓网有限元弓网耦合运动系统模型，如图1所示。

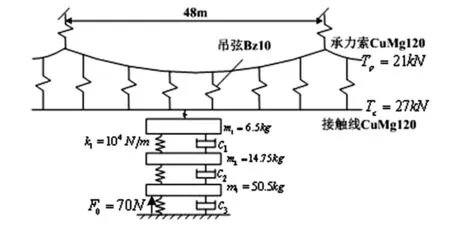
图1 弓网耦合模型结构示意图

图中接触网参数与京津城际高速铁路接触网的设计参数基本一致。受电弓模型是参考SSS400+，将双滑板改为单滑板（滑板质量保持不变）后建立的。

受电弓在垂直方向的运动方程为：

公式中，K0为接触网跨距平均值，ε为接触网跨距的弹性差异系数，L为接触网跨距长度，m为受电弓的质量矩阵，y 为受电弓的垂向位移；c 为受电弓的阻尼矩阵；F0为受电弓的抬升力。可以看出，在接触网结构及张力一定的情况下，接触网的值只与位置有关；而受电弓的垂向位移是由其抬升力及所在位置决定的。

采用图1中所示的接触网-受电弓结构及参数，建立的全锚段简单链形悬挂接触网及单滑板受电弓仿真结构模型如图2所示。

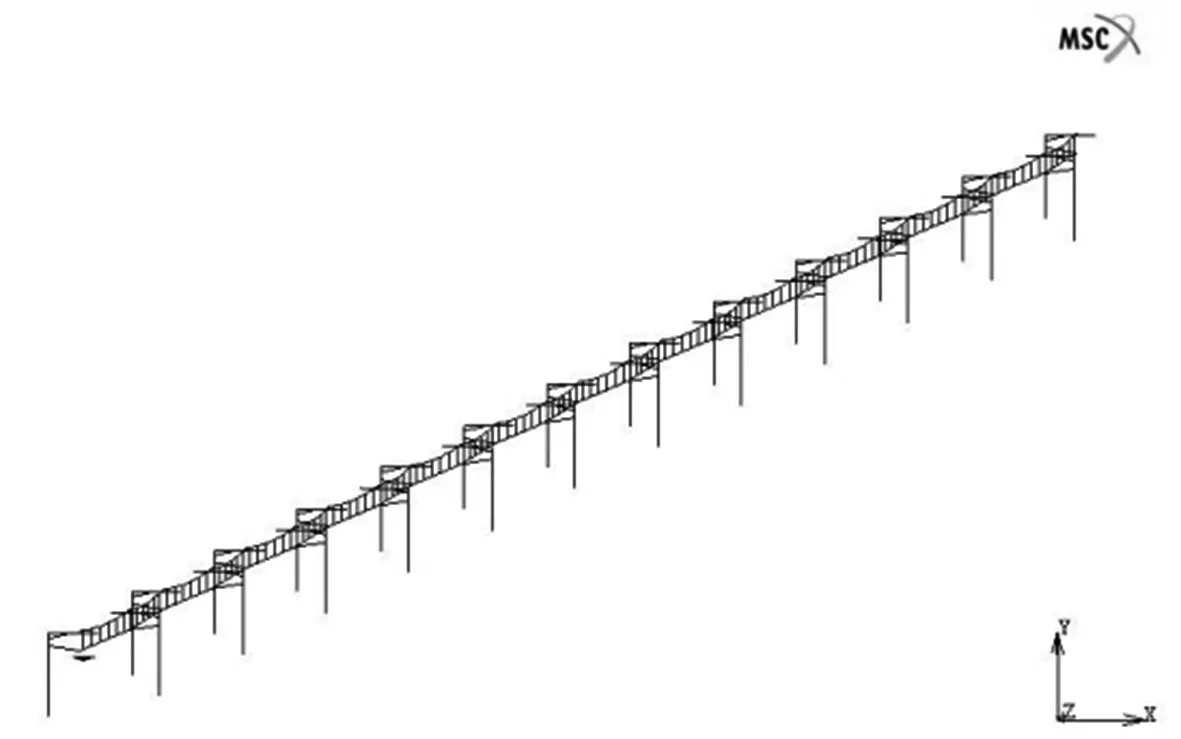
图2 弓网仿真结构模型

（二）接触压力特性研究

在接触网施加张力一定的情况下，接触网的大小主要取决于接触网跨距、材质等结构参数。在第2 节图1所示的弓网模型中，通过受电弓对接触线施加70N抬升力，可以得到接触线的抬升量。根据EN50119标准中的定义，计算出的接触网变化曲线如图3所示。

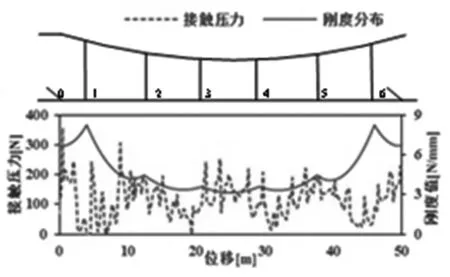
图3 接触网分布曲线

在图3中，1到6分别表示接触线在一个跨距内的6个吊弦悬挂点，0为定位点。

如果以跨距为单位讨论接触网的话，其分布规律主要取决于承力索的弛度。也就是说，由于承力索有较大的弛度，在支柱附近的首末吊弦处（吊弦悬挂点1，6）值最大，跨距中部（吊弦悬挂点3，4）值最小，而定位点0 处的也较大。另外，在首末吊弦（吊弦悬挂点1，6）附近的变化率很大，在跨距中部附近的变化率较小。

在进行时间序列分析时，常采用移动平均值分析时序数据系列的变化趋势。移动平均值是利用移动平均法根据时间序列，逐项推移，依次计算包含一定项数的序时平均数序列。以移动平均值为基准，应用移动平均法可以求出移动标准差。弓网动态接触压力即是一个时间变量，由于列车运行的时间与位移相对应，所以接触压力可以看作是随接触网位置而变化的参量。因此本文引用移动平均值和移动标准差来描述接触压力的变化。

接触压力移动平均值和移动标准差的计算公式如下：

第n个采样点的移动平均值：

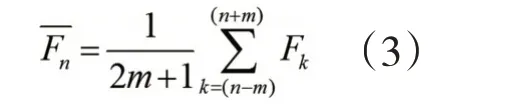
第n个采样点的移动标准差：

式中Fk代表第K个点的接触压力。两公式中的m根据周期按照需要分别取值，本文中F的最小周期取吊弦间距，所以2m取吊弦间距内的采样点数。

根据以上公式，对接触压力进行计算得到的移动平均值和移动标准差曲线与根据欧洲铁路标准EN50318 得到的平均值和标准差曲线分别如图4 所示。

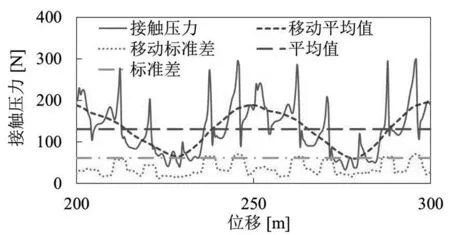
图4 接触压力的变化曲线

从图4中可以看出，移动平均值与平均值相比，能够更好地反应接触压力在一个跨距内的变化情况。标准差表示接触压力相对于平均值的偏离程度，表示接触压力的整体变化程度；而移动标准差表示接触压力相对移动平均值的偏离程度，反应接触压力在吊弦处和吊弦之间的变化程度。引入移动平均值和移动标准差两个指标，能够更直观地表示接触压力随接触网位置的变化。当接触压力移动平均值保持在合理的范围内，移动标准差在跨距内各处值越小时，弓网受流质量越好。

二、线索张力对接触网刚度分布的影响

接触网的刚度分布对是影响弓网受流质量的关键因素之一，在本节的讨论中，主要分析接触线张力和承力索张力变化对接触网刚度的影响。

（一）接触线张力对刚度分布的影响

本节在2.1节模型基础上，将接触线的张力上下变化4kN，即接触线张力为23kN、27kN、31kN。分别对一个跨距长度的进行计算，根据跨距内各点值得到简单链形悬挂接触网的刚度分布曲线分别如图5所示。

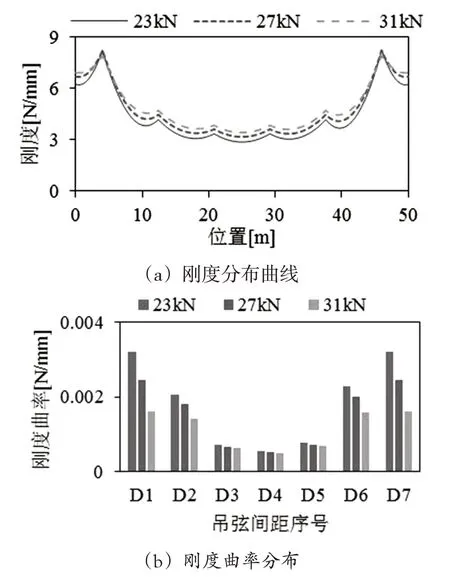
图5 不同接触线张力条件下的刚度分布

从图5（a）中可以看出，接触线张力增加时，跨距内各点值都呈增大的趋势，但是各点的变化幅度与在跨距内所处的位置有关。在简单链形悬挂接触网中，距离定位点最近的首吊弦位置（4m、46m）变化幅度最小，以此为界，随着向跨距中部的移动，变化幅度逐渐增加，跨中的变化幅度最大。

从图5（b）中可以看出，简单链形接触网的曲率在定位点处最大，随着跨距中部的移动，曲率逐渐地减小。随着接触线张力的增大，接触网不同吊弦间距曲率均有减小的趋势，但是，从定位点往跨距中部移动的过程中，减小的幅值逐渐减小，这说明改变接触线的张力，接触网的曲率分布影响较大的是首吊弦位置。而对跨中值的影响比较小。

综上所示，在柔性悬挂接触网中，增加接触线张力有利于增大在跨距之间以及相邻两吊弦之间的变化幅度，同时降低整体的不均匀程度。整体上看，增加接触线张力有利于改善接触网的性能。

（二）承力索张力对刚度分布的影响

本节在2.1节模型基础上，将承力索的张力上下变化4kN，即接触线张力为17kN、21kN、25kN。分别对一个跨距长度的进行计算，根据跨距内各点值得到简单链形悬挂接触网的刚度分布曲线分别如图6所示。

图6 不同承力索张力条件下的刚度分布

从图6（a）可以看出，增加承力索张力时，跨距内各点值均呈增大的趋势，而各点的变化幅度与其在跨距内所处的位置有关。在简单链形悬挂接触网中，从定位点向跨中移动时，变化幅度呈减小的趋势，定位点位置的变化比较明显。

从图6（b）中可以看出，随着承力索张力的增大，接触网不同的吊弦间距中的曲率均有增大的趋势，但是，在简单链形悬挂接触网中，从定位点往跨距中部移动的过程中，降低的幅值逐渐减小。

综上所述，在柔性悬挂接触网中，承力索张力对跨距内各点的均有比较明显的影响。增加承力索张力虽然能增大在跨距之间的变化幅度，但会增加在相邻两吊弦之间的变化幅度，同时会增大的整体大小，增加整体的不均匀程度。从整体上看，增加承力索张力不利于改善接触网的性能。

根据以上分析，接触网线索张力与接触网刚度分布之间的关系是跨距内各处刚度大小与承力索张力和接触线张力成反比，而刚度分布在吊弦处的不平滑程度与承力索张力成正比，与接触线张力成反比。这意味着减小承力索张力和增加接触线张力能使刚度分布曲线在吊弦处变平滑，有利于受电弓的稳定运行。

三、张力对弓网接触压力的影响

（一）接触线张力对弓网接触压力的影响

在2.1节仿真模型的基础上，接触线张力分别为23kN、27kN、31kN、保持其他参数不变，运行速度为300km/h条件下，得到图7所示的弓网接触压力、移动平均值和移动标准差变化曲线。

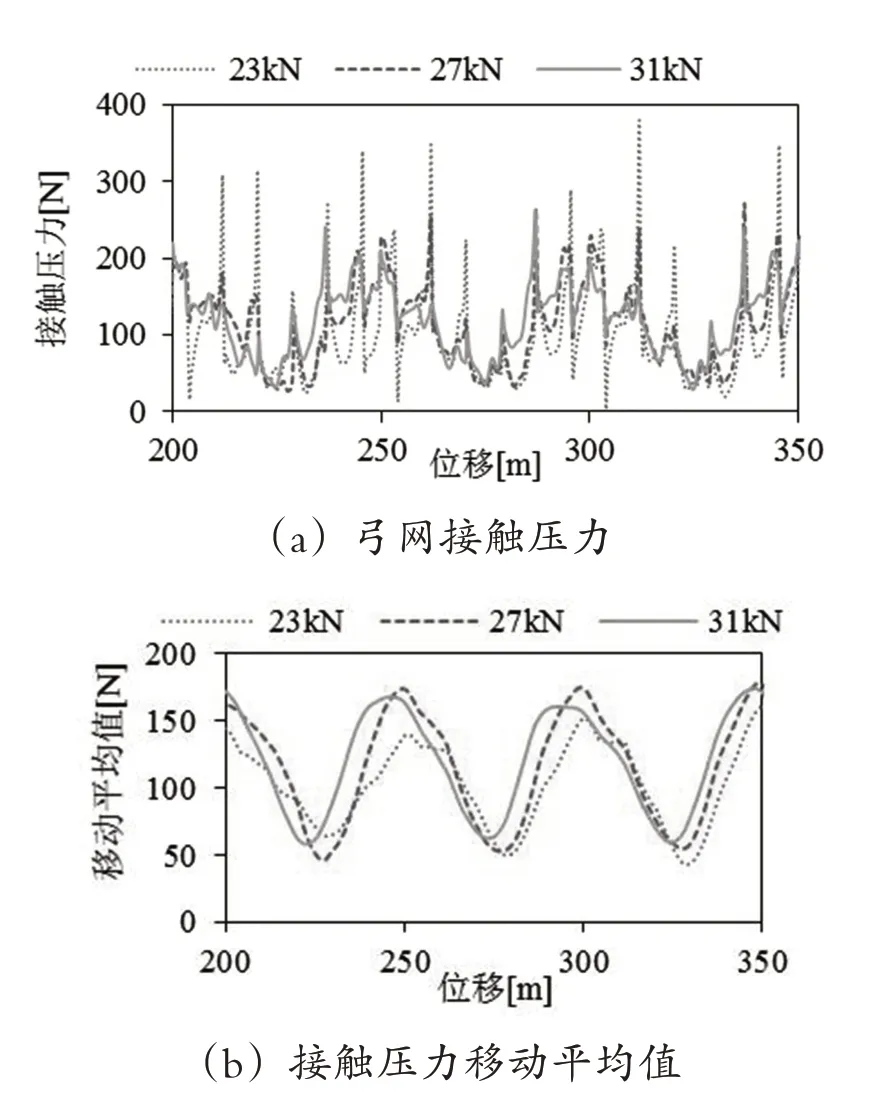
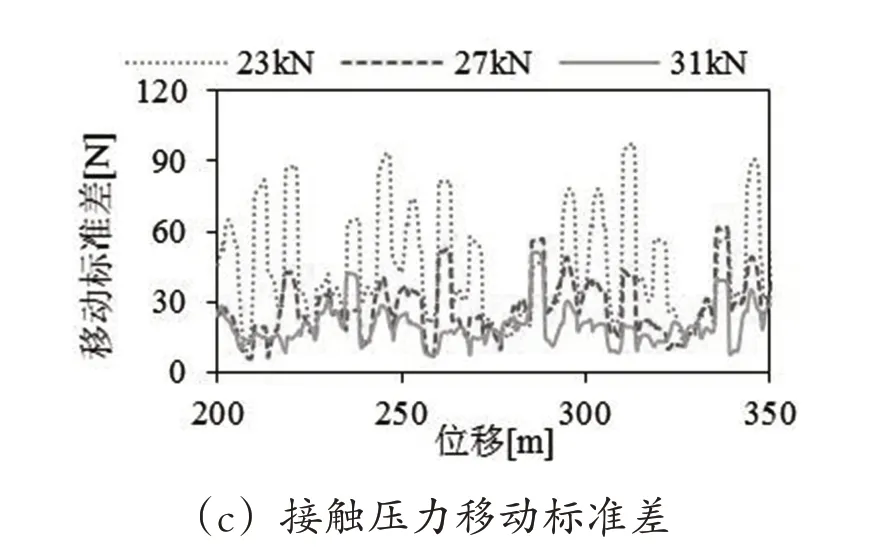
图7 不同接触线张力条件下的弓网接触压力

由图7（a）（b）可知，接触线张力增加时，接触压力呈增加的趋势，原因是接触线张力增加使接触网减小，受电弓抬升起接触线时的平均力会增加。根据图7（a）（c），接触线张力增加时，吊弦处接触压力峰值基本呈下降的趋势，移动标准差呈减小的趋势，这意味着吊弦处接触压力的变化程度降低了，这是因为接触线张力增加后分布曲线在吊弦处的不平滑程度降低，当受电弓经过吊弦时接触压力的变化幅度降低了。

根据以上分析可知，增加接触线张力，接触压力平均大小随的增大而增加，吊弦处接触压力变化幅度随着分布在该处不平滑程度降低而减小。因此，增加接触线张力更有利于弓网受流。

（二）承力索张力对弓网接触压力的影响

以2.1节仿真模型为基础，在承力索张力分别为17kN、21kN、25kN、保持其他参数不变，在运行速度为300km/h 条件下，得到图8 所示的弓网接触压力、移动平均值、移动标准差变化曲线。

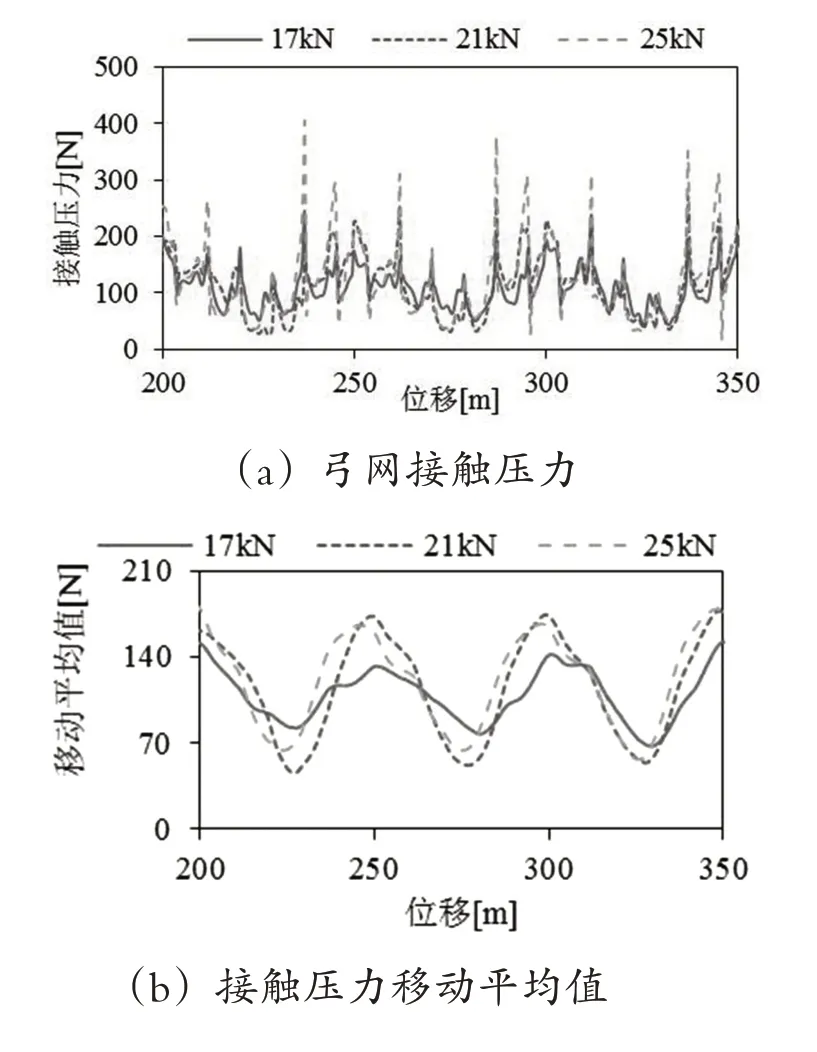
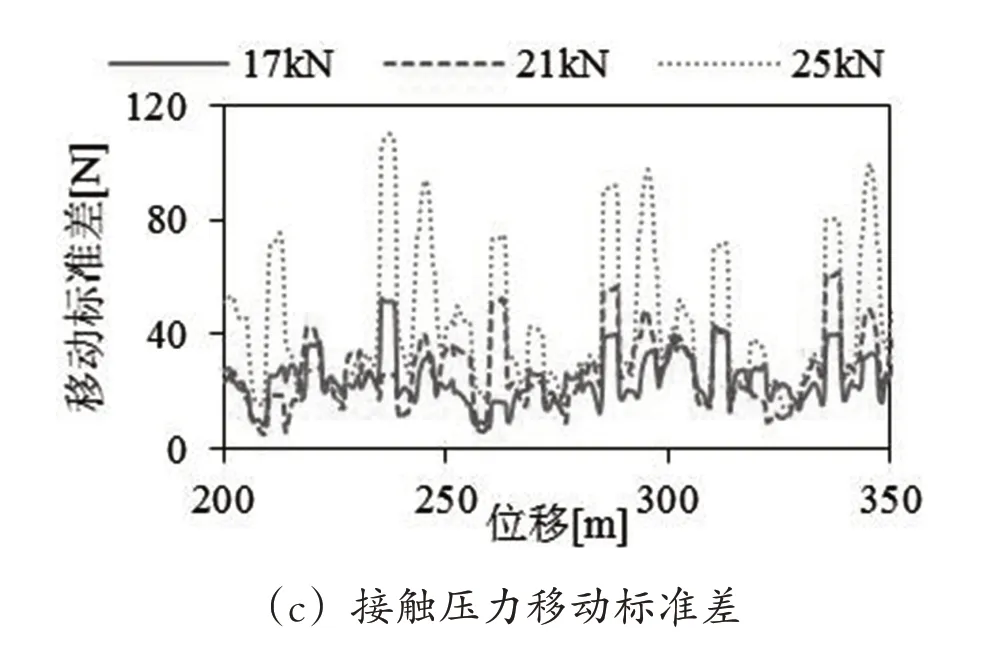
图8 不同承力索张力条件下的弓网接触压力

由图8（a）（b）可知，承力索张力增加时，接触压力呈增大的趋势，移动平均值最低点向跨距中间移动。这是因为承力索张力增加后接触网弹性减小，受电弓在运动过程中抬升接触线的平均力会增加。根据图（a）（c），当承力索张力增加时，吊弦点附近的接触压力尖峰值变大，同时接触压力的移动标准差在吊弦附近呈明显增加的趋势，这说明接触压力在吊弦处的变化幅度增加了。这是因为承力索张力增加后弹性分布曲线在吊弦处的不平滑程度增加，导致了接触压力在吊弦附近的变化幅度增加。

根据以上分析可知，增加承力索张力，接触压力移动平均值随接触网弹性的减小而增加，吊弦处接触压力的变化幅度随着该处弹性不平滑程度的增加而增加。以上结果中接触压力平均值均符合要求，这种情况下，弓网受流质量受接触压力变化程度的影响更大。因此，减小承力索张力对弓网受流更有利。

综上，增加接触线张力或承力索张力，接触网整体增大能使接触压力平均大小增加；增加接触线张力或降低承力索张力，分布曲线在吊弦处不平滑程度减小从而接触压力的变化幅度降低。

四、500km/h 运行速度下的接触网参数优化

在上面的分析中得知，增大接触线张力，减小承力索张力可以有效地改善弓网受流质量。本节将取优化后接触线张力为31kN，承力索张力为17kN，优化前接触网的设计参数与基础模型中接触网设计参数一致。下图9 表示当时速为500kmh 时，优化前后接触压力曲线、接触压力移动平均值、移动标准差和统计值的对比图。

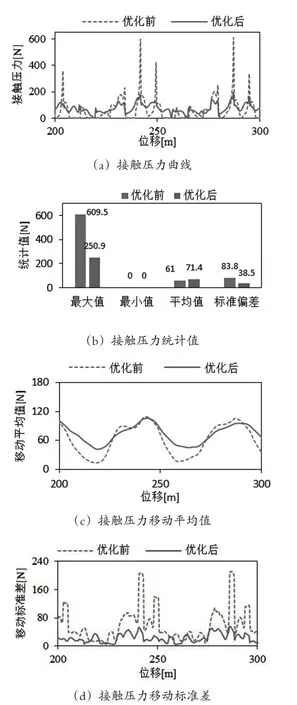
图9 500km/h优化前后接触压力变化

由图9（a）（c）（d）可知，当列车运行速度是500km/h 时，未优化的接触压力曲线在吊弦点处出现了大幅度陡降且发生离线频率高，这是因为当列车速度增大，受电弓的振动加剧，使得弓网耦合系统受流恶化。通过优化后，接触压力曲线明显得到改善，吊弦点处的陡降减小，且离线平率减小。从图9（b）得到，优化前后接触压力从609.5kN 减小到250.9kN，，平均值从61kN 增大到71.4kN，标准偏差从83.8kN减小到38.5kN。

综上所述，通过增大接触线张力，减小承力索张力，有效地降低了列车高速运行时弓网离线率和接触压力幅值骤变的现象，有利于列车高速运行时安全取流。