设计时速120 km线路架空刚性悬挂接触网跨距选择
2017-11-21王洪林
王洪林
设计时速120 km线路架空刚性悬挂接触网跨距选择
王洪林
(中铁第一勘察设计院集团有限公司电化处,710043,西安//工程师)
随着国内城市轨道交通多条线路速度等级达到120 km/h,架空刚性悬挂弓网系统因共振导致受流质量下降的运行区段时有出现,因而架空刚性接触网系统跨距值的设计选用变得相当重要。结合架空刚性接触网模态分析、弓网动态接触压力频谱分析,阐述了设计时速120 km线路架空刚性悬挂接触网跨距选择为8 m的依据。
架空刚性接触网;跨距选择;共振;弓网接触压力频谱分析;模态分析
Π型汇流排和T型汇流排是架空刚性接触网系统中常采用的两种截面形式,由于前者刚度性能好、维修及施工成本低,国内城市轨道交通架空刚性接触网悬挂系统普遍采用Π型汇流排。本文主要研究的是,当列车最高运行速度为120 km/h时,采用Π型汇流排结构的架空刚性接触网跨距的设计选用问题。
1 初定架空刚性接触网跨距
架空刚性悬挂接触网跨距的选择,需根据牵引供电的机械和电气要求,在保证弓网系统滑动接触良好、机车取流连续稳定的基础上确定。如果假定受电弓以匀速运行,根据运行经验,允许接触压力损失不大于其值的12%时,利用梁的动力学微分方程可得架空刚性汇流排布置跨距的理论解为:

式中:
L——架空刚性接触网的跨距;
F——静态接触压力;
E——弹性模量;
I——惯性矩;
p——汇流排单位长度质量;
m——受电弓等效质量;
v——列车匀速运行时的速度。
根据式1计算,按一般情况在不同速度时对应的跨距允许值[1]如表1所示。

表1 列车在不同速度下的刚性悬挂跨距允许值
2 刚性梁波动传播速度与跨距的关系
波动传播速度为单位时间内波沿接触线传播的距离。根据平面简谐波及梁的自由振动方程,推导出刚性梁的波动传播速度公式为:

由式2可知,增大刚性梁抗弯刚度或减小刚性梁的线密度,均可提高刚性梁的波动传播速度。如果增大刚性梁的线密度,虽然可以增大刚性梁的抗弯刚度EI,但也会同时减小刚性梁的波动传播速度,且跨中挠度增大,受流质量会下降,不宜采用;所以一般通过增大刚性梁截面Y向惯性矩I,从而提高其抗弯刚度,进而提高波动传播速度。另外从实际运营知,最高运行速度与波动传播速度的关系一般执行如下经验公式:

式中:
vmax——列车最高运行速度,km/h;
β——无量纲系数,β取值为0.7。
以某城市轨道交通架空刚性悬挂中的汇流排和接触线为例,其Π型汇流排弹性模量E=69 000 MPa,单位长度质量为5.91 kg/m,Y向惯性矩Iy-y=339 cm4;接触线的弹性模量E=120 GPa,单位长度质量为1.35 kg/m。根据以上数据计算得到不同跨距下的波动速度和列车最大允许速度,如表2所示。
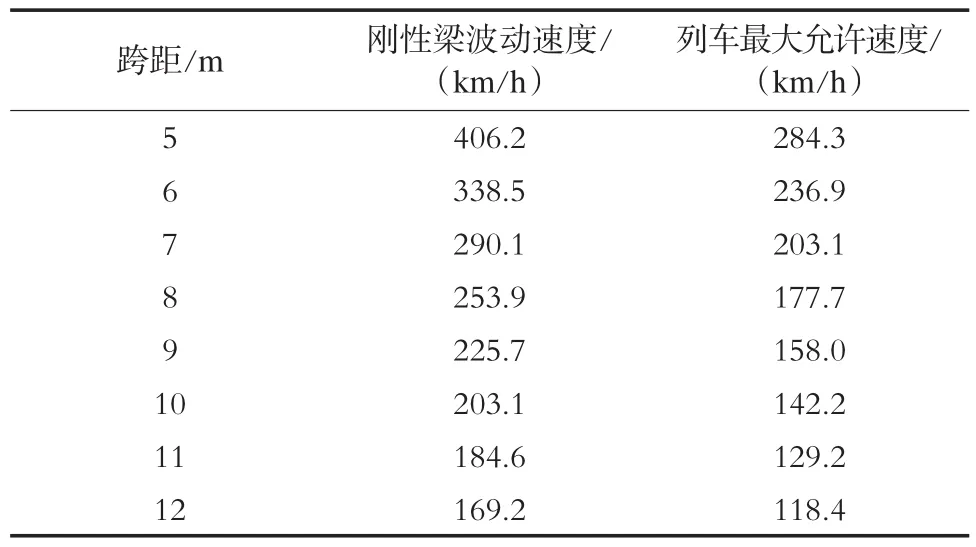
表2 架空刚性悬挂接触网不同跨距下的波动速度与列车最大允许速度
3 不同跨距时刚性悬挂特性的差异
3.1 架空刚性接触网的静力学分析
同样,以上述架空刚性悬挂中的汇流排和接触线为例,汇流排参数:Π型汇流排截面积2 213 mm2,Z向惯性矩Iz-z为113 cm4。接触线参数:线材型号为CTAH150,截面积为150 mm2。根据动能守恒定理,计算出架空刚性悬挂结构的等效刚度keq=3.778 8×107N/m,等效质量meq=2.769 2 kg。在不同的行车速度条件下,刚性悬挂系统跨距值一般可选用6、8、10、12 m。本文主要研究前三种跨距值。
对等跨布置方式进行静力分析,得到不同跨距下刚性接触网的静态挠度(取中间段变形均匀的挠度),刚性接触网跨距为6、8、10 m对应的静态挠度分别为0.79、2.56、6.33 mm。因此,刚性接触的跨距越小,架空刚性悬挂系统的弓网受流质量理论上说应更好。
3.2 架空刚性悬挂接触网的模态分析
振动模态是系统固有的特性,反映系统本身的动力性能。本文运用有限元软件对刚性悬挂接触网结构进行模态分析,主要研究了标准跨距分别为6、8、10 m时,无悬臂等跨距布置、有悬臂不等跨距布置时刚性悬挂接触网共振频率,见表3。
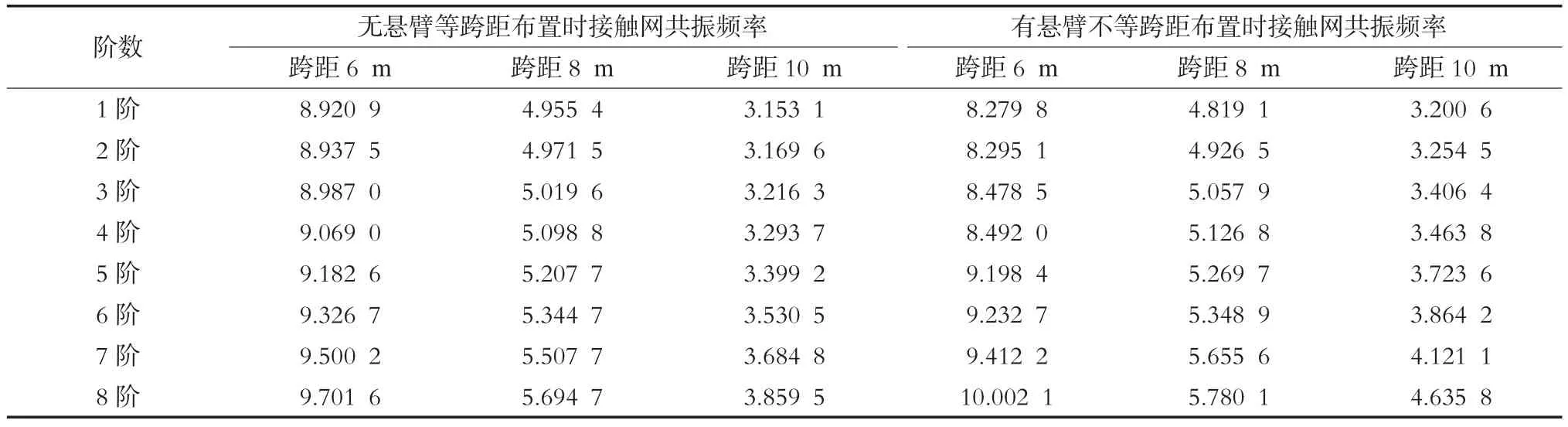
表3 无悬臂等跨距和有悬臂不等跨距布置时不同跨距前8阶固有频率 Hz
刚性接触网跨距为不等跨跨距布置时,锚段中各跨具体参数如表4所示。
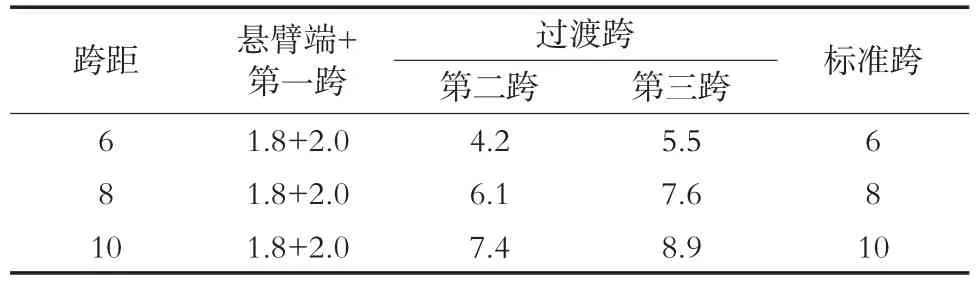
表4 不等跨布置时各跨距设置情况 m
由表3可以看出:跨距越大,刚性悬挂接触网共振频率越小;而同一跨距值,模态阶次越高,共振频率越高。刚性悬挂接触网不等跨布置时的共振频率比等跨距布置时的共振频率略小。因此,实际运营的架空刚性悬挂系统由于锚段关节、道岔定位时要缩小跨距,整个系统的共振频率值会更小。
4 跨距选择对弓网振动的影响
架空刚性接触网跨距的选择应尽量避免其固有频率与受电弓固有频率重合(或接近),以消除共振,同时也要考虑跨距通过频率(列车运行速度除以跨距)基频及倍频的影响。4.1 架空刚性汇流排的振动方程
受电弓以速度v在架空汇流排上匀速运动时,可视为受电弓对架空刚性接触网施以垂向恒力F,并沿汇流排纵向作受迫振动,汇流排为简支梁。则架空刚性接触网的振动公式及受迫振动的动力位移可以表示为:
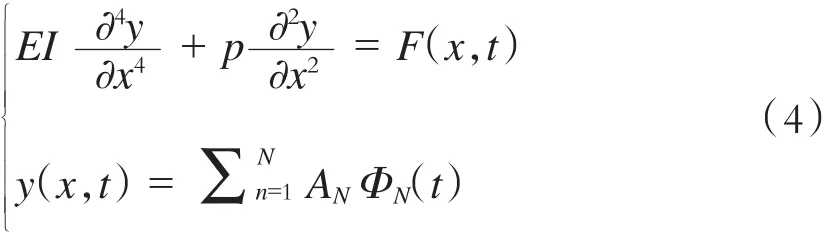
式中
x——架空刚性接触网线路方向位移;
y——受电弓振动纵向位移;
t——受电弓滑行时间;
n——谐波次数;
AN——受变电弓振幅最大值;
ΦN——相位角;
y(x,t)——以x为自变量的时变函数。
利用振型正交性可得解耦后的强迫振动方程为:

式中,ωn为汇流排各阶固有频率,Ωn=pπv/L为移动恒力的广义扰动频率。括号内前项代表强迫振动,后项代表自由振动[3]。可见架空刚性弓网系统为受迫振动系统。
4.2 跨距通过基频
由表5可知,速度恒定时,跨距越大,基频越小;跨距恒定时,速度越大,基频越大。
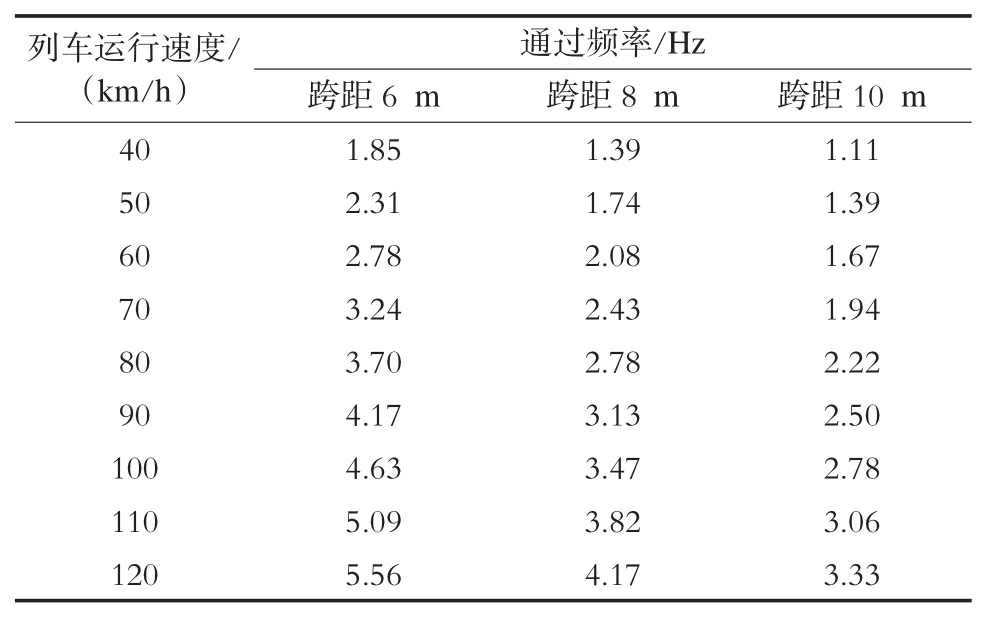
表5 不同列车运行速度、不同跨距的通过频率
4.3 架空刚性弓网系统共振原因分析
一般而言,受电弓前10阶的频率不超过20 Hz,弓网系统是个低频系统。对比表3,不等跨布置时跨距为6 m、8 m、10 m的固有频率均不超过10 Hz。另据文献,广州地铁3号线的受电弓固有频率为5.2 Hz,其北延线的受电弓固有频率约为3.6 Hz。跨距通过基频及其倍频相当于该系统外的激励频率,均可引起受电弓、接触网共振。
从表5可知,不同跨距一定列车速度范围内跨距通过基频范围均有重合,且跨距越小其值越大,但在120 km/h列车运行速度6 m跨距的最大值为5.56 Hz,受电弓固有频率均在0~5.56 Hz范围内。从表3可知,不等跨布置时不同跨距接触网前8阶固有频率均不重合,且跨距越大,其接触网前8阶固有频率越小。跨距越大时接触网固有频率范围越大,与跨距通过基频及其倍频接近的几率越大,从而引发共振。据此,跨距选择时不宜过大。
5 跨距的选择
现对两种不同列车运行速度、不同架空刚性接触网跨距布置的弓网接触压力实测数据进行频谱分析,并截取前20 Hz研究弓网之间的激励频率,统计其接触压力的各项指标。利用弓网接触压力实测数据及弓网仿真数据分析跨距的选择。
5.1 工况1:跨距布置6 m,列车运行速度50 km/h
图1和图2分别是跨距布置6 m、列车运行速度50 km/h的弓网接触压力图和频谱图。采集的数据中列车运行最大速度为61.13 km/h,最小速度为39.55 km/h,平均值为50.17 km/h。跨距通过基频范围在1.83~2.83 Hz之间,与图2中得出的激励频率结果相符合。弓网接触压力最大值为163.129 2 N,最小值为64.375 5 N,平均值为117.503 3 N,方差为12.132 N。
5.2 工况2:跨距布置8 m,列车运行速度90 km/h
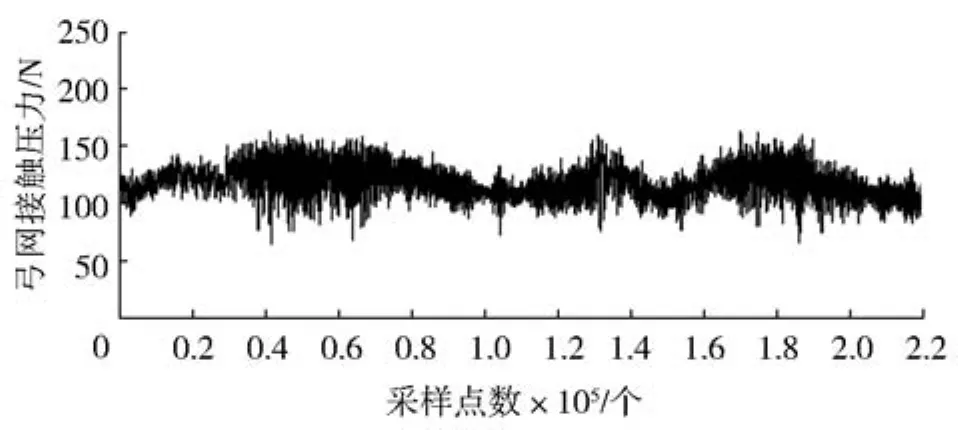
图1 跨距布置6 m、列车运行速度50 km/h弓网接触压力
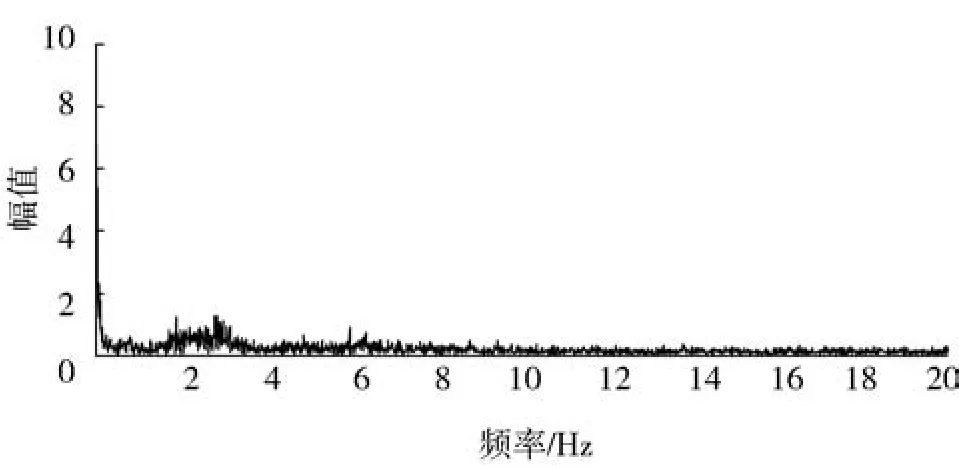
图2 跨距布置6 m、列车运行速度50 km/h弓网接触压力频谱

图3 跨距布置8 m、列车运行速度90 km/h弓网接触压力图
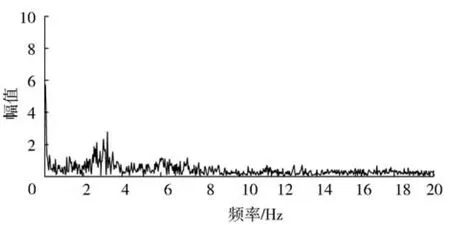
图4 跨距布置8 m、列车运行速度90 km/h弓网接触压力频谱图
图3 和图4分别是跨距布置8 m、列车运行速度90km/h的弓网接触压力图和频谱图。采集的数据中列车运行的最大速度为106.41 km/h,最小速度为70.16 km/h,平均值为89.78 km/h。跨距通过基频范围在2.44~3.69 Hz之间,与图4中得出的激励频率结果相符合。弓网接触压力最大值为129.813 6 N,最小值为21.923 3 N,平均值为111.492 8 N,方差为12.625 9 N。
弓网接触压力的激励频率与跨距通过基频相符合,则已知接触网跨距及列车运行速度时,可得架空刚性弓网系统的激励频率。跨距从6 m增加到8 m,平均运行速度从50 km/h增加到90 km/h,接触压力平均值从117.5 N降至111.5 N,接触压力方差从12.1 N升至12.6 N;这说明后者弓网动态特性较好,只要弓网系统匹配合适,增大跨距,提高列车运行速度,不一定就会引起弓网受流质量变坏。
5.3 工况3:车速相同,跨距变化
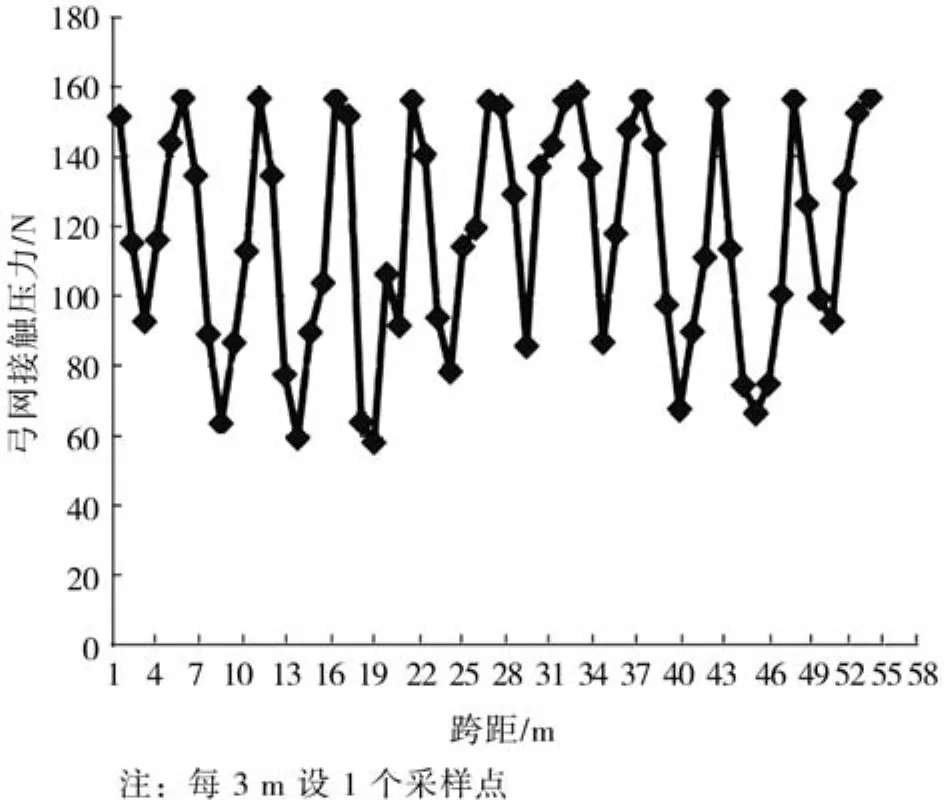
图5 跨距6 m、车速120 km/h弓网接触压力图
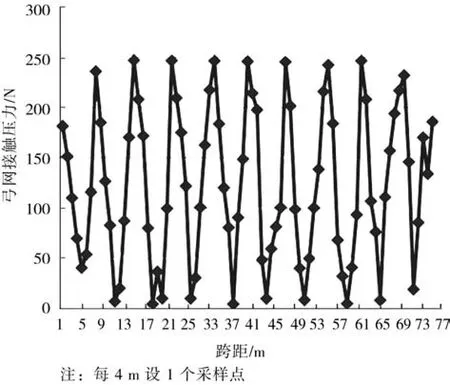
图6 跨距8 m、车速120 km/h弓网接触压力
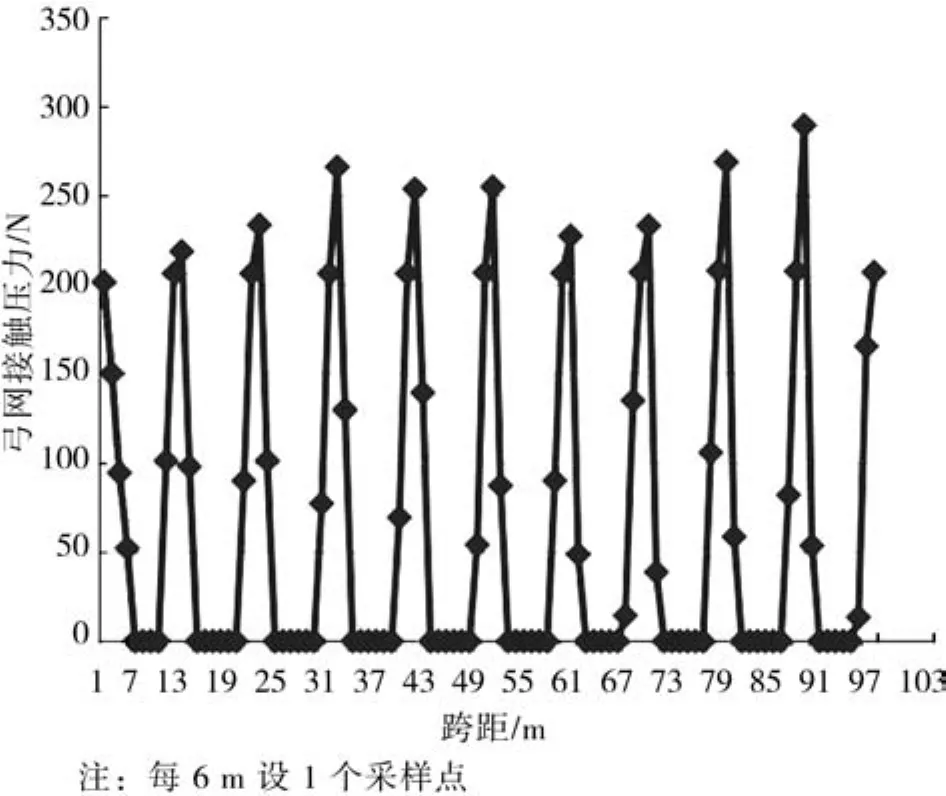
图7 跨距10 m、车速120 km/h弓网接触压力
分析架空刚性悬挂弓网动态特性时,主要基于弓网相互作用时的动态接触压力。图5至图7为相同车速、不同跨距布置时弓网接触压力值。从图中可以看出,跨距越大,弓网接触压力越离散;跨距10 m时,弓网接触压力出现零值的现象加大,此时弓网动态特性明显下降。图7表明,车速运行在120 km/h时,跨距不宜布置为10 m。另外,对比图5至图7表明,车速运行在120 km/h时,6 m跨距布置时弓网动态特性最好,但综合经济技术两方面考虑,车速运行在在120 km/h时,8 m跨距布置最可行。
5.4 工况4:跨距相同,车速变化时弓网仿真接触压力统计分析
接触网跨距为8 m,受电弓静态抬升力选定为120 N,列车运行速度分别为80 km/h、100 km/h、120 km/h时的弓网接触压力见图8、图9及图6,相关统计值见表6。
速度为80 km/h时,弓网配合良好;随着速度的提高,速度为120 km/h时,弓网配合比速度为80 km/h的要差,但总体而言弓网动态相互作用仍安全可控。
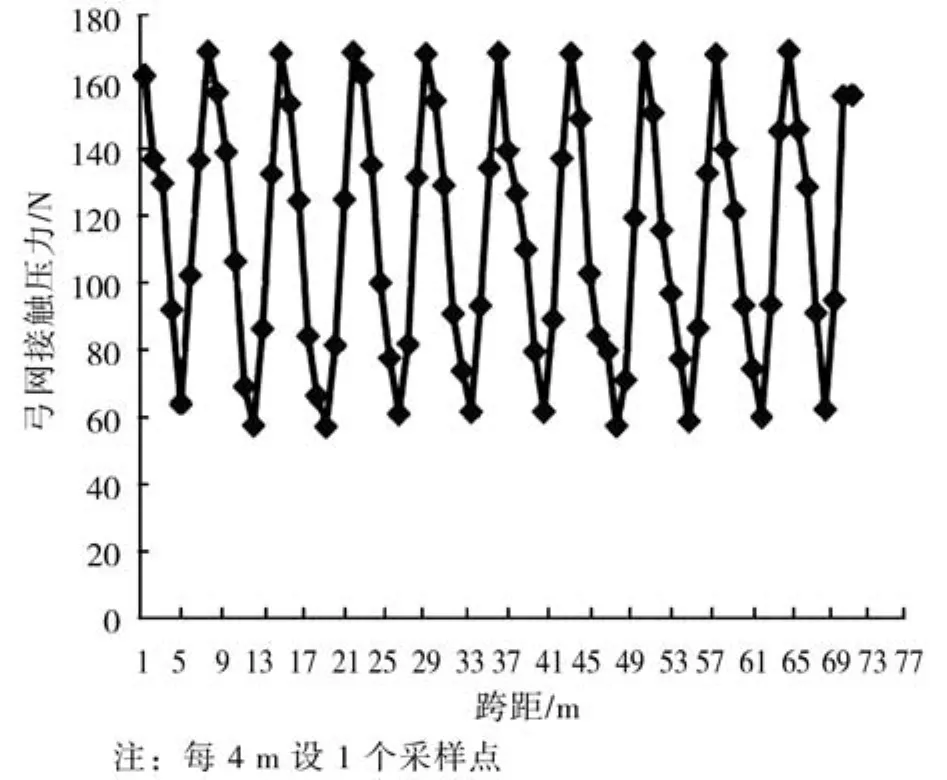
图8 跨距8 m、车速80 km/h弓网接触压力

图9 跨距8m、车速100 km/h弓网接触压力
从表6同样可以看出,随着列车速度的增加,接触压力的均值、标准差和变化幅值都变大,弓网动态特性越来越差。跨距为8 m时,列车速度值在120 km/h弓网动态接触压力最小值仍大于零。同前所述,8 m跨距布置、车速运行在120 km/h时技术安全上是可行的,经济性能是最优的。
6 结论
本文首先从梁的动力学微分方程得到架空刚性悬挂跨距的理论解,并通过分析刚性梁波动传播速度与跨距的关系,初步确定列车运行速度为120 km/h时,架空刚性接触网跨距值采用8 m是适宜的。随后,利用静力学分析及模态分析得出架空刚性接触网不同跨距的前8阶固有频率,引入弓网实测接触压力的频谱分析,结合跨距通过基频和弓网仿真接触压力统计值,研究了不同跨距时刚性悬挂弓网系统的动态特性,得出如下结论:①跨距通过基频及其倍频相当于该系统外的激励频率,均可引起受电弓、接触网共振;从防止弓网共振的角度看,跨距选择不宜过大。②弓网接触压力的激励频率与跨距通过基频相符,如果弓网系统匹配合适,增大跨距,提高列车运行速度,弓网动态特性仍保持良好。③跨距为8 m、列车速度值在120 km/h时弓网系统仍未发生离线,说明从技术安全上是可行的;另外,车速为120 km/h时,相较于6 m跨距布置而言,采用8 m跨距布置从经济方面考虑是最优的。因此,时速120 km/h时架空刚性接触网宜采用8 m跨距值。
[1] 杨理兵.π型架空刚性接触网技术研究[J].城市轨道交通研究,2006(11):50-53.
[2] 尹魁元.接触网刚性悬挂跨距的选择[J].都市快轨交通,2013(8):105-108.
[3] KIESSLING,PUSCHMANN,SCHMIEDER.电气化铁道接触网规划设计施工[M].北京:中国电力出版社,2004,338-339.
[4] 马果垒.受电弓系统研究[D].成都:西南交通大学,2009.
[5] 关金发,吴积钦,方岩.刚性接触网的研究综述及展望[J].都市快轨交通,2016,29(6):37-43.
[6] 李军,汪波,郑玄,等.刚性供电网条件下120 km/h地铁受电弓弓网动态匹配问题[J].机车电传动,2014(1):80-83.
Selection of Overhead Rigid Catenary Span on the Designed 120 km/h Line
WANG Honglin
Many urban rail transit lines in China have achieved the speed of 120 km/h,resulting in current quality decrease of the overhead rigid catenary system because of the sympathetic vibration.Therefore,the selection of overhead rigid catenary span becomes very important in the design.Combined with analysis of the overhead rigid catenary modal and the catenary contact force spectrum,the basis for 8m overhead rigid catenary span on the designed 120 km/h line is elaborated.
overhead rigid catenary; span selection;sympathetic vibration; analysis of catenary contact force spectrum;modal analysis
U225.1
10.16037/j.1007-869x.2017.10.017
Author′s address China Railway First Survey and Design Institute Group Co.,Ltd.,710043,Xi'an,China
2017-05-16)