高等数学中收敛数列及函数极限性质的教学探讨

（周口师范学院，河南周口466000）

掌握数列及函数极限的概念和性质是学习后续内容的基石。但是对于高等数学的初学者来说，数列及函数极限涉及的ε-Nε-δ和语言理解起来存在一定困难，尤其是对于基础较差的学生，很不理解ε、δ、N 在解决问题中的取法。为了让学生掌握极限的内涵，许多学者对极限的教学方法进行了探讨。文献中探讨了借助实例和几何图形来论述数列极限的定义的方法，以期达到让学生加深对极限概念理解的目的。文献对极限教学的有效策略进行探讨，主要论述了教学中采用极限理论的解题方法，以期为相关的实践提供理论参考。文献探讨了根据微积分的发展史和极限中体现的哲学思想等科学思想对极限的教学进行设计，让学生通过感性认识到理性认识的过程理解极限中的重要思想，体会极限过程中的量变到质变、无限和有限的辩证关系。

一、极限性质教学的不良现象

极限在高数的学习中占有极其重要的地位，本应该让学生尽量理解透彻，但是某些老师在授课中缺乏这种意识，对极限概念及性质的讲解存在随意现象，主要表现在以下两个方面。

（一）过分依赖PPT 课件。多媒体辅助教学已在高校普遍盛行，由于其视觉效果、前后回顾方便等多种优点，受到大多数老师及学生的喜爱。但是多媒体教学还不能完全取代传统的教学模式，尤其是理工科的教学，因为理工科有其自身的特点，很多公式定理需要详细推导证明，只让学生观看PPT课件很难达到让学生理解的效果，导致学生对极限性质及证明的关键点不能理解。

（二）答疑不科学。答疑是教学中的一个重要环节，但是部分教师对学生提出的问题回答得很不科学。这可能与教师的专业水平、研究方向有一定关系。比如在经典高等数学教材（高等数学第七版上册，同济大学数学系编，高等教育出版社）收敛数列的性质一节中，定理1（极限的唯一性）证明中“神秘”的出现了“取”，很多学生存在疑问：为什么取？怎么取得呢？有没有其它值可取？当学生带着这些问题问老师的时候，有些老师不假思索地回答说是根据经验取得的，或者有些老师解释说根据极限的定义，这样取可以达到证明的目的。显然，这些回答并没有解决学生的疑惑。

二、极限性质的教学探讨

（一）重视传统教学方式。传统的板书教学形式具有很强的灵活互动性，由于其朴素而简便的板书手段对教师的教学行为束缚小，教师可根据课堂教学的实际需要，及时调整自己原有的课前预设方案。而多媒体教学是以流线型特征展现的，它在学生思考体会与笔记记录、教师点拨与学生回味等方面都存在着明显的弱点。因此在授课中不能过分依赖于PPT 课件，要重视板书教学，将极限的性质定理在黑板上给学生详细推导证明，不仅有利于学生理解，而且可以加深学生对知识的印象，即板书可以有效促进学生对知识的理解记忆。

（二）刨根问底，探究实质。如何解答学生存在的疑问：为什么取？怎么取的呢？有没有其它值可取？当然这需要老师认真备课，对知识点要理解的透彻。下面我们以收敛数列的唯一性定理和函数极限的局部保号性定理为例，揭开ε 取值的神秘面纱。

定理1（极限的唯一性）如果数列收敛，那么它的极限唯一。

先看教材中的证明过程。

证用反证法。假设同时有xn→a 及xn→b，且a＜b。取。因为，故正整数N1，当n＞N1时，不等式

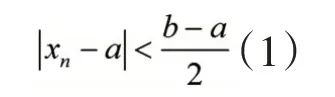
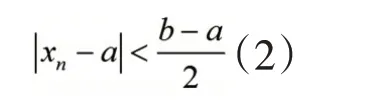
都成立。取N=max｛N1，N2｝，则当n＞N时，（1）式及（2）式会同时成立，但由（1）式有，由（2）式有，这是不可能的。这矛盾证明了本定理的断言。

假设同时有xn→a及xn→b，且a＜b，由极限的定义知对ε ＞0，存在正整数N，当n＞N 时有同 时 成 立 。 根 据，又根据，即当n＞N 时，xn落在了两个区间（a-ε，a+ε）和（b-ε，b+ε），由a＜b，这两个区间的示意图有以下3种情况：

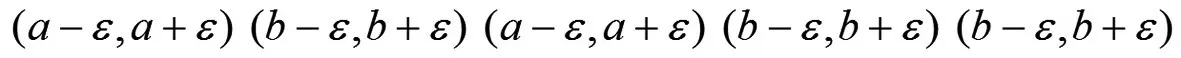
由图可知，要想得出矛盾，只需使两个区间没有交集就可，也就是说ε 的取值只要满足情况1和情况2都可以得出矛盾，完成定理的证明，即只要取ε满足不等式a+ε≤b-ε即可，解不等式得。因此，在本定理的证明中取，仅仅是一个临界值，可以取的任何值来完成定理的证明。

先看教材中的证明过程。

证就A＞0的情形证明。

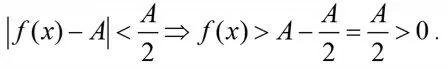
类似地可以证明A＜0的情形。

三、结束语

根据学科的特点及目前部分老师在授课中存在的不足，本文对极限性质的有效学习进行了探讨：（1）重视板书授课方式，尽量把关键点给学生演示清楚；（2）认真对待答疑，不要评想当然，或敷衍了事；（3）刨根究底，探究实质。对极限性质的证明中的“神秘”取值要给学生讲透彻，揭开它的神秘面纱，澄清其取值的实质，让学生不再困惑。