求解张量分裂可行问题的半定松弛法
2020-12-27金雨轩徐旭冬赵金玲
金雨轩,徐旭冬,赵金玲
(北京科技大学 数理学院,北京 100083)
0 引言
本文研究张量分裂可行问题,即求一个向量x,使得
x∈C并且Axm-1∈Q,
(1)
其中:C⊆Rn,Q⊆Rp,Rn和Rp分别代表n维和p维欧氏空间。A是m阶p×n×…×n维张量,即张量A=(ai1i2…im),其中,i1= 1,…,p;ij= 1,…,n(j= 2,…,m)。
张量分裂可行问题可以视为分裂可行问题的一种推广。分裂可行问题广泛应用于图像重建、信号处理等领域中[1-2]。这一模型最早由文献[3]提出,问题描述为:求一个向量x,使得
x∈C,Ax∈Q,
其中:A为矩阵。后来,分裂可行问题被文献[4]进一步推广为多集分裂可行问题。
CQ算法是求解分裂可行问题的经典算法,其他求解分裂可行问题和多集分裂可行问题的方法,都可以看作是CQ算法的变形。至今已有许多学者对CQ算法进行了研究和改进[5-12]。但是,CQ算法主要应用于问题中A是矩阵的形式,并且由于CQ算法需要矩阵A的特征值,而张量的特征值与矩阵不同,所以尚无法直接应用于张量分裂可行问题。而且,CQ算法的计算效率依赖于初始点x0和参数γ的选择。
近期,文献[13]提高了求解多集分裂可行问题的效率,文献[14]利用牛顿投影法求解分裂可行问题,文献[15]研究了求解特定Banach空间中的多集分裂可行问题,但是对于张量分裂可行问题的研究较少。
半定规划是线性规划的推广,许多凸规划问题都可以转化为半定规划问题。文献[16-18]提出了用矩阵不等式表示半代数集合,即一种由多项式不等式定义的集合。文献[19]通过moment松弛法,将A为矩阵的分裂可行问题转化为半定规划问题来求解,并证明了相关理论。这一方法对于集合C和Q非凸的情况也很有效。本文受到这一思路的启发,将张量分裂可行问题转化为半定规划问题来求解。
本文主要研究由多项式定义集合的张量分裂可行问题,即式(1)中的集合C和Q由多项式给出,如下所示:
C={x∈Rn|f(x)≥0},Q={y∈Rm|g(y)≥0}。
将张量分裂可行问题转化为半定规划问题,即将式(1)转化为多项式f(x)≥0,h(x)≥0,通过松弛的方法将问题映射到更高维度的空间中,求得高维空间中的解,再将解通过投影的方式映射回低维空间,最后判断是否能求出可行解。
1 半正定松弛原理
1.1 预备知识
设A是m阶n维张量,则A包括nm个元素:
A=(ai1i2…im),ai1i2…im∈R,
其中:ij=1,2,…,n,j=1,2,…,m,当m=2时,张量即变成n×n维方阵。本文所研究问题中的张量并非“方”的,其中m阶张量A的维数是p×n×…×n。
当向量x=[x1,x2,…,xn]T,张量向量乘法为:
所得到的Axm-1是p维向量,Axm-2是p×n阶矩阵,Ax是m-1阶张量,维数变为p×n×…×n(少一层)。
1.2 分裂可行问题转化为半定规划问题
张量分裂可行问题欲求一点x,满足
x∈C并且Axm-1∈Q。
A是m阶张量,维数为p×n×…×n。 集合C和Q由多项式不等式给出:
C={x∈Rn|f(x)≥0},Q={y∈Rm|g(y)≥0},
(2)
将Axm-1代入g(y),得到集合W:
Axm-1=[y1,y2,…,yp]T,w(x):=g(Axm-1);
W={x∈Rn|w(x)≥0}。
张量的分裂可行问题就等价于找到一点x,并且满足
x*∈C∩W={x∈Rn|f(x)≥0,w(x)≥0}。
(3)

(4)
由此,将张量分裂可行问题转化为半定规划问题(4),并且给出了相应的目标函数和约束条件。
1.3 localizing矩阵
其中:Fα为对称矩阵。
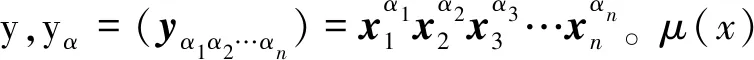
(5)
易知,y0=1。

(6)
(7)
1.4 松弛化原理
半定规划原问题为:
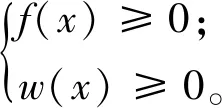
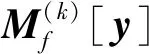
(8)
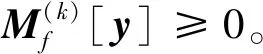
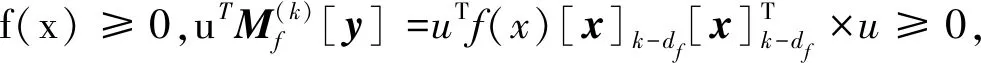
定理2若x*∈C∩W,则x*∈Hk。Hk为C∩W的松弛化集合的投影。

C∩W={x|f(x)≥0,w(x)≥0} 。
C∩W总是包含在集合Hk中,s=max 「def(f)/2⎤,「def(w)/2⎤,对于所有k≥s,每个Hk是C∩W的半定松弛后的集合,并且C∩W⊆Hk,包含以下嵌套关系:
Hs⊇Hs+1⊇…⊇C∩W。
令y=[x]2k,将式(4)映射到高维空间中,即得到k阶Lasserre moment松弛(式8),利用半定规划松弛法求y,得到最终的x*。最后判断,若x*∈C,Axm-1∈Q,则得到张量分裂可行问题(1)的解。
1.5 算法步骤
集合C和Q都可化为多项式的形式,令k=d。
步骤Ⅰ 将张量分裂可行问题通过moment松弛法转化为半定规划问题(4)。
步骤Ⅱ 求解半定规划松弛化问题,若可以得到可行解y*,则进入步骤Ⅲ,若没有y*符合该半定规划问题,则停止计算。
步骤Ⅲy*投影到Rn中,得到最终的x*,判断若x*∈C,Axm-1∈Q,则得到张量分裂可行问题(1)的解。若不成立,k=k+1,返回步骤Ⅱ。
2 数值实验
本节主要介绍利用半定松弛法求解张量分裂可行问题的数值实验结果。所有数值计算均应用于处理器为 Intel(R)Core(TM)i7-7500U CPU(2.70 GHz)的笔记本电脑上,所使用的软件版本为MATLAB r2016a。主要利用了GloptiPoly[20]、SeDuMi[21]和张量工具箱[22]求解半定规划松弛。
例1求向量x,使得x∈C并且Axm-1∈Q。C和Q定义为:
其中:集合C为球体;r1为该球体的半径;100代表各分量值都为100的向量。A为4阶张量,维数为3×2×2×2,Aijkl=0.015i+0.01(j+k+l),共有24个元素,展开形式如下所示:

将维数为3×2×2×2的张量A与未知量x=[x1,x2]相乘,得到3维向量Axm-1:
将C和Q化简为式f(x)和w(x),再将Axm-1代入g(y)求得w(x):
g(y):=(y1-100)2+(y2-100)2+(y3-100)2≤4 900;
利用半定松弛法求解例1,改变r1的大小时,求解结果如表1所示。

表1 例1的求解结果
本例主要探究了r1的改变对于该算法有何影响以及是否稳定。结果表明:随着r1的不断增大,半定松弛算法所花费的时间相差不大,但是迭代次数有小幅上升。当r1=5时,可行的解距离f(x)的边界较近,出现了没有计算出可行解的情况。 但是当r1不断增大时,可行解距离f(x)的边界较远时,计算情况较好。
例2张量分裂可行问题中C和Q与例1一致,取r1=10,考虑张量A的大小对于算法的影响,当i=j=k=l=1时,A1111=a(0.015i+0.01(j+k+l))。 其他情况时,Aijkl=0.015i+0.01(j+k+l)。根据A计算得出相应的Axm-1、f(x)和w(x),再利用半定松弛法求解。改变a的大小时,求解结果如表2所示。

表2 例2的求解结果
本例主要探究了张量中某个值的改变对于该算法有何影响以及是否稳定。 结果表明:花费的时间与张量A的数值相差不大。 并且由A1111是与x1相乘可以看出,随着a的增大,w(x)中x1的系数不断增大,导致解x*中的x1不断缩小,x2不断增大。
例3张量分裂可行问题(1)中C和Q定义为:
Aijkl=0.015i+0.01(j+k+l),(1≤i≤5,1≤j,k,l≤4);
其中:A为4阶张量,维数为5×4×4×4,共有320个元素,与前2个例子相比,维数有所增加;100代表各分量值都为100的向量。
根据A计算得出相应的Axm-1、f(x)和w(x),再利用半定松弛法求f(x)和w(x)的解,求解结果如表3所示。

表3 例3和例4的求解结果
本例主要探究了张量A的维数与算法之间的关系。与例1相比,张量维数由3×2×2×2维增加到5×4×4×4维,元素个数由24个增加到320个,变量的个数也由2个变为4个。随着变量个数的增加,计算时间和迭代次数都有所增加,但是该算法依然可以得出结果。
例4A为6阶张量,维数为3×2×2×2×2×2,共有96个元素,Aijkloq=0.015i+0.01(j+k+l+o+q)(0≤i≤3,0≤j,k,l,o,q≤2)。为了确保有解,C和Q定义为:
其中:200代表各分量值都为200的向量。
根据A计算得出相应的Axm-1、f(x)和w(x),再利用半定松弛法求f(x)和w(x)的解,求解结果如表3所示。
本例主要探究了张量A的阶数与算法之间的关系。与例1相比,张量阶数由4阶增加到6阶,计算时间和迭代次数都相差不大,该算法依然可以计算出可行解。
3 结论
本文提出用半定松弛法解决张量分裂可行问题,将张量分裂可行问题转化为半定规划问题,再利用半定松弛的算法求解,并且给出了半定松弛法的收敛性证明。对于集合C取不同范围、张量A取不同值、张量A取不同维数和张量A取不同阶数的情况都进行了数值实验,本文算法均可以计算出可行解,验证了算法的可行性和有效性。
