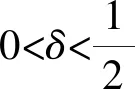外域上耦合波动方程组的局部能量衰减
2020-12-27武洁琼吴江涛
武洁琼,吴江涛
(山西大学 数学科学学院, 山西 太原 030006)
0 引言
设V是RN中的紧集,V关于原点是星形的,Ω=RNV。研究如下带有局部耗散的耦合波动方程组初边值问题的局部能量衰减:
(1)

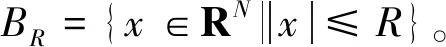
文献[1-13]均是考虑方程主部是常系数的情形。当主部是变系数,即用divA(x)▽u取代△u时,问题更加复杂。文献[14-15]借助黎曼几何方法,分别研究了变系数主部情形下,带线性局部阻尼的波动方程的柯西问题和外域上带半线性局部阻尼的波动系统的能量衰减性质。
注意到文献[1-15]均研究单个波动系统的能量衰减性质。然而,耦合是工程实践中的一种普遍现象,而且有界域上耦合波动方程组解的能量衰减已得到了充分的研究。例如,文献[16]研究了当问题(1)内部没有阻尼(a(x)≡0)时,通过边界阻尼所引起的能量指数衰减的性质,文献[17]则研究了通过速度耦合的波动方程的衰减性质。
本文考虑外域上通过位移耦合的波动方程组的局部能量衰减问题。假设两个波动系统在边界的一个邻域上耦合,系统的阻尼只在一个有界区域施加。利用乘子法,结合加权函数方法及截断技巧,得到耦合系统局部能量的多项式衰减估计。
关于局部阻尼和耦合区域做如下假设:

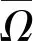
1 主要结论
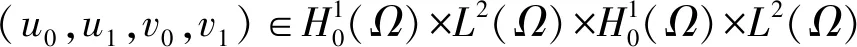
那么,问题(1)的解(u,v)有局部能量衰减,即对任意的R>L,有:
ER(t)≤CI0(t-R)2δ-1,

2 定理1的证明
采用乘子法可得到以下基本不等式。在问题(1)的第1个方程两边分别乘以ut,tut,x·▽u,u,并在(t0,t)×Ω上积分;在问题(1)的第2个方程两边分别乘以vt,tvt,x·▽v,v,并在(t0,t)×Ω上积分,得到:
(2)
(3)
(4)
其中:η(x)是Ω的边界上x处的单位外法向量,
(5)
(6)
下面估计式(6)的各项。注意到V关于原点是星形的,有:
(7)
|(x·▽u(t),ut(t))+(x·▽v(t),vt(t))|≤
(|▽u|2+|ut|2+|▽v|2+|vt|2)dx+
(8)
用Young不等式,并注意到suppa(·)⊂BL,对式(6)左边倒数第2项有以下估计:
(9)
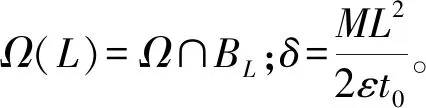
注意到两个系统在边界的一个邻域上耦合,对式(6)左边最后一项有如下估计:
(10)
结合式(6)~式(10),得到:
(11)
由式(8)知:|(x·▽u(t0),ut(t0))+(x·▽v(t0),vt(t0))|≤C(R,t0)I0,于是
(12)
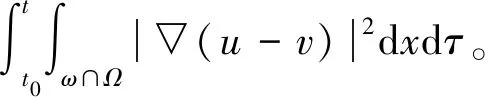
(13)
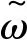
在方程组(13)的第1个方程两边乘以ξφ得:
(14)
注意到
从式(14)得到:
(15)
注意到Eφ(0)≤CI0,从式(11)、式(12)和式(15)得到:
(16)
由于suppa(·)⊂BL={x∈RN||x|≤L},由Poincare不等式,并注意到系统的能量衰减,得到:
(17)
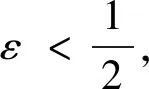
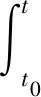
(18)
接下来估计式(18)右边第3项,有以下引理。
引理1存在与u,v无关的T0>0,C>0,使得当T>T0时,有:
证明采用反证法。记φ=u-v,假设结论不成立,则存在序列tn,φn使得:
(19)
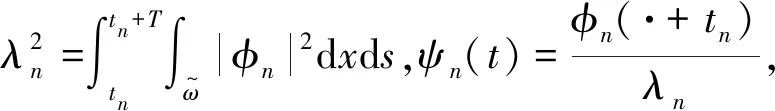

ψtt-△ψ+2α(x)ψ=0,
(20)
现在将引理1中得到的不等式代入到式(18),当t-t0>T0时,有:
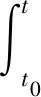
(21)
为了控制式(21)右边最后一项,引入加权函数φ(x,t)=|x|-t,类似于文献[4]的引理2,有如下引理。
引理2令φ(x,t)=|x|-t,对于问题(1)的解(u,v),有如下不等式成立:
于是式(16)成为:
(22)
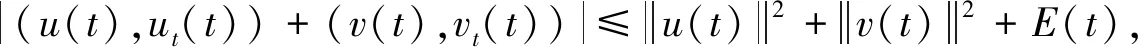
引理3设u0+u1∈L2N/(N+2),v0+v1∈L2N/(N+2),那么:
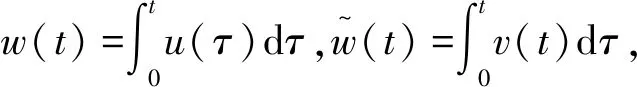
对电子14级、15级的学生,在编写或者挑选教材时,编程语言以C语言为主,易读、好维护、可移植性好,编译效率高。内容编排采用项目教学法,每个学生有一个和教材配套的开发系统,教学做和仿真结合。在教学过程中将Keil和Proteus引入课题,构建虚拟的单片机实验室,先仿真,然后在单片机系统上进行实物练习。有过程,有现象,有结果,学完之后至少能对本门课程入门了。通过改革,学生的学习兴趣有了极大的提高。
(23)
式(23)的第1个方程两边同乘wt,并在Ω×(0,t)上积分得:
(24)
(25)
由Hölder不等式、Sobolev嵌入定理及Young不等式有:
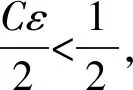
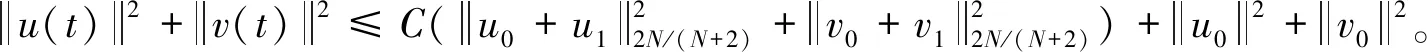
现在回到定理1的证明。由式(22)和引理2,得到:
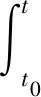
(26)
接下来利用积分因子(t-R)-2δ-1乘以式(26)得:
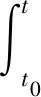
即
对上式在(t0,t)上积分得:
所以
(27)
将式(27)代入式(26)得:
ER(t)≤CI0(t0-R)-2δ(t-R)2δ-1,