基于格网划分的道路最近邻查询算法

闫红松，George Almpanidis，凡高娟

(河南大学 计算机与信息工程学院，河南 开封 475003)

0 引言

目前，地图服务已经成为人类衣食住行必不可少的方式，在地图服务中，查询最近设施(例如，饭店、学校等)是最为普遍的，最近邻查询算法是其中最常用的算法。虽然目前的最近邻查询算法众多且比较成熟，但是仍然面临着巨大的挑战。例如，现实中的物体数量远远大于被查询的最近邻设备数量；另外，真实的物体不仅与其自身的地理位置有关，还与其周围复杂的地形以及路线有很大关系。这些因素都会增加对最近邻物体查询的难度。

为了解决现实问题，有许多成熟的最近邻算法，例如文献[1]中的聚合关键字最近邻(aggregate keyword nearest neighbor,ANN)算法,其基本思想是Dijkstra算法，以欧几里得距离的形式计算最短路径距离；文献[1]中的增量网络扩张(incremental network expansion,INE)算法，是从Dijkstra算法派生出来的，记录了当前处理过的优先级较高的一些顶点，也就是保存了到查询点最近的点的集合。文献[2]使用空间诱导连锁认知(spatially induced linkage cognizance,SILC)索引法解决K近邻(K-nearest neighbor,KNN)查询。在文献[3]中,INE算法的搜索空间可能十分巨大，而路由转换和关联目录(route overlay and association directory，ROAD)算法通过排除不包含目标区域的搜索剪枝对INE算法进行了优化。文献[4]同样是以图的划分构造一棵树的索引，从而通过子图层次来高效计算道路网络之间的距离。这种划分和ROAD算法中的划分相似，通过递归按层次不断划分。与ROAD算法划分不同的是，G-tree算法的每次划分，每个点都属于不同的区域，不存在交叉。文献[5]更为详细地描述了文献[1-4]算法的效率分析。目前，最近邻查询也有通过对查询区域进行划分的算法，例如，文献[6]将查询区域进行格网划分。然而，现有的最近邻算法都是把数据点和道路视为顶点和边的网络图[7]，这与现实生活并不完全一致，事实上，更多的物体是在道路内，也就是点在边上，而非只是在边的端点。另一方面，现有最近邻算法并没有给出查询点所在位置的具体算法，而是以顶点出发计算其最近邻的点集合[8-16]。

针对以上问题，本文结合INE算法[1]，设计了一种基于格网划分的算法，将查询区域进行N×N的方格划分，并且根据物体与道路真实的包含关系进行结构设计。这样可以到达快速定位查询点所在道路，进而计算出道路最近邻点，并且结合文献[1]的算法计算其最近邻点。

1 研究方法

本文定义全部道路构成无向边的集合E{ei|i∈I}，I为道路编号的集合；道路端点构成顶点集合V{vi|i∈I}，I为顶点编号的集合；道路内的数据点P{pi|i∈I}，I为数据点编号的集合。

1.1 道路分割

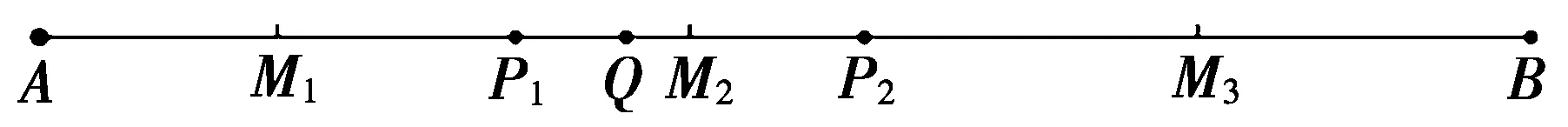
图1 道路分割图

当查询点Q落在某一子线段上，可以证明，若该子线段包含数据点，该数据点即所查找的最近邻点；若该子线段不包含数据点，则必是道路端点，以该端点为起点通过INE算法[1]查找相邻道路最近邻点。具体证明如下：

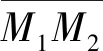
显然，除数据点P1、P2外，其他数据点距离查询点Q更远，因此，只需证明P1和P2中哪个数据点距离查询点Q更近。

1.2 格网划分

i=k×n+l，k∈0,…,m；l∈0,…,n。

(1)

受Bresenham算法的启发，本文计算每条道路经过的单元格，并且记录每个单元格所包含的子道路。道路经过的单元格如图3所示。

图2 查询区域格网划分

图3 道路经过的单元格

根据笛卡尔二维坐标系，以道路一个端点为坐标原点，按照道路所在象限可分为4个方向，不考虑道路方向，即无向图情况下，可将道路分为2个方向，道路边的斜率k≥0或k<0。因此，可将4个方向的道路简化为2个方向，计算道路经过的单元格，并记录每个单元格包含的子道路。

1.3 矩形划分

作为对比，还设计了单向格网划分，或者称之为矩形划分，利用分治法的思想，将查询区域进行格网划分，只在水平或者垂直方向进行等比例划分。这里以垂直方向划分为例进行分析，水平方向与之类似。

图4 查询区域矩形划分

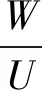
1.4 获取查询点最近邻点

根据式(1)，由查询点坐标(x0,y0)获取查询点所在单元格，这里假设查询点总是在某条道路上，从而，在查询点所在单元格包含的子道路集合中必有一条子道路包含该查询点，所以，由点到直线的距离为：

(2)

计算查询点到所在单元格内所有子道路的距离Di，使得Di=0的子道路sei即为查询点所在子道路。根据图1，由上文可知：当该子道路包含数据点时，例如M1M2、M2M3，该数据点即查询点最近邻点；当该子道路不包含数据点时，例如AM1、M3B，该子道路必包含所属道路端点，以此端点为起点，通过INE算法[1]计算查询点最近邻点。

2 实验数据

本文的原始数据来自美国5个城市的地图数据[17]，分别是加利福尼亚(CA)、旧金山(SF)、北美(NA)、圣华金县(TG)和奥尔登堡(OL)。

原始数据由顶点和道路构成，其中，顶点V(ID,X,Y)由顶点编号和坐标构成；道路R(ID,start_ID,end_ID)由道路编号、起点编号和终点编号构成。

根据原始数据的顶点和道路,手动设置边上是否有数据点以及数据点的数量。本文按照比率P0随机获取N×P0条边的索引，其中，N为边的总数，对于这些边的每条边，按照边上包含的数据点不超过M个,以比率P1随机获取M×P1个百分比P{pi|i≤M×P1}，pi表示第i个数据点到所在边起始点距离与边长的百分比，由此计算第i个数据点到所在边起始点距离，生成道路数据点，其中，数据点DP(ID,X,Y,R_ID)由道路数据点编号、坐标和所在道路编号构成。按照以上方法，可生成查询点QP(ID,X,Y)，

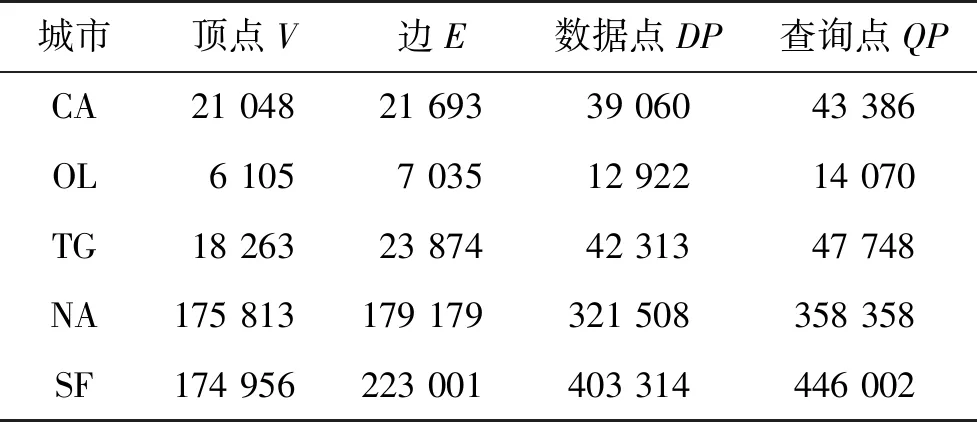
表1 美国5个城市的顶点、边、数据点和查询点

由查询点编号和坐标构成。美国5个城市的顶点、边、数据点和查询点如表1所示。

3 实验结果与分析

本文按照划分查询区域设置不同比率p，包含数据点边的顶点数与总顶点数比率p0=0.005，数据点的边数与总边数的不同比率p1，边上包含数据点的最大数量p2=5，边上包含查询点的最大数量p3=2，对不同城市进行实验分析，具体设置如表2所示。

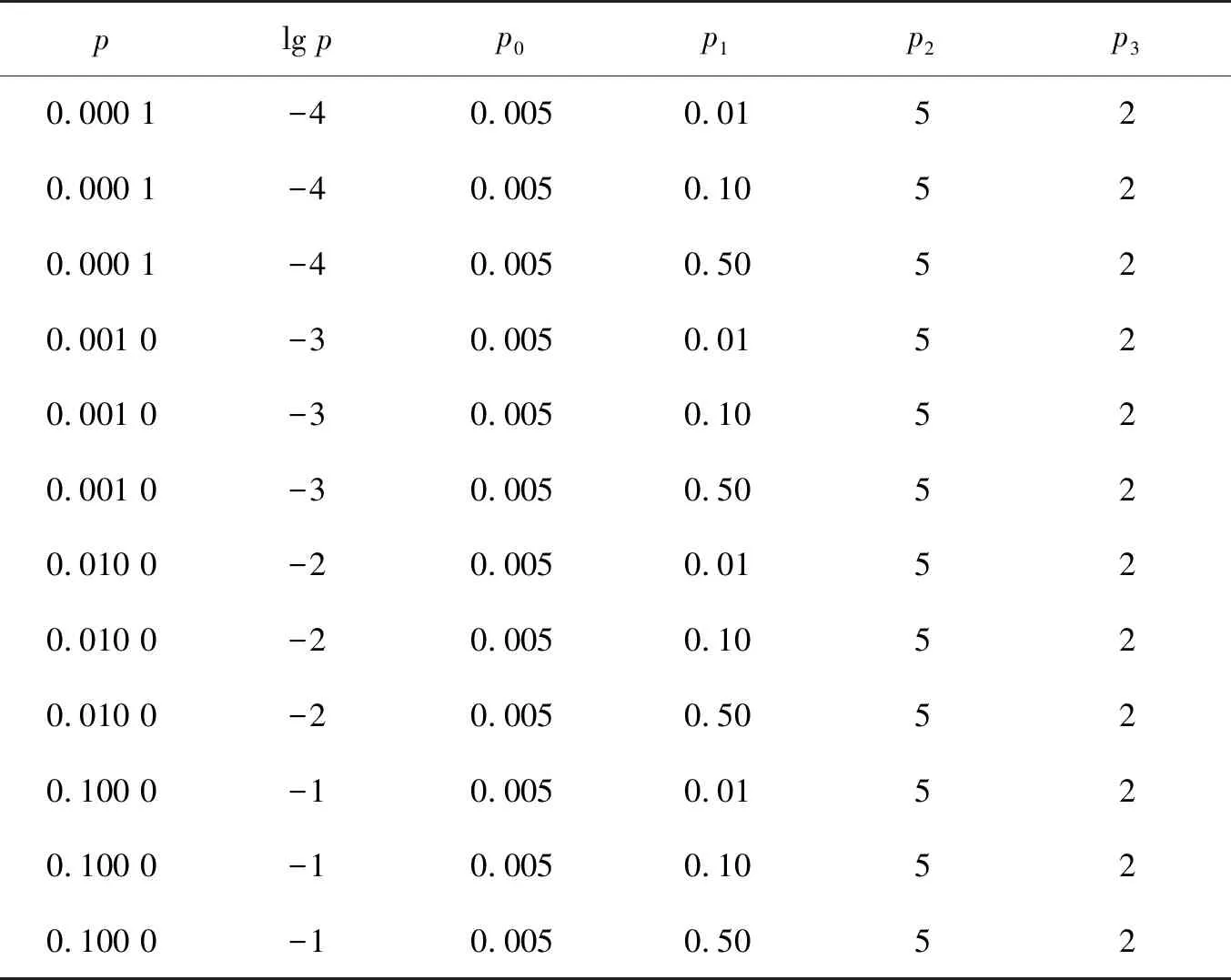
表2 查询区域划分设置

根据表1的设置，分别对美国5个城市进行实验，按包含数据点的边数与总边数比率p1=0.5的情况，对查询区域划分比率lgp分别为-4，-3，-2，-1的格网划分、矩形划分、INE算法查询效率进行实验分析，美国5个城市平均查询时间如图5所示。

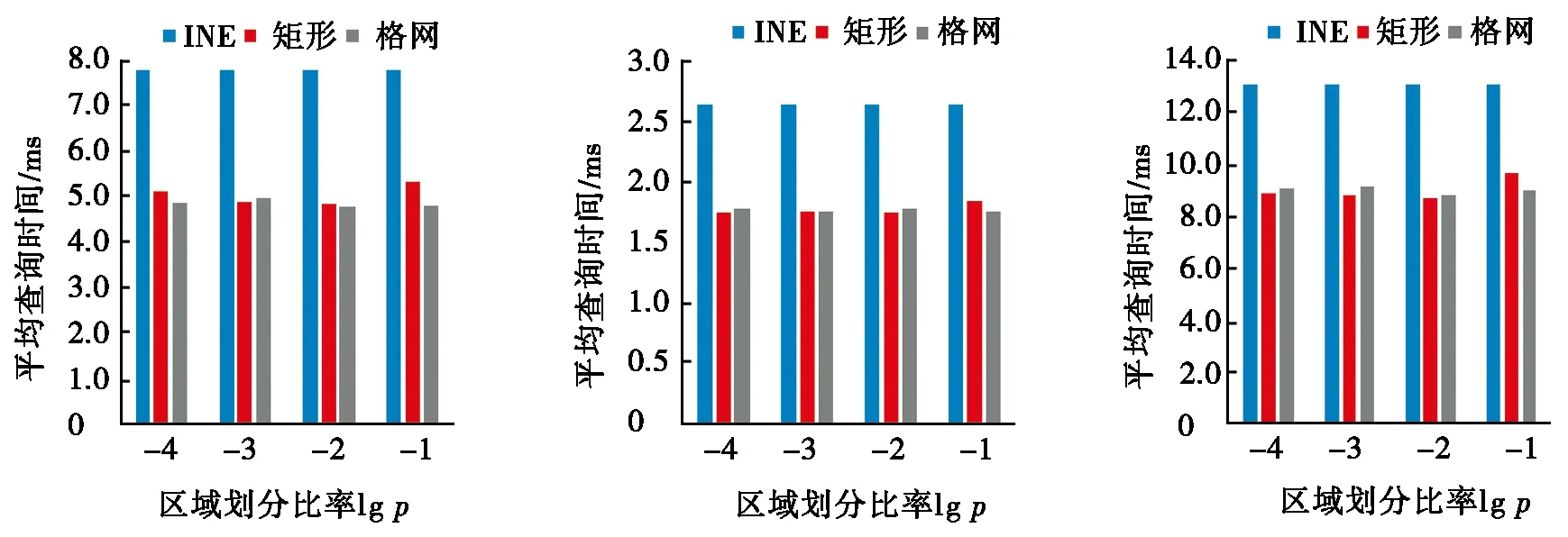
(a) CA (b) OL (c) TG

(d) NA (e) SF

图5 美国5个城市平均查询时间

由图5可知：随着格网划分比率的增大，格网划分算法的平均查询时间明显低于现有INE算法。由图5a可知：在查询区域数据点较少的情况下，矩形划分与格网划分查询时间差别较小，这主要是由于数据点较少时，矩形包含的数据点数量与格网包含的数据点数量差别较小所致，甚至可能是矩形划分查询时间比格网划分查询时间更小，如图5b和图5c所示。这说明当数据点比较少时，矩形划分与格网划分效果差别不大，从资源占用角度分析，当数据点数量不大时，使用矩形划分更为合理。由图5d和图5e可知：当数据点数量极大时，格网划分查询时间明显优于矩形划分查询时间，这也说明了当数据量极大时，矩形包含的数据点数量远大于格网包含的数据点数量，使得定位查询点时间较长，以上分析更加说明了格网划分算法在大数据量下查询效率提升显著。

图6为SF不同数据点平均查询时间。由图6可知：当同一地区包含数据点数量不同时，基于格网划分的查询时间与INE算法的查询时间有明显不同。由图6a可以看出：当数据点较少时，格网划分查询时间与INE算法的查询时间相近，这是由于数据点较少时，数据点出现在边的端点的概率较大，而INE算法是基于顶点查询的，因此当数据点较少时格网划分将退化为INE算法。由图6b和图6c可以看出：随着数据点数量的增加，格网划分的查询时间明显优于INE算法的查询时间。

(a)p1=0.01(b)p1=0.10(c)p1=0.50

图6 SF不同数据点平均查询时间

对比分析图5和图6可知：随着格网划分比率的增大，格网划分算法的平均查询时间明显低于现有INE算法，同时矩形划分介于格网划分与INE算法之间，这说明对查询区域进行划分有效地降低了查询时间；另一方面，说明划分区域过大对提升查询效率是有限的。其次，通过图6a可以看出：当包含数据点的边数与总边数比率p1为0.01时，即在边上的数据点不多的情况下，3种算法的平均查询时间基本一致，这也表明本文的格网划分算法对数据点大量在边上的查询效率明显，当边上数据点不多的情况下，退化为INE算法。由图6可以看出：对于不同比率p1，随着格网划分比率的增大，格网划分算法的平均查询时间都远小于INE算法的查询时间，表明本文的算法对于超大数据量的执行效率更高。

4 结束语

大数据量的道路最近邻查询效率问题的解决一直存在困难，尤其是数据点在边上而不只是作为边的顶点出现，本文提出的算法通过将大图划分为小图的分治思想，有效地解决了这个问题，并且提高了查询效率。根据实验结果分析，计算查询点所在最近邻，若查询点所在子道路包含数据点则时间复杂度为O(1)，反之，则和INE算法复杂度相同。

本文算法不仅可以在道路最近邻查询中有很好的应用，也可应用在其他最近邻相关算法，采用格网划分可以避免全局搜索带来的效率低下问题。同时，可以应用到地理信息系统及全球定位系统定位服务当中，下一步将对格网划分查询算法内存占用进行优化，以进一步提升效率。