滑模控制的多混沌系统组合函数投影同步

方 洁,娄新杰,许丹莹，邓 玮

(郑州轻工业大学 电气信息工程学院,河南 郑州 450002)

0 引言

混沌同步是混沌研究的一个重要方向，随着混沌理论的发展，混沌同步在电子电路、生物工程、保密通信等领域的应用越来越广泛，混沌同步控制已成为非线性科学的一个重要研究热点[1-3]。到目前为止，各类同步现象及特性已经被相继提出，如完全同步[4]、反同步、相同步、投影同步[5]、延迟同步、广义同步[6]、组合同步[7]和函数投影同步[8]等。

组合同步是指多个主从系统之间按照某种关系实现同步,选择不同的组合参数和组合形式，组合同步涵盖了大多数其他同步类型，是一种更广义的同步方法。近年来，组合同步作为一种较为新颖的同步类型引起了科研人员的兴趣。文献[9]利用李雅普诺夫稳定性理论，得到了对偶组合多开关的充分条件，实现了4个驱动系统与4个响应系统之间的组合同步。文献[10]采用多开关同步的方法，将2种混沌驱动系统与1种混沌响应系统进行同步，得出了3种混沌系统实现理想同步的充分条件。文献[11]基于李雅普诺夫稳定性理论设计相应的控制器，实现了3个同构超混沌复系统之间以及混沌复系统和实系统之间的组合复同步。

函数投影同步通过引入函数比例因子,实现系统状态按照函数比例关系同步,将其应用于保密通信中，可增强信息的安全性。近年来，已有多位学者对函数投影同步进行了研究。文献[12]在参数未知的情况下，通过设计非线性控制器和参数自适应律，实现了两个不同的复混沌系统的修正函数投影同步。文献[13]基于分数阶系统的稳定性理论和跟踪控制方法，设计了一种分数阶混沌系统控制器，实现了不同阶数的分数阶混沌系统之间的函数投影同步。文献[14]针对已知和未知混沌系统参数，分别提出了两种自适应控制方案，使一类整数阶混沌系统与分数阶混沌系统之间进行自适应修正广义函数投影同步。文献[15]基于李雅普诺夫稳定性理论，设计了一种鲁棒自适应控制器，实现了具有不确定参数和扰动的5项混沌系统的完全切换修正函数投影同步。文献[16]采用自适应控制技术，得出一组能够实现复修正函数投影同步的充分条件，实现了具有任意复参数的复变量混沌系统之间的复修正函数投影同步。现有的函数投影同步研究主要集中在单驱动系统和单响应系统的同步方案上，对多驱动系统和多响应系统之间的组合同步研究相对较少。如何将组合同步和函数投影同步相结合，研究多个混沌系统之间的组合函数投影同步问题是一个新的课题。

滑模控制是一种特殊的非线性控制方法，其通过开关函数对系统状态进行不连续的切换控制，能消除系统对外部扰动和系统内部参数变化的敏感性，具有很强的鲁棒性。本文利用滑模控制的抗干扰性，结合主动控制方法，设计相应的滑模面和控制器，实现了2个混沌驱动系统和多个混沌响应系统的组合函数投影同步。利用连续函数替代控制律中的非连续符号函数，消除了滑模控制器的抖振问题。该组合同步方式中，混沌驱动系统和混沌响应系统可以扩展为3个或者多个混沌系统进行同步，具有一定的通用性。基于李雅普诺夫稳定性理论的理论分析和数值仿真，证明了所设计控制器的有效性。

1 问题描述

本文设计的基于滑模控制的多混沌系统组合函数投影同步，由2个混沌驱动系统和多个混沌响应系统组成。第1个混沌驱动系统定义为：

(1)

其中：x1(t)=[x11(t),x12(t),…,x1n(t)]T为混沌驱动系统(1)的状态变量；f1(x1(t))为非线性连续函数，f1(x1(t))=[f11(x1(t)),f12(x1(t)),…,f1n(x1(t))]T。混沌驱动系统(1)的扰动项为A1(t)=[a11(t),a12(t),…,a1n(t)]T。

混沌驱动系统(1)的响应系统可写为：

(2)

其中：xj(t)=[xj1(t),xj2(t),…,xjn(t)]T是响应系统(2)的状态变量;fj(xj(t))=[fj1(xj(t)),fj2(xj(t)),…,fjn(xj(t))]T，fj1(xj(t))，fj2(xj(t))，…，fjn(xj(t))是非线性连续函数;Aj(t)=[aj1(t),aj2(t),…,ajn(t)]T为响应系统(2)的扰动项。控制器为uj-1(t)=[uj-1,1(t),uj-1,2(t),…,uj-1,n(t)]T,j=2,3,4,…,N。

第2个混沌驱动系统定义为：

(3)

其中：y1(t)=[y11(t),y12(t),…,y1n(t)]T为混沌驱动系统(3)的状态变量;g1(y1(t))是非线性连续函数，g1(y1(t))=[g11(y1(t)),g12(y1(t)),…,g1n(y1(t))]T。混沌驱动系统(3)的扰动项为B1(t)=[b11(t),b12(t),…,b1n(t)]T。

混沌驱动系统(3)的响应系统为：

(4)

其中：yj(t)=[yj1(t),yj2(t),…,yjn(t)]T为响应系统(4)的状态变量;gj(yj(t))=[gj1(yj(t)),gj2(yj(t)),…,gjn(yj(t))]T；gj1(yj(t))，gj2(yj(t))，…，gjn(yj(t))为非线性连续函数；Bj(t)=[bj1(t),bj2(t),…,bjn(t)]T为响应系统(4)的扰动项；控制器为vj-1(t)=[vj-1,1(t),vj-1,2(t),…,vj-1,n(t)]T,j=2,3,4,…,N。

定义1分别将驱动系统x1(t)和驱动系统y1(t)、响应系统x2(t)和响应系统y2(t)、响应系统x3(t)和响应系统y3(t)、…、响应系统xj(t)和响应系统yj(t)进行组合,定义ej-1(t)=x1(t)+y1(t)-Mj(t)[xj(t)+yj(t)],如果时间t达到无穷大时，满足

(5)

则称驱动-响应系统实现了组合函数投影同步。其中：ej-1(t)=[ej-1,1(t),ej-1,2(t),…,ej-1,n(t)]T；Mj(t)(j=2,3,…,N)为一个函数比例因子矩阵；mj1,mj2,…,mjn为非零的函数比例因子。

如果函数比例因子矩阵M是常数矩阵，那么组合函数投影同步问题将转化为组合投影同步问题。如果函数比例因子矩阵M=I或M=-I，那么组合函数投影同步问题将转为组合完全同步问题或组合反同步问题，其中I是一个n×n的单位矩阵。

由式(5)可得同步系统的动态误差为：

f1(x1(t))+A1(t)+g1(y1(t))+B1(t)-Mj(t)[fj(xj(t))+Aj(t)+uj-1(t)+

f1(x1(t))+g1(y1(t))+A1(t)+B1(t)-Mj(t)[Aj(t)+Bj(t)]-

f1(x1(t))+g1(y1(t))+A1(t)+B1(t)-Mj(t)[Aj(t)+Bj(t)]-

(6)

其中：wj-1(t)=Mj(t)[uj-1(t)+vj-1(t)](j=2,3,4,…,N)为总控制器。

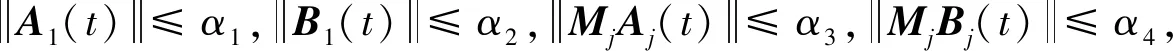
2 无抖振滑模控制器设计

2.1 滑模面设计

首先，定义一个非奇异端面sj-1(t)；其次，确定控制律来保证混沌系统的运动轨迹沿设计好的滑模面滑动。滑模面的定义为：

sj-1(t)=λj-1ej-1(t)，

(7)

其中：sj-1(t)=[sj-1,1(t),sj-1,2(t),…,sj-1,n(t)]T(j=2,3,4,…,N)是一组函数变量；λj-1(t)=[λj-1,1(t),λj-1,2(t),…,λj-1,n(t)]T(j=2,3,4,…,N)是一组常数向量。

设计如下的滑模到达律：

(8)

当系统处于滑模面上，被控系统须满足如下条件：

(9)

因此，设计的组合控制器为wj-1(t)=Mj(t)[uj-1(t)+vj-1(t)]，保证动态系统的运动轨迹在滑模面上滑动。

2.2 无抖振滑模控制器设计

为了确保误差系统轨迹到达并保持在已设定的滑模面上，可设计如下滑模控制器：

wj-1(t)=Mj(t)[uj-1(t)+vj-1(t)]=

f1(x1(t))+g1(y1(t))-Mj(t)[fj(xj(t))+gj(yj(t))]-

(10)

其中：ρj-1=[ρj-1,1,ρj-1,2,…,ρj-1,n]T;j=2,3,4,…,N。

将控制器(10)代入式(6)，可以进一步求得同步动态误差：

A1(t)+B1(t)-Mj(t)[Aj(t)+Bj(t)]+ρj-1θj-1(t)。

(11)

相应的参数自适应律为：

(12)

其中：qj-1>α;j=2,3,4,…,N。

根据式(6)、滑模到达律(8)和自适应律(12)可以得出：

(13)

定理1对于定义1中的具有外界干扰的混沌组合同步误差系统ej-1(t)=x1(t)+y1(t)-Mj(t)×[xj(t)+yj(t)]，在控制器(10) 和自适应律(12)的作用下，误差系统(5)将渐近收敛到零。

证明选择正定的李雅普诺夫泛函为：

(14)

对其求导可得：

(15)

根据式(6)和式(7)可以得出：

λj-1sj-1(t){f1(x1(t))+g1(y1(t))+A1(t)+B1(t)}-

λj-1sj-1(t){Mj(t)[fj(xj(t))+gj(yj(t))]+Mj(t)[Aj(t)+Bj(t)]}-

(16)

(17)

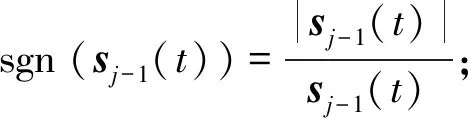
(18)

λj-1sj-1(t){A1(t)+B1(t)-Mj(t)[Aj(t)+Bj(t)]}-|sj-1(t)|qj-1≤

(19)

即

(20)

因为控制器(10)中有不连续的符号函数sgn(sj-1(t))，会产生不期望的抖振，为避免抖振现象，在实际中可用双曲正切函数tanh (sj-1(t)/ϑ)(ϑ>0)代替符号函数，其中，ϑ是适当大的正常数。最后的控制器为：

wj-1(t)=Mj(t)[uj-1(t)+vj-1(t)]=

f1(x1(t))+g1(y1(t))-Mj(t)[fj(xj(t))+gj(yj(t))]-

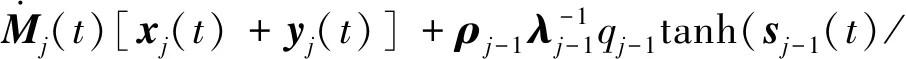
(21)

其中：ρj-1=[ρj-1,1,ρj-1,2,…,ρj-1,n]T;j=2,3,4,…,N。

3 数值仿真

为了验证上述方案的正确性，分别以Lorenz混沌系统和Chen混沌系统作为第1个驱动系统和第2个驱动系统[17]，分别以Genesio-Tesi混沌系统[18]和Liu混沌系统[19]作为第1个响应系统和第2个响应系统进行仿真实验。

Lorenz混沌系统的微分方程[17]中x11、x12、x13为状态变量，当参数β1=10、β2=28、β3=8/3时，系统处于混沌状态；a11、a12、a13为驱动系统的外界扰动。Chen混沌系统的微分方程[17]中x21、x22、x23为状态变量，当参数ω1=35,ω2=3,ω3=28时，系统处于混沌状态；a21、a22、a23为响应系统的外界干扰；u11、u12、u13为响应系统的控制器。Genesio-Tesi混沌系统的微分方程[18]中y11、y12、y13为状态变量，当参数ε1=-6.00、ε2=-2.92、ε3=-1.20时，系统处于混沌状态;b11、b12、b13为驱动系统的外界干扰。Liu混沌系统的微分方程[19]中y21、y22、y23为状态变量，当参数φ1=10.0、φ2=40.0、φ3=1.0、φ4=2.5、φ5=4.0时，系统处于混沌状态;b21、b22、b23为响应系统的外界干扰;v11、v12、v13为响应系统的控制器。

假设干扰项为：A1=[0.2cos (2t),0.2cos (2t),0.2cos (2t)]T;A2=[0.2cos (2t),0.2cos (2t),0.2cos (2t)]T;B1=[0.2cos (2t),0.2cos (2t),0.2cos (2t)]T;B2=[0.2cos (2t),0.2cos (2t),0.2cos (2t)]T;函数比例因子矩阵为M(t)，M(t)=[2+sint,3+sint,4+sint]T。

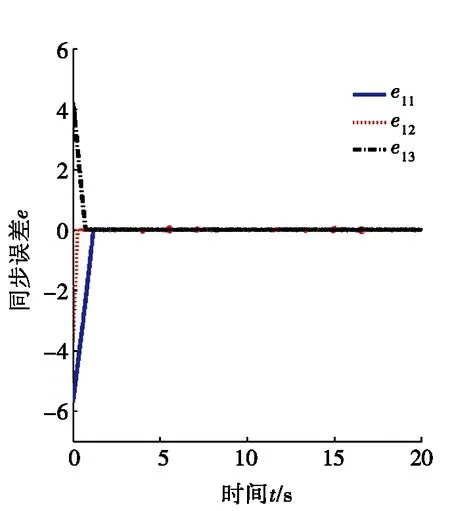
图1 同步误差e11，e12，e13随时间t的变化曲线

运用MATLAB软件进行仿真，取驱动系统的初始值分别为(x11(0),x12(0),x13(0))=(1.0,0.5,3.0)，(x21(0),x22(0),x23(0))=(1,0,5)，取响应系统的初始值分别为(y11(0),y12(0),y13(0))=(0.6,1.0,6.0)，(y21(0),y22(0),y23(0))=(0,1,0)；取λ1=[1 1 1]T、ρ1=[1 1 1]T，q1=5，q2=15，q3=5，可以得出仿真图，如图1～图3所示。

图1中同步误差e渐近收敛于零，说明驱动系统与响应系统通过滑模控制实现了组合函数投影同步。图2为驱动系统和响应系统相应的函数比例因子m3(t)随时间的变化曲线。由图2可知：函数比例因子m3(t)与4+sint图形基本保持一致。图3为驱动系统和响应系统状态变量的演化曲线，即x13+y13和x23+y23随时间t的变化曲线。由图3可知：经过短暂的振荡后，驱动系统和响应系统可以按照相应的函数比例因子实现同步，即(x23+y23)=(4+sint)(x13+y13)。综合图1～图3可知：在存在外部扰动和抖振的情况下，驱动-响应系统按照相应的函数比例因子实现了同步，说明该混沌组合函数投影同步方法具有一定的鲁棒性。

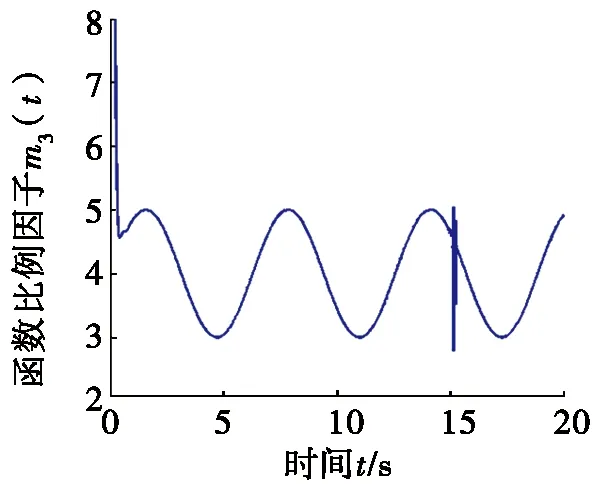
图2 函数比例因子m3(t)随时间t的变化曲线

图3x13+y13和x23+y23随时间t的变化曲线

4 结束语

本文研究了基于滑模控制的多混沌系统组合函数投影同步，理论分析和数值仿真结果表明，驱动-响应系统能够在干扰和抖振的影响下实现同步。该组合同步方案中混沌驱动系统和混沌响应系统可以扩展为3个或者多个混沌系统，一方面，组合同步的复杂性和函数比例因子的多样性能有效增强保密通信的安全性;另一方面,滑模控制的快速响应特性可以减少加密解密时间，从而降低破译风险。本文研究结果拓展了多混沌系统的同步控制方案，为混沌同步应用于保密通信和信息传输等领域提供了新思路。