人工势场法局部极小值的研究

郜 辉，吕志刚，王 宾，夏开成，毛 琳，王 辛，李 彬

(西安工业大学电子信息工程学院，陕西 西安 710021)

0 引言

人工势场法是Khatib首次提出的理论，它的基本思想是将整个环境转化为一个巨大的人工势场模型[1]，将移动机器人看做为一个运动的质点，该质点位于整个势场内，同时移动机器人运动的目标点自身产生吸引力势场[2]，环境中的所有障碍物会产生排斥力势场，移动机器人在环境中运动时会受到2种类型力的作用[3]，第1种是最终目标点的引力势场对移动机器人产生的吸引力，第2种是移动机器人运行过程中所有障碍物的排斥势场对移动机器人产生的排斥力[4]。移动机器人在整个运动过程中所受的合力由目标点对移动机器人的引力和所有障碍物对移动机器人的斥力组成，移动机器人在引力与斥力的合力牵引下从起点移动到目标点，完成局部路径规划[5]。

人工势场法从产生之初一直是移动机器人避障算法中的重要算法[6]。因为人工势场法原理简单，生成的路径光滑，而且实时性好，也可以保证移动机器人的安全，避免和障碍物接触，所以人工势场法适合用在环境相对简单、障碍物少的场景中，不适合在复杂的障碍物场景中[7]。人工势场法的弊端有：当目标点距离障碍物太近，导致移动机器人所受障碍物斥力大于目标点吸引力，移动机器人出现目标不可达现象；当移动机器人运动环境复杂时容易产生引力和斥力的平衡状态，从而陷入局部极小点，导致移动机器人停止不前；另外移动机器人如果利用人工势场法在障碍物前或在狭窄通道中运行时，极易产生振荡现象[8]。

对于人工势场法的研究由来已久，已经有很多学者对人工势场法的缺陷进行了改进[9]。文献[10]引入了预测距离，并设置了虚拟目标点，在机器人还未陷入局部极小点之前使用虚拟目标点牵引移动机器人走出局部极小点；文献[11]对引力场函数进行了改进，并在无人机陷入局部极小点后，以障碍物边界为子目标点，使无人机可以飞出局部极小点，但是由于是以障碍物边界为子目标点，有可能导致无人机碰撞障碍物。

在此，针对局部极小值问题，对4种局部极小值解决办法进行讨论分析。其中，增加子目标点的方式与绕障碍物走的方式成功解决了局部极小点问题，成功抵达了目标点，并通过仿真实验验证了增加障碍物排斥力方法解决局部极小点问题的局限性。

1 传统人工势场法

人工势场法的基本原理就是将移动机器人假设成1个质点，将移动机器人所在的环境假想成1个虚拟力场[12]，移动机器人在虚拟力场中运动，虚拟力场是由目标点对移动机器人的引力场和障碍物对移动机器人的斥力场组成。所有的障碍物对移动机器人均有斥力作用[13]，根据障碍物距离的远近确定斥力场的大小，引力场由目标点产生。因此，人工势场法的势场函数就是引力场与斥力场的和，如式(1)所示。移动机器人的移动方向为势场函数下降的方向，即势场下移动机器人的合力受力方向。

U(q)=Uatt(q)+Urep(q)

(1)

q为移动机器人当前的坐标点；Uatt(q)为移动机器人的引力势场[14]；Urep(q)为移动机器人的斥力势场；U(q)为移动机器人在势场中所受的总势场和。

在虚拟力场中移动机器人受到的总牵引力为当前位置总势场的负梯度，移动机器人的牵引力由引力和斥力组成，在虚拟力场中引力是引力场的负梯度，斥力是斥力场的负梯度[15]。因此，移动机器人在势场中所受力为

F(q)=Fatt(q)+Frep(q)-

Uatt(q)-Urep(q)

(2)

F(q)为移动机器人在虚拟力场中受到的总的合力；Fatt(q)为移动机器人受目标点的引力，引导移动机器人走向目标点；Frep(q)为移动机器人所受的总斥力，使移动机器人远离障碍物[16]。

由于在移动机器人避障过程中，只受1个目标点牵引，但是会有多个障碍物同时对移动机器人进行作用，所以移动机器人在虚拟力场中斥力场与斥力不能单一的进行计算，需要计算多个障碍物对移动机器人的斥力总和[17]，移动机器人在虚拟力场中斥力为

Frep(q)=∑nFrep(q)-∑nUrep(q)

(3)

n为整个环境中的障碍物个数。移动机器人在环境中受力分析如图1所示，其中F为移动机器人所受合力。

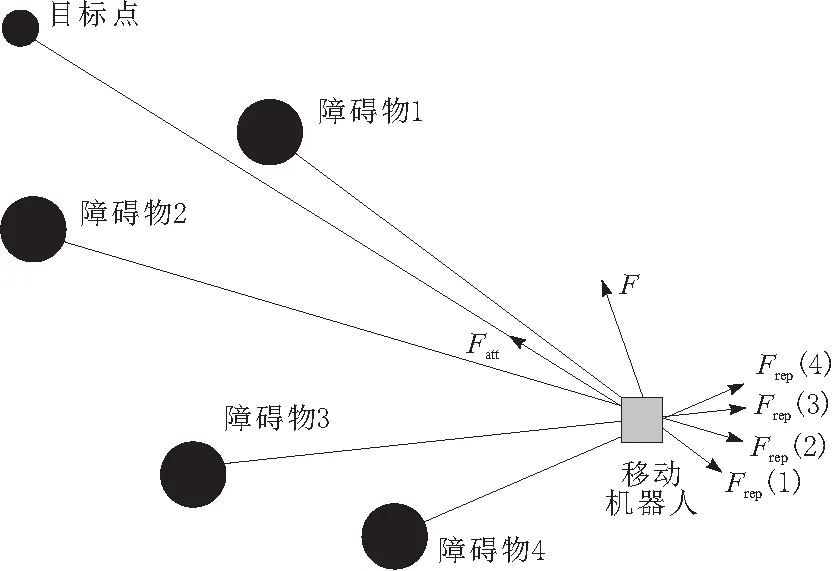
图1 移动机器人受力分析

如图1所示，在移动机器人所处的环境中，共有4个障碍物和1个目标点。移动机器人受到目标点产生的吸引力Fatt，受到障碍物1产生的排斥力Frep(1)，受到障碍物2产生的排斥力Frep(2)，受到障碍物3产生的排斥力Frep(3)，受到障碍物4产生的排斥力Frep(4)，故移动机器人在当前位置共受到5个力的作用，5个力的合力为F。此外，移动机器人在当前位置的受力方向和运动方向也与F一致，在合力F的牵引下，移动机器人逐步抵达目标点。

2 人工势场法的缺陷

传统的人工势场法在进行路径规划时，由于算法的特性原因，导致了传统的人工势场法有3个缺陷，如下所述。

a.缺陷一：局部极小值问题。当移动机器人在虚拟力场中所受引力与斥力大小相等、方向相反时，移动机器人处于受力平衡状态，当前位置所受合力为0，此时移动机器人陷入了局部极小值点[18]。移动机器人在局部极小值点附近的所有点位的合力都指向局部极小值，使得移动机器人无法走出该区域，或者在该区域产生振荡[19]。

b.缺陷二：受力不平衡问题。传统人工势场法引力场函数与移动机器人和目标点距离成正比，当移动机器人距离目标点较远时，引力场函数产生的引力过大，可能导致移动机器人与障碍物相撞[20]。

c.缺陷三：目标不可达问题。当此次路径规划中将目标点设置的位置距离障碍物很近时，障碍物会影响移动机器人的运动，障碍物产生的斥力会大于目标点产生的引力，导致移动机器人无法到达目标点，造成移动机器人的目标不可达问题[21]。

3 局部极小值问题的改进

人工势场法的局部极小值问题必须进行改进，改进算法有很多种，本文选用了4种解决局部极小值问题的办法，进行了算法仿真验证，并对比分析了4种解决办法的优缺点。4种解决办法如下所述。

a.当移动机器人进入局部极小值之后，增加障碍物斥力，打破原有的平衡状态，迫使移动机器人走出局部极小值位置。

b.当移动机器人进入局部极小值之后，采用“绕墙走”的方式，围绕障碍物的边缘进行运动，使移动机器人走出局部极小值位置。

c.当移动机器人进入局部极小值之后，采用自动添加子目标点的方式，利用子目标点的牵引力引导移动机器人走出局部极小值位置，然后再从子目标点运动到最终的目标点。

d.当移动机器人进入局部极小值之后，采用人为添加子目标点的方式，利用子目标点的牵引力引导移动机器人走出局部极小值位置，然后再从子目标点运动到最终的目标点。

仿真实验场景选用的是648×1 152的位图地图，地图障碍物分布情况如图2所示(图中坐标数值进行了无量纲化处理，只表示场景大小，没有具体单位，图3～图8类似)。

图2 648×1 152地图障碍物分布情况

本次路径规划中相关参数设置为：起点位置为(50,500)；目标点位置为(1 100,50)；移动机器人单步最大移动距离为2；移动机器人大小为10×10,长为10，高为10；吸引势因子参数为300 000 000；排斥势因子参数为300 000。

在当前参数的设置下，移动机器人在传统人工势场算法下的路径规划如图3所示。

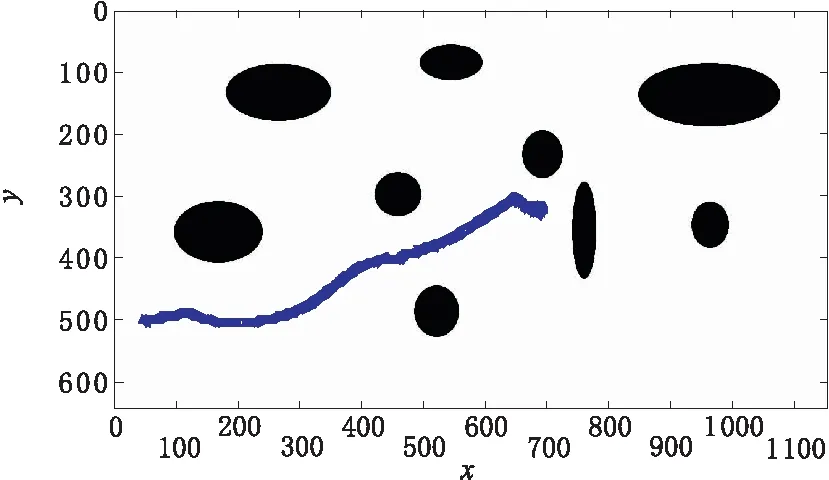
图3 传统人工势场算法下的路径规划

图3中，粗线条为人工势场法的路径，显而易见，此方法陷入了局部极小值。因此，下面将分别使用4种方法解决传统人工势场法的局部极小值问题。

3.1 增加障碍物斥力解决局部极小值问题

当移动机器人进入局部极小值之后，增加障碍物斥力，打破原有的平衡状态，迫使移动机器人走出局部极小值位置。

系统初始运行参数为：起点位置为(50,500)；目标点位置为(1 100,50)；移动机器人单步最大移动距离为2；移动机器人大小为10×10,长为10，高为10；吸引势因子参数为300 000 000；排斥势因子参数为300 000。

当移动机器人进入局部极小值位置后，增加障碍物排斥式因子参数，增大障碍物排斥力，使移动机器人摆脱当前的局部极小值位置，当障碍物排斥势因子参数由300 000增加到300 000 000时，仿真结果如图4所示。

由图4可知，增大障碍物排斥因子参数后，障碍

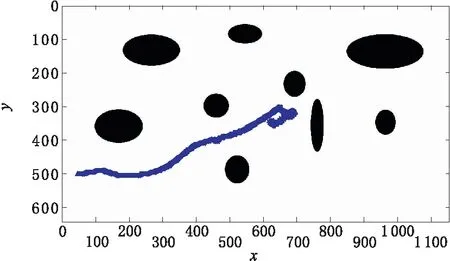
图4 增加障碍物排斥因子的仿真结果

物排斥力增大，移动机器人从原来的局部极小值位置走出，但是随后进入了新的局部极小值位置。由此可知，采用增加障碍物排斥力的方式可以使移动机器人走出局部极小值，但是并不能确保移动机器人成功抵达目标点，适用场景比较少。

3.2 “绕墙走”方式解决局部极小值问题

当移动机器人进入局部极小值之后，采用“绕墙走”的方式，围绕障碍物的边缘进行运动，使移动机器人走出局部极小值位置。

系统初始运行参数如下：起点位置为(50，500)；目标点位置为(1 100，50)；移动机器人单步最大移动距离为2；移动机器人大小为10×10,长为10，高为10；吸引势因子参数为300 000 000；排斥势因子参数为300 000。

采取“绕墙走”方式仿真结果如图5所示。

图5 “绕墙走”方式解决局部极小值的仿真结果

由图5可知，当移动机器人陷入局部极小值后，移动机器人绕着局部极小值位置上方的障碍物采取了“绕墙走”方式进行运动，当绕行过障碍物之后继续执行原来的算法，移动机器人成功抵达了目标点。由此可知，采用“绕墙走”方式可以成功地解决局部极小值问题，使移动机器人抵达目标点。

3.3 自动添加子目标点解决局部极小值问题

当移动机器人进入局部极小值之后，采用自动添加子目标点的方式，利用子目标点的牵引力引导移动机器人走出局部极小值位置，然后再从子目标点运动到最终的目标点。

系统初始运行参数为：起点位置为(50，500)；目标点位置为(1 100，50)；移动机器人单步最大移动距离为2；移动机器人大小为10×10,长为10，高为10；吸引势因子参数为300 000 000；排斥势因子参数为300 000。

当移动机器人陷入局部极小值后，算法自动生成子目标点(1 000，600)，仿真结果如图6所示。

图6 自动生成子目标点(1 000，600)的仿真结果

当移动机器人陷入局部极小值后，算法自动生成子目标点(764，500)，仿真结果如图7所示。

图7 自动生成子目标点(764，500)的仿真结果

由图6和图7可知，利用自动生成子目标点这种方式可以使移动机器人成功地走出局部极小位置，抵达目标点，但是由于子目标点位置是随机生成的，路径的长度不是最优的，并且路径的随机性比较大，只有通过多次实验才能选出最优的路径。

3.4 手动添加子目标点解决局部极小值问题

当移动机器人进入局部极小值之后，采用人为添加子目标点的方式，利用子目标点的牵引力引导移动机器人走出局部极小值位置，然后再从子目标点运动到最终的目标点。

系统初始运行参数为：起点位置为(50，500)；目标点位置为(1 100，50)；移动机器人单步最大移动距离为2；移动机器人大小为10×10,长为10，高为10；吸引势因子参数为300 000 000；排斥势因子参数为300 000。

当移动机器人陷入局部极小值后，人为的手动添加子目标点(760，200)，仿真结果如图8所示。

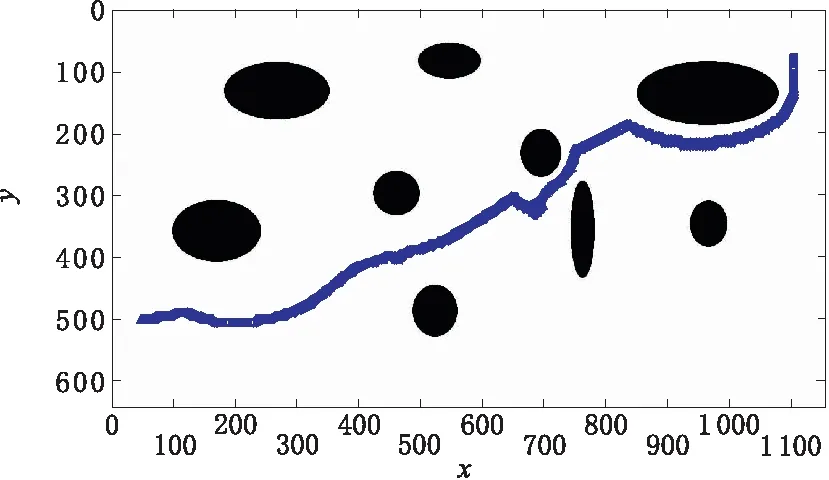
图8 手动添加子目标点(760，200)的仿真结果

由图8可知，采用手动添加子目标点的方式可以使移动机器人成功的走出局部极小位置，抵达目标点，而且路径距离最短，是所有解决局部极小值问题方法中最好的方法。

4 算法仿真结果分析

解决局部极小值问题的4种方法仿真验证结果如表1所示。

表1 解决局部极小值仿真结果

由表1可知，采用增加障碍物斥力的方式不一定能使移动机器人抵达目标点，不是一种优良的算法改进方式；采用“绕墙走”方式可以使移动机器人摆脱局部极小值抵达目标点，但是路径上距离障碍物较近，容易产生碰撞，对于一些要求不太高的场景可以采用此种方式进行路径规划；采用自动生成子目标点的方式可以使移动机器人摆脱局部极小值抵达目标点，但是通过仿真发现，每次的子目标点位置都不一致，导致路径长度不确定，缺乏稳定性；采用人为添加子目标点的方式可以使移动机器人摆脱局部极小值并抵达目标点，并且路径长度短、路径安全性高，是4种方法中最有效的方法。

5 结束语

通过4种不同的方法对人工势场法的局部极小值问题进行了相关研究与仿真验证。首先介绍了增加障碍物斥力、“绕墙走”方式、自动添加子目标点、手动添加子目标点等4种解决局部极小值的方法；然后分析了人工势场法的缺陷原因，并对人工势场法的局部极小值问题进行了改进；最后进行了仿真实验，结果表明采用人为添加子目标点的方式可以使移动机器人摆脱局部极小值并抵达目标点，并且路径长度短、路径安全性高，是4种方法中最有效的方法。