雷达群目标跟踪条件下的弹道预报方法

杜广洋,郑学合

(1.北京电子工程总体研究所,北京 100854;2.中国航天科工防御技术研究院科技委,北京100854)

0 引 言

在对弹道导弹目标进行跟踪时,一般情况下,在几公里的距离波门内聚集着弹头、诱饵等目标特性不尽相同的分离目标。这些目标大部分有着相近的状态向量(位置和速度),从而形成近距离物体(closely spaced objects,CSOs)[1-4]。如何对CSOs目标进行稳定、准确地跟踪和弹道预报,对于目标识别、信息融合等都具有重要意义。

随着雷达技术的发展,距离高分辨技术越来越多地被采用,对复杂场景下的多目标进行距离分辨和分离目标跟踪成为可能,即群目标跟踪[5-8]。在利用群目标跟踪技术跟踪CSOs情况下,雷达很难对群内所有目标保持稳定跟踪。影响因素可能来自于不同的目标散射特性、不同的受干扰程度、航迹交叉等方面[9]。如果群内有子目标跟踪丢失,则为了维持断续航迹编号、关键事件状态、多雷达交接等应用需求,需要对丢失目标进行航迹维持[10-12]。常用的方法是利用弹道导弹运动轨迹可预测的特点对丢失目标进行弹道预报。由于目标跟踪丢失,弹道预报无法获得观测数据的修正,因此航迹维持的精度主要取决于目标丢失时刻的初值精度,并且随着外推时间的增大而变差。

在进行群目标跟踪时,雷达同时对CSOs中的多个子目标进行同步测量。各个子目标测量信息中的系统误差、杂波和噪声干扰、状态估计的过程噪声等都具有相同或者相似的性质,即群内多子目标探测信息具有相关性[13]。此时,多子目标之间相对误差远小于单个目标绝对误差。因此,挖掘和利用这一特性,用雷达当前跟踪的子目标对其他丢失子目标进行相对弹道外推,对于提高航迹维持的精度具有很强的现实意义。

本文提出了利用群内弹道目标的相对运动关系,用雷达正在跟踪的子目标对其他丢失子目标进行弹道预报的方法。通过误差分析,对比研究了单纯弹道预报与该方法的递推误差特性。仿真表明,当雷达对群目标探测信息相关性较好时,该方法大幅提高了弹道预报精度。

1 常用的弹道预报方法及其误差特性

1.1 单纯弹道预报方法

当雷达跟踪的某个子目标出现跟踪丢失时,一种最常用的航迹维持方法就是利用以该子目标跟踪丢失前某个稳定的跟踪状态为初值,利用弹道运动方程进行外推。

(1)

式中

μ=3.986 004 418×1014(m3/s2)为地球引力常数;ω=7.292 115 14×10-5(rad/s)为地球自转角速度。

如果目标跟踪丢失,并且需要利用弹道预报进行航迹维持,则用四阶四级龙格-库塔法对弹道微分方程式(1)进行数值计算,可以获得足够的递推解算精度[16]。设目标在t时刻运动状态为St,则在t+1时刻(时间间隔为Δt),运动状态St+1可进行递推解算为

(2)

1.2 单纯弹道预报方法的误差分析

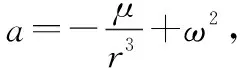
(3)

式中,

St+1≈BSt

(4)

设在k时刻前,雷达跟踪正常,利用持续的观测量Z1,Z2,…,Zk可得在k时刻Sk的最小均方误差估计的协方差矩阵为Pk。若k+1时刻目标跟踪丢失,则其利用式(1)进行外推的预报状态协方差阵Pk+1可表示为(忽略过程噪声)

Pk+1=BPkBT

(5)

若其以Sk为初值利用单纯弹道预报方法进行弹道预报,则递推n步以后状态量为

Sn=BnSk

(6)

则递推n步后的预报状态协方差阵Pn可表示为

Pn=BnPk(BT)n

(7)

由式(7)可见,递推误差以跟踪丢失前状态估计误差Pk为起始呈现逐步放大趋势。

2 群目标跟踪条件下的相对弹道预报方法

在雷达对CSOs中多个弹道目标进行群目标跟踪时,由于具有相似的量测偏移量和过程噪声,群内多子目标间的相对运动状态估计误差要明显优于单个目标的运动状态估计误差。因此,当群内某一子目标跟踪丢失时,若需要利用弹道预报进行航迹维持,可以考虑获取丢失前群内多子目标间的高精度相对运动状态,利用未丢失的其他子目标跟踪航迹用相对弹道预报的方式来维持已丢失子目标的航迹。

2.1 两个弹道目标相对运动模型

设群内两个弹道目标的状态量分别为S1、S2,定义相对运动状态量为ΔS=S2-S1。则在t时刻,相对运动状态ΔSt可表示为

(8)

在两个子目标跟踪存续期,各个子目标建立独立的滤波器维护各自的状态估计值。滤波器可以选取扩展卡尔曼滤波、不敏卡尔曼滤波、多模型等方法[17-20],本文不再赘述。利用式(8)维护一个开环的相对运动状态估计,以备某一子目标跟踪丢失后作为弹道预报的初始值。

2.2 目标跟踪丢失后的航迹维持方法

(9)

图1为子目标2跟踪丢失前的t时刻和子目标2跟踪丢失的t+1时刻两帧的跟踪状态估计过程流程图。

图1 目标跟踪丢失前后的状态估计过程Fig.1 State estimation process before and after target tracking loss

2.3 群目标跟踪条件下的相对弹道预报方法误差分析

(10)

定义B′=B2-B1,则

(11)

(12)

(13)

则递推n步以后子目标2的预报状态协方差阵可表示为

(14)

2.4 利用群内目标间的相对运动关系提高弹道预报精度的机理分析

为描述方便,将常用的单纯弹道预报方法简称为BF-single方法,将本文提出的群目标跟踪条件下的相对弹道预报方法简称为BF-relative方法。

2.4.1 定性分析

假设目标2在k+1时刻以后跟踪丢失,将式(7)与式(14)做差,可得

(15)

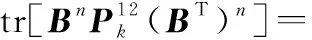
(16)

2.4.2 定量分析

以对高度为500 km的弹道导弹进行弹道预报为例,设雷达对单目标的绝对测量误差为δS0=[200 200 200 20 20 20],相对测量误差δΔS0分别为绝对测量误差δS0的10%、30%、50%和80%几种情况时(即κ分别为0.1、0.3、0.5、0.8),两种预报方法的外推时长与位置预报误差对比如图2所示。

图2 两种预报方法的外推误差对比Fig.2 Comparison of position error between two trajectory prediction methods

由图2可见,两种预报方法的误差大小主要取决于初值时刻绝对误差或相对误差的大小,即相对误差越小则外推误差越小。这恰恰证明了本文讨论问题出发点的正确性。

2.5 群内多个目标时的航迹维持方法

下面将BF-relative方法推广至更一般的群内多个目标情形。

步骤3计算t+1时刻各跟踪目标对丢失目标1的相对运动状态预测值和误差协方差,即

(17)

(18)

步骤4计算t+1时刻各跟踪目标对子目标1的状态估计(即预报值)和误差协方差,即

(19)

(20)

步骤5合成各跟踪目标对子目标1的状态估计,计算t+1时刻子目标1的状态估计和误差协方差[21-22],即

(21)

(22)

对于群内多个子目标跟踪丢失的情形,仍可用上述方法,利用剩余跟踪的航迹维持所有丢失子目标航迹。只要群内还剩余不少于1个子目标跟踪航迹,就能完成对群内所有丢失子目标的预报航迹更新。

3 仿真分析

3.1 仿真条件

(1)两个弹道目标情形

利用典型600 km射程弹道导弹弹头及其分离物的理论弹道,构成由两个弹道目标组成的CSOs。雷达对这两个目标进行群目标跟踪,形成了子目标1和子目标2。前80 s,雷达同时跟踪子目标1和子目标2;80～220 s,雷达丢失子目标2,只跟踪子目标1,在下面3种情况下利用弹道预报生成了子目标2的预报航迹。这3种情况包括:①用BF-single方法,以子目标2在80 s丢失前的状态量为初值进行弹道预报;②用BF-relative方法,用子目标1当前跟踪航迹,通过相对弹道预报维持子目标2航迹,其中,雷达相对误差设定为0.01°;③仍用BF-relative方法,雷达相对误差放大到0.03°。通过仿真检验本文阐述的相对弹道预报方法的有效性。仿真参数如表1所示。

表1 仿真参数Table 1 Simulation parameters

(2)多个弹道目标情形

仍利用典型600 km射程弹道导弹弹头及其分离物的理论弹道,构成由4个弹道目标组成的CSOs。雷达对这4个目标进行群目标跟踪,形成了子目标1～子目标4。前80 s,雷达同时跟踪子目标1～子目标4;80～220 s,雷达丢失子目标1,子目标2～子目标4仍能保持跟踪,在下面两种情况下利用BF-relative方法生成了子目标1的预报航迹。①只用子目标2当前跟踪航迹,通过相对弹道预报维持子目标1航迹;②综合利用子目标2～子目标4当前跟踪航迹,通过相对弹道预报维持子目标1航迹。通过仿真比较检验多个子目标共同维持丢失子目标航迹的精度提升效果。仿真参数与表1一致(其中,雷达相对误差均设定为0.03°)。

3.2 仿真结果分析

通过跟踪航迹位置的均方根误差(root mean square error,RMSE)表征航迹跟踪或预报效果。假设蒙特卡罗试验次数为M,则位置的RMSE可表示为

(1) 两个弹道目标仿真结果分析

作为对比,同时给出以下4种情况位置误差随时间的变化曲线:

①子目标1在0～220 s跟踪位置误差;

②子目标2在0～80 s跟踪位置误差和80～220 s用BF-single方法预报外推的位置误差;

③子目标2在0～80 s跟踪位置误差和80～220 s用BF-relative方法预报外推的位置误差(01号参数:雷达相对角误差0.01°);

④子目标2在0～80 s跟踪位置误差和80～220 s用BF-relative方法预报外推的位置误差(02号参数:雷达相对角误差0.03°)。

仿真结果如图3所示。

图3 4种跟踪位置误差仿真对比结果Fig.3 Simulation results of tracking position error in four cases

仿真结果与误差特性分析的结论是一致的,即当雷达对多目标探测信息相关性较好时,相比于BF-single方法,本文提出的BF-relative方法大幅提高了弹道预报精度。当雷达相对误差较小时(在上述仿真场景下为0.01°,即相对测量误差为绝对测量误差的10%),BF-relative方法得到的目标2预报航迹与目标1的跟踪航迹位置误差基本相当。

(2) 多个弹道目标仿真结果分析

作为对比,同时给出以下两种情况位置误差随时间的变化曲线:

①子目标1在0～80 s跟踪位置误差和80～220 s用2个弹道目标相对关系预报外推的位置误差;

②子目标1在0～80 s跟踪位置误差和80～220 s用4个弹道目标相对关系综合预报外推的位置误差。

仿真结果如图4所示。仿真结果表明,当群内有超过两个子目标时,只要群内还剩余不少于1个子目标跟踪航迹,就能完成对群内所有丢失子目标的预报航迹更新,但相比于利用两个子目标间相对关系维持丢失子目标航迹,用多个子目标共同维持丢失子目标航迹的精度提升效果明显。因此,在计算资源允许时,应尽量选用多个目标合成外推的方法。

图4 两个和4个弹道目标预报位置误差仿真对比结果Fig.4 Simulation results of tracking position error in two and four tracks

4 结 论

提出了空间群目标跟踪条件下的BF-relative方法。本方法挖掘利用了雷达在探测群目标时相对误差一般小于单个目标的绝对误差的特性,通过仿真表明,本方法相比传统单目标BF-relative方法精度大幅提高。

需要说明的是,该方法的基础是该预测的相对误差能较好地作为估计状态相对误差的估计,而这需要有一定前提的,即群目标间不能发生机动运动,一旦其中一个目标存在机动运动,这个相对误差估计结果就是错误的。

通过误差分析,探讨了本方法误差传递机理,同时,也明确了后续进一步提升弹道预报精度的方向。今后的工作是研究进一步提升跟踪存续期群目标间相对精度的实时状态估计方法。