低比度钢板微小缺陷的图像增强和分割
2020-12-24杜绪伟
杜绪伟,陈 东
(青岛科技大学机电工程学院,山东 青岛 266061)
0 引言
钢板在制造过程中,会产生划伤、锈斑、翘皮、和孔洞等表面缺陷。这些表面缺陷不仅影响产品的外观还降低了产品性能。随着科技的进步与经济的发展,人们对钢制工件的需求大大增加,但随之而来的质量要求也越来越严格,所以企业对钢制工件的表面检测越来越重视[1]。钢板图像中的背景、缺陷和噪声等信息都包含在一个较小的灰度范围内,造成图像对比度较低,不易分割。在图像采集过程中,还容易受到光照、钢板自身反射等因素的影响造成图像的灰度不均[2]。并且缺陷部位占的整体面积比例较小,不易分辨,这些都为后续有效地分析和识别缺陷增大了难度。为了克服这些因素以便更好地对缺陷进行识别与分割,本文采用先对图像进行图像增强以突出缺陷信息,并在此基础上进行图像分割,以达到缺陷部位从背景中分割出来的目的。
针对低对比度的常用图像增强方法有灰度变换法、同态滤波法和直方图均衡化法等[3-5]。灰度变换法是通过一定的点运算修改图像的像素灰度来扩展图像的对比度,分为线性灰度变换、非线性灰度变换2大类,非线性变换的增强效果通常比线性的增强效果好,但有变换函数困难、通用性较差等问题;同态滤波法通过映射原有信号转换到线性滤波器的不同域进行运算,运算完成后再映射到原始域,可以去除乘性噪声使亮度变得均匀、细节得到增强,但同态滤波也会带来过增强及对高光区增强效果差的问题;直方图均衡化法是通过扩展输入图像直方图的动态范围来实现增强对比度的功能,这种方法虽然对背景和缺陷都太亮或者太暗的图像效果不错,但是它不仅可能会降低有用信号的对比度,还会增加噪声的对比度。
针对同态滤波增强效果不明显的问题,本文利用小波变换的“变焦”特性使得根据不同的特性得到不同的局部化特征,对低频部分进行光照校正,对高通部分进行高通滤波使微小缺陷从背景中突出[6]。采用小波-同态滤波增强图像后,对其进行图像分割得到缺陷区域,选择一个图像分割方法也尤为重要。常见的Sobel算子、Roberts算子、Prewitt算子和Kirsch算子对低对比度图像的边缘检测效果也并不优异[7-10]。Canny算子目前在边缘检测方面仍然得到广泛的运用,但它的分割效果容易受到阈值的影响[11]。针对这一问题,本文采用粒子群算法优化最大类间方差法(PSO-Otsu)确定最佳阈值,并结合Canny算子进行钢板微小缺陷的分割。
1 图像增强
1.1 同态滤波
同态滤波是一种在频域中将频率过滤和灰度变换结合起来的图像处理方法,在照明不均引起的图像降质方面用得很多。其频域处理的基础是图像的照度反射模型,利用图像的灰度范围的调整减轻动态范围过大和照度不均对图像质量的影响。由于它是将图像中所有的像素都进行了处理, 所以它不仅可以保持较亮区域的信息,还可以增强较暗区域的信息,因此具有全局性。
一般图像f(x,y)可以看做由照射分量i(x,y)和反射分量r(x,y)的乘积表示,即
f(x,y)=i(x,y)·r(x,y)
(1)
0 其中,i(x,y)的频谱在低频区域,r(x,y)的频谱在高频区域。因为照射分量的性质由光照条件来决定,所以其在空间上的变化比较缓慢;反射分量由物体的表面特性来决定,用来反映图像的细节。同态滤波就是为了消除照度不均的影响,并且在保证不损失亮区信息的同时增强暗区的细节信息。由于照射分量和反射分量的乘积是非线性的,所以将式(1)进行对数及傅里叶变换便可得经同态滤波增强后的图像: g(x,y)=exp(i(x,y)+r(x,y))= i0(x,y)r0(x,y) (2) 增强后的照射分量和反射分量分别为i0(x,y),r0(x,y)。同态滤波的流程如图1所示。 图1 同态滤波流程 小波变换是一种新的变换分析方法,作为应用数学和工程学科中一个迅速发展的新领域,小波变换可以覆盖整个频域,同时具有多尺度分析能力,可以极大地减少或去除所提取的不同特征之间的相关性,可以多分辨率地分析信号,在图像处理领域被广泛应用。 由于图像信号一般用二维信号来描述,因此采用二维离散小波来对图像进行分解,根据Mallat快速分解算法,可以将1幅图像f(x,y)表示为 (3) 图2 图像二级小波分解示意 由于低一维的低频系数进行小波分解,分解的结果是某一维的高频系数,通过该维的小波分解又可以得到高一维的小波系数。所以同一维的高频系数的频率高于低频系数,高维高频系数的频率低于低维高频系数的频率。通过低频部分反映了图像的基本面貌,细节特征则可以通过高频部分反映出来。 经同态滤波处理过的图像,虽然可以使亮度得到增强并且得到较均匀的亮度。但由于不能考虑到空域的局部特征,当处理低对比度的微小缺陷图像时,效果并不是很理想。同态滤波算法中,使用傅里叶变换来进行图像处理,但是傅里叶变换的滤波是面对整幅图像的,只能反映频率在信号中的总强度,会删除一些有用信息[12]。与傅里叶变换相比,小波变换能够更加充分地了解频域的各种特性和图像的空间域,并且可以利用空间域和频域的“变焦”特性,根据其不同的分辨率、频率和方向特性得到任一时间域和频率域的局部化特性[13]。将小波变换与同态滤波相结合,便可以利用小波变换的空域和频域的“变焦”特性,对低频成分进行非均匀光照校正,对高频成分进行高通滤波以突出表面缺陷特征。经过在MATLAB 2019b上进行仿真实验,得到该改进算法在图像增强的效果上明显优于经典算法。结合小波变换的同态滤波流程如图3所示。 图3 小波-同态滤波流程 为验证本文缺陷分割算法的优异性,增加了直方图均衡化、线性灰度变化法、非线性灰度变换幂 律法、同态滤波和本文所运用的小波-同态增强方法。不同算法的图像增强效果如图4所示。 图4 不同算法的图像增强 最大类间方差法(Otsu)算法是凭借阈值展开图像分割,通过图像目标与背景之间最大方差的计算进行动态获取来得到最佳阈值[14]。若图像I(x,y)有L个灰度级[0,1,…,L-1],灰度级为i的像素点有ni个,那么像素点的总个数为N=n1+n2+…+nL,则各个灰度值概率pi=ni/N。以阈值k作为界限将图像划分为2个区域:C0为灰度级为[0,1,…,k]的像素组,C1为灰度级为[k+1,…,L-1]的像素组。C0、C1产生的概率和平均值分别为: (4) (5) (6) (7) ω0ω1(μ1-μT)2 (8) 粒子群算法是一种模仿鸟群的觅食行为的算法[15]。在粒子群算法中,每个优化问题的潜在解都被看做为粒子,使其在约束条件下进行自动寻优。它的基本原理如下所述。 假设在1个D维空间的求解空间中,有N个粒子组成的1个群落,算法要做的就是在D维空间中通过更新速度和位置来逐步逼近最优解。其中,第i个粒子表示为1个D维向量Xi=(xi1,xi2,…,xiD);第i个粒子的速度为Vi=(vi1,vi2,…,viD);第i个粒子能搜索到的最优个体位置记为Pbest=(pbesti1,…,pbestiD);整个粒子群能搜到的最佳全局位置记为Gbest=(gbesti1,…,gbestiD),i=1,2,…,N。粒子群体根据式(9)和式(10)更新自己速度和位置。 vid=ω·vid+c1r1(pid-xid)+c2r2(pgd-xid) (9) xid=xid+vid (10) c1和c2为学习因子;r1和r2为[0,1]之间的均匀随机数。 粒子群优化最大类间方差法(PSO-Otsu)是利用PSO在Otsu的基础上进行最佳的阈值搜索,得到最佳的阈值后结合Otsu分割图像,执行过程如图5所示。由Otsu算法的分割过程可知,其算法本质就是找到1个可以得到最大值的灰度值t。由于原始算法存在计算量大、耗时多等问题,本文将PSO算法应用在Otsu中,利用Otsu里的各个参数匹配到PSO算法里来进行迭代。将类间方差σ2作为PSO的适应度函数,阈值更新速度作为粒子的飞行速度,在PSO中搜索可以使σ2得到最大值的灰度值。 图5 PSO-Otsu算法流程 由于Otsu法对噪声和目标物的大小比较敏感,对于对比度较低的工件进行图像分割时,单一使用Otsu法难以取得较好的结果[16]。Canny算子在抗噪声和边缘精确定位方面效果较好,Canny算法采用高斯函数滤波器来平滑图像,并对图像矩阵执行卷积运算,实现图像的消除噪声和平滑处理[17]。高斯函数的表达式为 (11) 平滑后的图像表达式I(x,y)为 I(x,y)=G(x,y)·f(x,y) (12) f(x,y)为原图像的函数;σ为高斯滤波器分布参数。 Canny算法利用2×2的模板来计算图像梯度。用X、Y方向像素的一阶偏导来确定图像的梯度和幅值。 用X、Y方向的偏导数分别与图像f(x,y)进行卷积运算,得到输出公式: (13) (14) 令A(i,j)和ϑ(i,j)来代表点(i,j)处的梯度幅值和方向,则梯度幅值为 (15) 梯度方向为 (16) 由于Canny算子是在2×2的邻域内进行计算,处理对比度较低的工件时对噪声过于敏感,导致容易丢失边缘信息并且易增加过多干扰信息[18]。所以本文利用基于小波变换的同态滤波对图像进行预处理,以提高图像对比度,使缺陷部分和背景的区分更加明显。 在处理图像过程中,需要分割的缺陷目标和背景的大小差异性过大,并且受到光照及其他外部条件的影响,直接用Canny算法检测时,分割效果并不优异。当阈值过高时在清除噪声的过程中会过度清除掉图像的边缘信息和漏掉微小缺陷信息;当阈值过低时,检测会受到噪声的干扰,故利用PSO-Otsu得到的阈值作为Canny算子的高阈值来检测缺陷边缘,避免因为阈值过低、过高造成的影响。 钢板表面缺陷视觉检测系统主要由硬件系统和软件系统组成。硬件系统主要由1台线阵CMOS相机、1个LED光源、工业计算机和编码器组成。系统结构如图6所示。其中,LED光源将被测钢板表面照亮,编码器触发线阵CMOS相机采集钢板的表面图像,系统根据采集到的图像对相机的曝光时间进行调节,保证图像灰度值的均匀性。 图6 图像检测系统结构 系统使用相机型号为DALSA P4-CM-08K070工业线阵CMOS相机。该相机的分辨率为8 192×2,像元尺寸为7.04 μm×7.04 μm,最高频率为140 kHz,本系统选用了50 mm的镜头。由1.3节可知,本文选择的小波-同态图像增强算法可以有效地增强工件的低对比度问题,所以采用图像增强后的结果图来进行图像分割。图7和图8分别为图像增强前和增强后的缺陷检测,并对比了Otsu阈值法、Canny算子和本文PSO-Otsu优化阈值的改进Canny算法的检测结果。 图7 图像增强前的缺陷检测 图8 小波-同态滤波算法增强后的缺陷检测 由图7和图8可知,Otsu阈值法在图像增强前和图像增强后都不能有效地把缺陷和背景分离出来;传统Canny算子由于没有找到合适的阈值造成缺陷被噪声所淹没。所以在处理低对比度的图像时,Otsu阈值法和传统Canny算子都不能有效地解决图像分割问题。为了进一步校对对比度是否增强对于图像分割的影响,截取图7和图8的缺陷区域进行对比得图9。 图9 细节对比 对比图9b和图9c可知,本文算法可以将缺陷有效地分割出来,但是未经小波-同态滤波增强的分割图像虽然被检测出来,但图像封闭性较差。经过小波-同态增强后的图像缺陷的细节信息更加明显且图像的封闭性较好。为验证小波-同态滤波后的图像分割效果,增加2组图像进行对比试验如图10和图11所示。 由图10和图11可知,本文算法无论图像增强与否,都可以将缺陷从背景中分离出来,但是经过小波-同态滤波进行对比度增强之后的图像分割,可以得到的缺陷细节信息更加丰富,缺陷轮廓也更加封闭。 图10 第1组分割对比 图11 第2组分割对比 当处理低对比度工件的表面微小缺陷时,不进行图像预处理,直接运用Otsu、Canny算子和本文的改进分割算法等图像分割方法,都不能使缺陷和背景及噪声有效的分离。当对图像进行小波-同态图像增强后增强了图像对比度,传统Otsu算法虽然处理一般图像时具有良好的分割效果,但当缺陷较小时并不能有效地将缺陷和背景进行分离;传统的Canny算子由于固定的双阈值,适应性不强,其2×2的邻域模板会对噪音比较敏感,容易丢失边缘信息且易增加过多干扰信息,致使检测精度过低。 运用PSO-Otsu结合Canny算法可以使微小的缺陷和背景有较好的分离效果,也避免被噪声干扰的问题,对低对比度工件的微小缺陷检测具有较好的效果。本文的下一步工作主要是针对分割出的微小缺陷进行识别,利用机器学习方法完成对缺陷的分类和评级。
1.2 小波变换


1.3 特征提取


2 表面缺陷分割
2.1 最大类间方差法
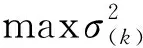
2.2 PSO-Otsu算法

2.3 Canny边缘检测算法

2.4 融合算法
3 实验结果及分析






4 结束语
