基于人工智能算法的电力系统无功优化调度研究

彭嘉宁

(国网宁夏电力公司调度控制中心，宁夏 银川 750001)

0 引言

随着电网的发展，智能电力调度技术越来越重要，其中，发电机组的启停问题是影响电力调度平衡和优化的重要因素。电力系统需要为各种负载需求、电力供应、传输和分配提供稳定服务，也是可再生能源系统的核心。可再生能源的逐渐增加提升了电力调度的难度，而电力的不合理和不可控分配增加了电力传输损耗，降低了电力质量，因此智能、可靠的电力调度技术具有重要意义。

电力调度过程中，最优无功功率分配(ORPD)受到的关注日益增多，因为它对于电力系统的安全和经济运行起着重要作用。ORPD是最优潮流(OPF)计算中的一种特殊形式，是电力系统中的典型非线性和非凸优化问题，涉及离散和连续控制变量，同时满足各种平衡和不平衡约束[1-4]。

在提高电力系统运行中应用ORPD的主要目的，是在系统中重新分配无功功率，以实现总传输损耗的最小化和提高电压分布均匀性[3,5]。因此为了最小化传输损耗和其他目标函数，需要确定所有可控变量的最佳可能组合，其中就包括变压器抽头比率、发电机母线电压和无功补偿器尺寸等。

为此，本文提出了一种自然启发式的人工智能算法，即飞蛾-火焰优化(MFO)算法来解决ORPD问题。优化计算的总体目标是使系统的总传输线损达到最小化。通过IEEE-30总线系统对本文提出的优化算法进行了仿真计算，并且对比了其他几种优化算法的优化效果，从而验证了所提算法的有效性。

1 数学模型

潮流最优化问题(OPF)研究是一种对电力系统中电力潮流进行分析的方法。其主要内容是对电力系统中连接的负载供电能力，以及满足客户电力需求的能力进行分析。 OPF研究对于现代电力系统的最佳运行方式，以及规划电网的未来发展至关重要。通常OPF问题可定义为具有大规模、高约束度、高非线性和非凸特征的优化问题[2-6]。优化涉及的各种目标包括最小化发电成本、最优无功分配(ORPD)、VAR投资成本和社会效益最大化等[7]。 在OPF方法[8]中，通过使用优化技术[9]寻找最优解并平衡潮流方程。

1.1 无功调度最优化模型

ORPD是OPF计算的一个子问题。它被定义为电力系统中的一个非线性优化问题，既包含连续的控制变量又包含离散的控制变量，同时又满足物理和运行约束[4]。 ORPD的主要目标是通过重新分配电力系统中的无功功率来最大程度地降低功率损耗，改善电压曲线和电压稳定性[10]。目前，针对ORPD问题，研究人员开发了各种优化技术对不同优化目标进行优化。本文着重考虑了功率损耗的最小化，其目标(目标函数)是在满足电力需求的同时最大程度地降低电力传输损耗和电力系统的电压偏差， 问题可以表示为求函数f(x，u)的最小值，即

min[f(x,u)]=min(g(x,u),h(x,u))

(1)

g(x,u)=0

h(x,u)≤0

f(x,u)为目标函数；g(x,u)=0为等式约束(潮流等式)；h(x,u)≤0为不等式约束。

不平等约束包括发电机母线电压、变压器抽头比率和无功补偿器的数量；各种约束函数中的x和u分别是函数因变量和控制变量。ORPD的目标是使系统总传输损耗F最小[4-11]，即

2ViVjcos(θi-θj))

(2)

NL为传输线号；gk为第k条线路；Vi和Vj分别为第k条线路的总线i和总线j末端的电压；θi和θj分别为线路i和j端的角标号。

1.2 约束模型

1.2.1 功率平衡约束

采用等式进行约束的是功率平衡方程，要求潮流的功率相等，即总功率损耗等于总发电量减去总负载需求[11]。该等式约束如下：

(3)

(4)

Vi和Vj分别为负载母线i和母线j的电压；Bij为总线i与总线j之间的电纳；Gij为总线i与总线j之间的电导；PGi和QGi分别为有功功率和无功功率；PDi和QDi分别为实际负载需求和无功负载需求。

1.2.2 不平衡约束

在ORPD问题中，不平衡约束主要涉及发电机、变压器和电抗设备的约束。如前所述，ORPD是一个包含连续和离散参数的问题。为了分析离散变量，在优化开始时先将其视为连续变量，优化的最后再连续变量映射回其对应的离散值。所有不平衡约束都受到其上下边界的限制，这样才能获得稳定的求解结果。发电机的约束条件包括有功功率、无功功率和母线电压，它们的上下限为：

(5)

(6)

(7)

i=1,…,NG，NG为发电机的数量。

变压器抽头分接比的范围限制为

(8)

i=1,…,NT，NT为变压器的数量。

无功补偿器的尺寸限制为

(9)

i=1,…,NC，NC为无功补偿器的数量。

1.2.3 惩罚约束

ORPD作为一个约束优化问题，主要包括有发电机母线电压、变压器分接比和无功补偿器的尺寸等不等式约束，而利用MATPOWER[12]可以自动满足本研究中的等式约束(幂平衡方程)。因此，通过将总线PQ的电压幅度以及注入总线PV的无功发电作为目标函数的惩罚项，就可以对母线电压和无功功率加以约束[13-15]。以上问题可以由表示为

(10)

(11)

如果控制参数超出限制范围，则应将惩罚函数纳入目标函数；另一方面，当所有控制参数都在其边界范围内时，惩罚函数等于0。在本文研究中，惩罚因子设置为100 000，由于惩罚因子的值很大，并且持续增加直到接近无穷大，此时受约束ORPD问题将转换为无约束ORPD问题。

1.3 MOTH-FLAME优化模型

MOTH-FLAME(飞蛾趋火)优化算法是[5]自然启发式人工智能优化算法，与其他优化算法相比具有一定优势。MFO算法的灵感来源于飞蛾在夜间的独特导航机制：飞蛾在夜间航行时利用了一种称为横向定向的机制，该机制取决于月光，在自然界中由于月球距离飞蛾相对较远，飞蛾沿横向直线运动，可见这种机制仅在光源非常远的情况下对于直线行进有用。但是实际上飞蛾容易受到人造光源的误导，导致其围绕光源螺旋飞舞。在MFO模型中，飞蛾在搜索区域中的位置是优化问题的变量，MFO算法本质上是一种粒子群算法，为了对该算法进行建模，第1个重要部分是在矩阵中表示的飞蛾种群的集合，即

(12)

n为飞蛾的种群数量；d为变量的维数。MFO的第2个重要部分是表示火焰数量的矩阵，即

(13)

n和d分别为飞蛾的数量和维数。该矩阵可存储到目前为止获得的n个最相近的最优解，在优化过程中飞蛾必须根据此矩阵更新空间位置，因此计算过程中基于矩阵F中的火焰来定义飞蛾的下一个空间位置。 由于式(12)和式(13)的维数相等，因此可以假设存在一个用于存储飞蛾和火焰适应度值的数组，即

(14)

(15)

OM和OF分别为存储飞蛾和火焰适应度值的数组；n为飞蛾的种群数量。适应度值是每个飞蛾和每个火焰分配的目标函数的返回值或输出值。

飞蛾和火焰都可以作为优化问题的解决方案，但是二者在处理和更新方面截然不同。在MFO中火焰坐标是当前求解步下飞蛾的最佳位置，而飞蛾是搜索区域中的实际搜索者。因此在搜索区域进行搜索时，火焰可以看作是飞蛾掉落的标志，而每个飞蛾都会在火焰周围搜寻并更新其位置以找到更好的结果。这种机制有助于在搜索解的过程中不遗失最佳解决方案。上述过程可以通过式(16)进行建模[5]：

Mi=S(Mi,Fj)

(16)

Mi和Fj分别为第i个蛾和第j个火焰；S为螺旋函数。

通过以下数学表达式建模，该螺旋函数是飞蛾空间位置更新的主要机制：

S(Mi,Fj)=Di·ebt·cos(2πt)+Fj

(17)

b为用于定义对数螺旋形状的常数；t为在[-1,1]区间内的随机数；i为下一个飞蛾离火焰的距离。

为了避免求解陷入局部最优，飞蛾只能利用式 (17)中的一个火焰来更新其位置。Di表示第j个火焰与第i个飞蛾的距离，即

Di=|Fj-Mi|

(18)

Fj为第j个火焰；Mi为第i个飞蛾。

该算法的主要组成部分是飞蛾的螺旋运动方程，它决定了飞蛾在火焰周围更新位置的方式。由于式(17)允许飞蛾绕火焰螺旋飞行，而基本上不在飞蛾之间飞行，因此该方程可确保实现自动寻解过程。当飞蛾的下一个位置位于火焰和飞蛾之间的区域之外时，算法就会自动搜索飞蛾位于火焰和飞蛾之间的区域位置。

更新火焰列表后，算法根据每次迭代的适应度对火焰进行分类和排列。然后飞蛾根据其对应的火焰再进一步更新位置，此外假设在迭代的初始阶段，存在有N个火焰，但是火焰的数量将在迭代过程中逐渐减少。因此在迭代的最后阶段，飞蛾只根据适应度更新位置以寻求位置最优解。火焰数量的减少有助于平衡搜索区域的计算成本[5]，描述此过程的火焰数可表示为

(19)

N为最大火焰数；l为当前的迭代次数；T为最大迭代次数。

解决ORPD问题所采用的MFO算法流程如图1所示。图1中，虚线框表示利用MFO算法解决ORPD问题的主要求解过程。

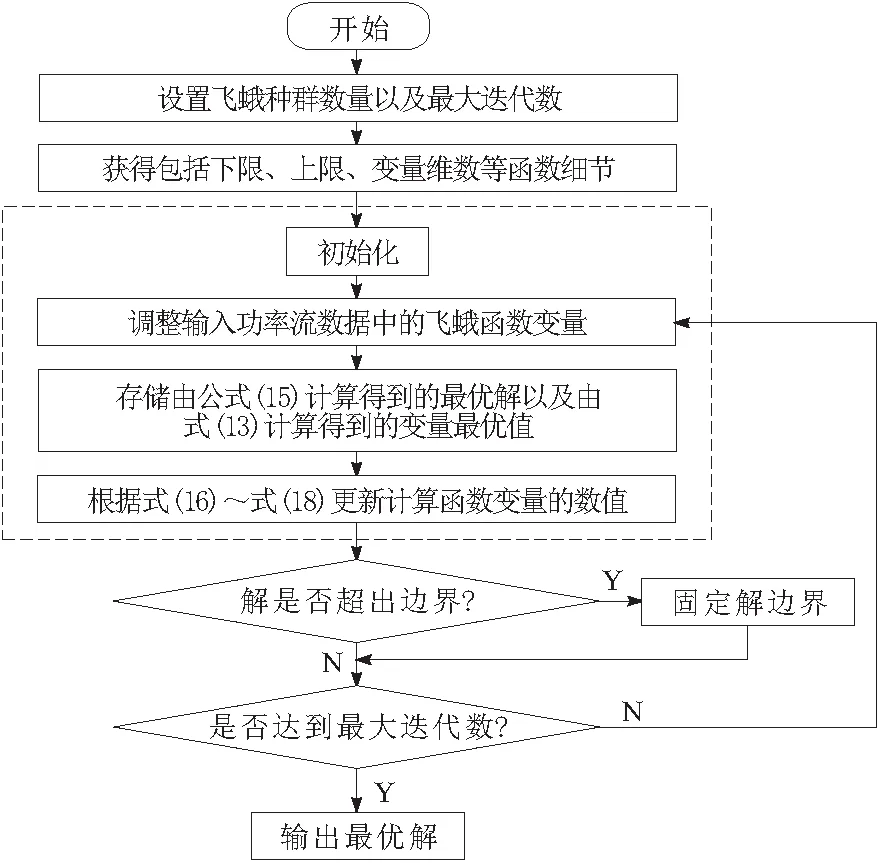
图1 利用本文方法求解最优调度问题的流程

MFO算法在解决ORPD问题时，通过找到控制变量的最佳设置来最小化目标函数，同时需要满足等式和不等式约束。MFO算法是基于种群的算法，在种群数量矩阵(式12)中，矩阵的行表示飞蛾，列表示控制变量(飞蛾的位置)。在计算过程中，每个飞蛾的位置都将映射至潮流数据中。然后执行潮流计算程序以获得系统传输损耗。在每次迭代过程中飞蛾根据其对应的火焰不断更新位置(式15～式17)。然后根据解决方案的适应度对解决方案进行分类和排列，并以矩阵形式保存。因此最优的解决方案将位于矩阵的上部，而最差的解决方案将位于矩阵的下部。

此外，算法还将检查控制变量是否超出约束范围，如果控制变量超出范围，则会在上下边界处进行标记，以确保获得的结果是准确的。MFO算法持续计算该过程，直到计算达到预定义的停止条件(最大迭代次数)为止。此外，每个负载母线的电压幅度必须在指定的范围内，如本研究中使用的母线电压的波动幅度是±10%。

2 计算仿真结果与讨论

为了说明MFO算法在解决ORPD问题上的有效性，本文使用IEEE-30总线系统，并考虑了25个控制变量。MFO算法和其他算法计算得出的最优传输损耗之间的比较如表1所示。

表1 不同算法情况下功率损失百分比计算值对比

由表1可知，本文提出的MFO算法的最小传输功率损耗为PLoss= 2.830 MW，大约减少了50.76%的传输损耗，表明MFO算法性能优于ALO 算法[16]、MVO 算法[17-18]和GWO 算法[4,19]，验证了MFO算法的有效性。

出于方便比较目的，本文将MFO算法的仿真参数以及其他比较算法的最大迭代次数设置为30。MFO算法经过30次自由迭代运行仿真的性能特性曲线如图2所示。根据图2，MFO算法在最佳、平均和最差解决方案3种情况下，算得的传输损失分别为2.830 MW，2.891 MW和3.127 MW，可知通过MFO算法获得的大多数调度方案的传输损失区间范围为2.800～3.150 MW。

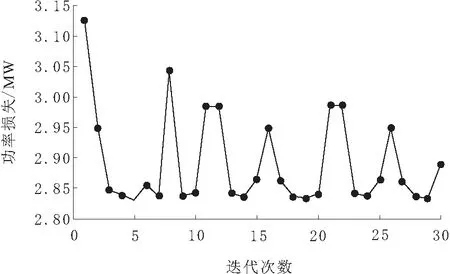
图2 MFO算法的性能特性曲线

3 结束语

提出了一种MFO算法，并在IEEE-30总线系统上进行了测试。根据实验结果，可以得知MFO算法比其他选定的算法优越。在将来的工作中可以将MFO算法实施到其他OPF问题中。