基于离散裂缝模型的CO2增强型地热系统THM耦合数值模拟
2020-12-24孙致学姜传胤任小庆
孙致学, 姜传胤, 张 凯, 庄 丽, 任小庆, 王 强
(1.中国石油大学(华东)石油工程学院,山东青岛 266580; 2.韩国建设技术研究院极限环境研究中心,韩国高阳 10223; 3.陕西绿源地热能开发有限公司,陕西咸阳 712000; 4.国家地热能源开发利用研究及应用技术推广中心,北京 100083)
增强型地热系统(enhanced or engineered geothermal system,EGS)是目前干热岩能源开发工程的关键技术,至今已有40多年的研究历史[1-2]。EGS通过采取水力压裂等工程手段在地下深处的干热岩体中形成载热工质流动通道,利用低温流体与高温岩体的热交换实现深部干热岩热能的提取与利用[3-4]。近年来,为应对二氧化碳减排需求,以二氧化碳为载热工质的新型增强型地热系统(CO2-EGS)受到广泛关注。Brown[5]首次提出使用CO2作为增强型地热系统载热工质,该技术可以在二氧化碳地质储存的同时带来了附加效益; Pruess等[6-9]定量对比了CO2和水的热物理性质,并应用数值模拟方法从流体动力学和传热学角度分析了CO2作为载热工质的优点。除此之外,EGS开发涉及到复杂的传热-渗流-应力(THM)相互耦合作用,导致岩体裂缝的渗透性发生时空动态演化,进而影响整个系统的运行寿命及采热效率[10-11]。前人针对干热岩开采过程中的多物理场耦合问题已经开展了大量研究。Lei等[12]和Rutqvist[13]使用TOUGH2软件模拟了由流体运动和压力变化引起的地层形变,对地热开发中THM耦合问题进行初探。Rinaldi等[14]使用TOUGH-FLAC模拟器分析了多孔介质中人工诱导裂缝和天然裂缝对储层渗透性的影响。Zhao等[15]建立了简化的三维THM耦合数值模型来模拟干热岩的热采过程。然而,上述研究对裂缝特征参数进行了均质等效,难以体现出裂缝系统密度、产状及空间连通关系对载热工质的热交换效果的影响。通过前期研究,形成了深部高温岩体离散裂缝建模方法,并基于此构建了复杂裂缝模型下水-EGS多物理场耦合数学模型及数值求解方法[16]。笔者基于分形几何原理,探究不同裂缝空间拓扑结构以及注采参数对裂缝系统内CO2传质传热以及岩石形变物理过程的影响,并采用一定出口温度下的热采收率对开采效果以及开采寿命进行定量评价。
1 增强型地热系统离散裂缝模型构建
与沉积岩不同,高温结晶岩体基岩原生孔、渗极低,岩体内部原生天然及人工压裂裂缝是载热流体对流换热发生的场所。因此裂缝空间拓扑结构的显式表征是准确模拟CO2-EGS开采动态,预测采热效率及运行寿命的重要基础。离散裂缝模型能够较精确地描述裂缝储层的各向异性以及裂缝与基质的传质传热过程,对于增强型地热系统的开发数值模拟具有先天优势。更近一步地,实际地热储层的裂缝网络会展现出分形特征,裂缝长度和密度发育各不相同,不同裂缝长度和裂缝密度的组合会产生不同的裂缝网络连通性[18-21]。分形裂缝网络的裂缝长度分布通常采用幂律分布模型,裂缝数量与长度的关系[22]表示为
n(l,L)=αLDl-a,l∈[lmin,lmax].
(1)
式中,L为域的大小,m;l为裂缝长度,m;n(l,L)为边长为L的正方形盒子内裂缝长度l在[l,l+dl] (dl≪l)内的裂缝数量;D为分形维数;a为裂缝长度指数;α为与裂缝密度相关的常数;lmax和lmin分别为正方形盒子内裂缝长度的最大值和最小值,m。
裂缝密度I和裂缝穿透系数P的计算式分别为
(2)
(3)
式中,I为裂缝密度,m-1;P为裂缝穿透系数;l′为在面积为AL=L2的范围内裂缝的长度。
P越大代表裂缝网络的连通性越好,通常当P超过一个穿透门限值Pc(Pc≈ 5.8)时,裂缝网络左右两边界之间开始形成贯通的流动通道[19]。本文中的裂缝网络在L=10 m的正方形域内生成。裂缝长度界限为lmin=L/50=0.2 m 和lmax=50L=500 m。裂缝生成时,方向和位置随机,即分形维数D=2。同时,本次研究考虑了5种不同的裂缝长度指数,即a为1.5, 2.0, 2.5, 3.0 和 3.5,以及2种不同的裂缝强度,即I为2.5和5.0 m-1。并且对于每种a和I的组合,随机重复生成10次。图1为不同特征参数下10次重复中的一个裂缝网络示例。可以看出当a很小时,系统被大量的长裂缝占据;当a很大时,系统中主要分布小裂缝。统计结果表明:当P取30.6、16.0、15.5、7.4时,裂缝网络全部贯通;当P=6.5时,有50%的裂缝网络贯通;当P=3.2时,有10%的裂缝贯通;其余参数下的裂缝,全部不贯通。

图1 不同特征参数下的裂缝网络示例Fig.1 Examples of fracture networks with different characteristic parameters
2 CO2-EGS的THM耦合数学模型
2.1 基本假设
在模拟的过程中,假设:①基质和裂缝均视为多孔介质,二者的流动均遵循达西定律,但基质的渗透率和孔隙度远小于裂缝,因此基质内流体流量可以忽略,应力对基质的渗透率和孔隙度的影响也可以忽略;②由于储层压力为75~76 MPa,温度为20~200 ℃,CO2受高压作用,不可能被汽化,假设模拟期间保持单相[6];③由于基质内流体流量可以忽略,因此基质只考虑热传导效应,而裂缝中流体与基质的热交换通过热传导和热对流进行,裂缝流体与基岩的热交换服从牛顿冷却定律;④为简化计算,认为岩体及裂缝始终处于弹性状态,并且基于小变形假设。
2.2 耦合模型控制方程
本文中所涉及的数学控制方程可参考前期的工作[16-17],整个THM全耦合模型由渗流场、温度场、应力场组成,并通过耦合方程建立多场之间的耦合关系。
2.2.1 渗流场控制方程
在基质中,基于达西定律,在饱和流体的弹性多孔介质中,流体的质量守恒方程满足:
(4)
式中,S为储水系数,Pa-1;p为孔隙压力,Pa;κ为基质渗透率,m2;μ为流体黏度,Pa·s;e为岩块的体积应变;Q为源项,m3/s;t为时间,s。
在裂缝中,流体的质量守恒方程为
(5)
式中,df为裂缝开度,mm;κf为裂缝渗透率,m2;ef为裂隙面的体积应变;Qf为基质和裂缝间的交换项,m3/s;τ为沿裂隙切向求导。
2.2.2 温度场控制方程
基质的温度场控制方程为
(6)
式中,Cs为基质岩石的比热容,J/(m3·K);ρs为基质岩石密度,kg/m3;Ts为基质岩石温度,K;λs为基质岩石的导热率,W/(m·K);W为热源项,W/m2。
裂缝的温度场控制方程[23]为
(7)
式中,Tf为裂缝中流体温度,K;ρf为流体密度,kg/m3;Cf为流体的比热容,J/(m3·K);λf为流体的导热率,W/(m·K);h为换热系数,W/(m2·K);uf为裂缝内流体流速,m/s。
2.2.3 应力和位移场控制方程
基质的应力和位移场控制方程[15]为
σij,j+Fi=0,
(8)
μui,jj+(λ+μ)uj,ji-αBpi-βTTs,i+fi=0.
(9)
其中
μ=E/2(1+v),λ=Ev/[(1+v)(1-2v)],
βT=αTE/(1-2v).
式中,σij,j为应力二阶张量分量,Pa;u为位移,m;Fi为体力,Pa;μ与λ为拉梅常数;E为弹性模量,Pa;v为泊松比;p为流体压力,Pa;αB为Biot耦合系数,αB≤1;βT为热膨胀因子;αT为热膨胀系数,K-1;αBpi和βTTs,i分别为水压力作用项和温度应力作用项。
裂缝变形方程[15]为
(10)
(11)

2.2.4 耦合作用
(1)裂缝面渗流与应力的耦合特性。应力场的变化对裂缝的渗透率产生极大影响,而裂缝作为主要的渗流通道,其渗透率的变化对系统换热尤为重要。Louis[24]利用岩体钻孔压水试验对单裂缝面渗流与应力的关系提出了指数型的经验公式为
(12)
其中

(2)流体渗流-热力耦合特性。在不同压力和温度下,CO2的密度和黏度不同,相关数据可由CMGwinprop相态模拟软件计算得出[25]。CO2的比热容随温度变化的关系[26]为
CCO2=1 759.8+7.4T-0.05T2.
(13)
式中,CCO2为CO2的比热容,J/(kg·℃);T为温度,℃。
3 计算参数及条件
3.1 初始及边界条件
渗流场上,设置左边界为注入端,右边界为采出端,并考虑3种不同的压力梯度,具体方式为保持出口压力为75.00 MPa,入口压力(pin)分别取75.01、75.10 和76.00 MPa。上下边界为不渗透边界。储层及储层内部CO2的初始温度均为200 ℃,注入端水温为20 ℃,外边界为热绝缘。模型四周均为固定约束,不考虑原始地应力的影响,仅研究流体压力和温度变化对地应力场的扰动。
3.2 计算参数
设定计算模型尺寸为10 m×10 m,由于基质的渗透率和孔隙度极低,因此不考虑地层弹性的影响,即裂缝和基质的储水率S设置为0 Pa-1。模拟时其他参数[16]:CO2的导热系数为0 W/(m·K);基质密度为2 700 kg/m3,渗透率为1×10-18m2,弹性模量为30 GPa,泊松比为0.25,比热容为1 000 J/(kg·K),导热系数为3 W/(m·K),热膨胀系数为2×10-6K-1,孔隙率为0.000 1;裂缝宽度为0.05 mm,裂缝初始渗透率由立方定律得出,法向刚度为1 200 GPa/m,切向刚度为400 GPa/m,Biot耦合系数为1.0,换热系数为3 000 W/(m2·K)。为了便于分析,将裂缝面渗流与应力影响系数α简单取为0.2×10-8Pa-1。
大量模型算例基于COMSOL Multiphysics with MATLAB统一进行有限元瞬态数值模拟求解,为保证计算的所有模型达到稳态(即储层热量耗尽),设计模拟的总时长为109s。
4 结果讨论
4.1 岩石温度场分布对比
图2为图1中部分裂缝网络在不同注入压力下5×105s (≈5.79 d)时的温度场分布。当岩石内部没有形成贯通裂缝时,岩石内部温度变化主要由基质热传递导致,低温前缘均匀推进。当岩石内部形成贯通裂缝时,低温CO2流体从岩石左端进入,沿裂缝与基质热量交换,变成高温流体从裂缝出口产出。随着注入压力的升高,冷锋前缘的突破速度加快。同时,可以看出裂缝连通性好的网络热波及程度越大。
4.2 岩石等效渗透率变化及对比
等效渗透率能够有效地表征岩石整体的渗透性,是影响采热效率的重要因素。等效渗透率的计算基于达西定律,可表示为
(14)

如果岩石内部未形成贯通的流动通道,岩石的等效渗透率则接近基质渗透率,与内部的孤立裂缝的渗透率无关。在开发过程中,注入流体的压力作用以及岩石的热膨胀效应使裂缝受到拉应力而扩张,裂缝渗透率增大,最终使岩石整体等效渗透率呈上升的趋势。为探究CO2-EGS开发全过程的岩石渗透性变化,针对图1所示的裂缝网络,绘制了不同注入压力下岩石等效渗透率在模拟时间内的变化,如图3所示。可以看出,不同特征参数的裂缝网络在模拟时间内等效渗透率均趋于定值,达到稳态。生产压差越大,达到稳态的时间越短,但是在稳态时岩石的等效渗透率峰值基本不变。这说明在本次模拟中,注入压力变化对岩石等效渗透率的影响非常微小。

图2 不同特征参数下5×105 s时的温度场分布Fig.2 Temperature distributions of cases with different characteristic parameters at t=5×105 s
图4为pin=76.00 MPa时,终止模拟时刻和起始模拟时刻岩石等效渗透率与穿透系数关系的对比。裂缝网络的裂缝密度I越大或长度指数a越小,穿透系数P越大。图4中的岩石等效渗透率与穿透系数呈良好的正相关关系。当裂缝网络未形成贯穿通道时(P

图4 pin = 76.00 MPa时岩石等效渗透率与穿透系数的关系Fig.4 Relationship between equivalent permeability and percolation parameter at pin = 76.00 MPa
4.3 岩石出口温度和热采收率变化及对比
地热资源虽然被认为是可再生资源,但一般经过约20~30 a开采后,EGS地层中储存的能量会急剧减少,这需要相当长的时间恢复[27]。一些研究指出停止系统运作的最佳时间可以为储层平均温度下降10 ℃时[28],或生产温度下降10%[29]。因此评价岩石出口温度和热采收率变化是评价EGS运行寿命的重要指标。
岩石出口温度[30-31]及热采收率[32]计算式分别为
(15)
(16)
式中,Ts和Tf分别为出口基质和裂缝的流体温度,K;uf和um分别为出口基质和裂缝的流速,m/s;加和项为裂缝,积分项为基质岩块;γ为热采收率;T0和Tinj分别为岩石初始温度和注入流体温度,K;Ts(t)为t时刻的岩石温度,K;S为岩石域面积,m2。
首先,仍然对图1中的10个裂缝网络示例在整个开发过程中的参数变化进行对比。图5、6分别为不同注入压力下,出口温度和热采收率在模拟时间内的变化。当岩石未贯通时,出口温度和热采收率不随生产压差的变化而变化。此时,岩石的温度分布主要由基质的热传递决定。当岩石贯通时,裂缝内的CO2流体与基质的对流换热加速了对基质热量的抽取,生产压差增大使冷锋面的行进速度加快,出口温度开始下降的时间提前。对于流动通道较少的岩石,当采用较高的压差开采时,冷锋面迅速向井底突破,出口温度先快速下降,此后缓慢下降至入口温度,产生长尾效应[33],例如P=3.2或P=6.5的岩石。此外,可以看出岩石内孤立的裂缝虽然对等效渗透率变化有所扰动,但是对于地热开发的关键时期(T> 180 ℃)影响很小。
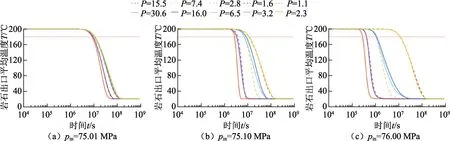
图5 不同注入压力下裂缝网络在模拟时间内出口温度变化Fig.5 Variation of average outlet temperature during simulation time for fracture networks under different injection pressures
为了更好地研究不同裂缝网络对生产压差的响应情况,绘制岩石出口温度随热采收率的变化曲线(图7)。同一出口温度对应的热采收率越大说明岩石的采热效果越好,换热效率越高。从图7中可以看出,穿透系数比较高的岩石(P=30.6),在较高的生产压差下仍在热量抽取40%后出口温度才开始下降。相反,在穿透系数较小的岩石(P=3.2或P=6.5),当pin=76.00 MPa时,在系统热量被抽取约14%时便开始下降。为了进一步探究岩石裂缝几何分布和生产压差之间的相互作用关系,取出口温度为180 ℃时的热采收率(γT=180 ℃)对全部的裂缝网络进行讨论,如图8所示。当裂缝网络未贯通时,出口温度为180 ℃时岩石的热采收率维持在约41%不变,因为此时热传递完全依靠基质传导。当裂缝网络贯通时,系统的热波及效果随穿透系数P(或岩石渗透性)的增加而增加。连通性较好的裂缝网络随着生产压差的增大,γT=180 ℃先升高再降低。但是穿透系数位于Pc周围的裂缝网络未有明显的上升,反而在高压差下γT=180 ℃很低。这是由于增大生产压差一方面可以增大流量,使CO2携带更多的热量,升高γT=180 ℃;另一方面加快了冷锋前缘的推进速度,使γT=180 ℃降低。裂缝强度和连通性较高的岩石能比较充分地利用岩石热量,可以在高流量下仍保持较高的热波及;然而对于裂缝强度和连通性较低的岩石,裂缝网络控制面积低,升高压差会导致注入冷水快速突破,开发效果差。

图6 不同注入压力下裂缝网络在模拟时间内热采收率变化Fig.6 Variation of overall heat recovery with time for fracture networks under different injection pressures

图7 不同注入压力下裂缝网络出口温度随热采收率变化Fig.7 Variation of average outlet temperature with overall heat recovery for fracture networks under different injection pressures
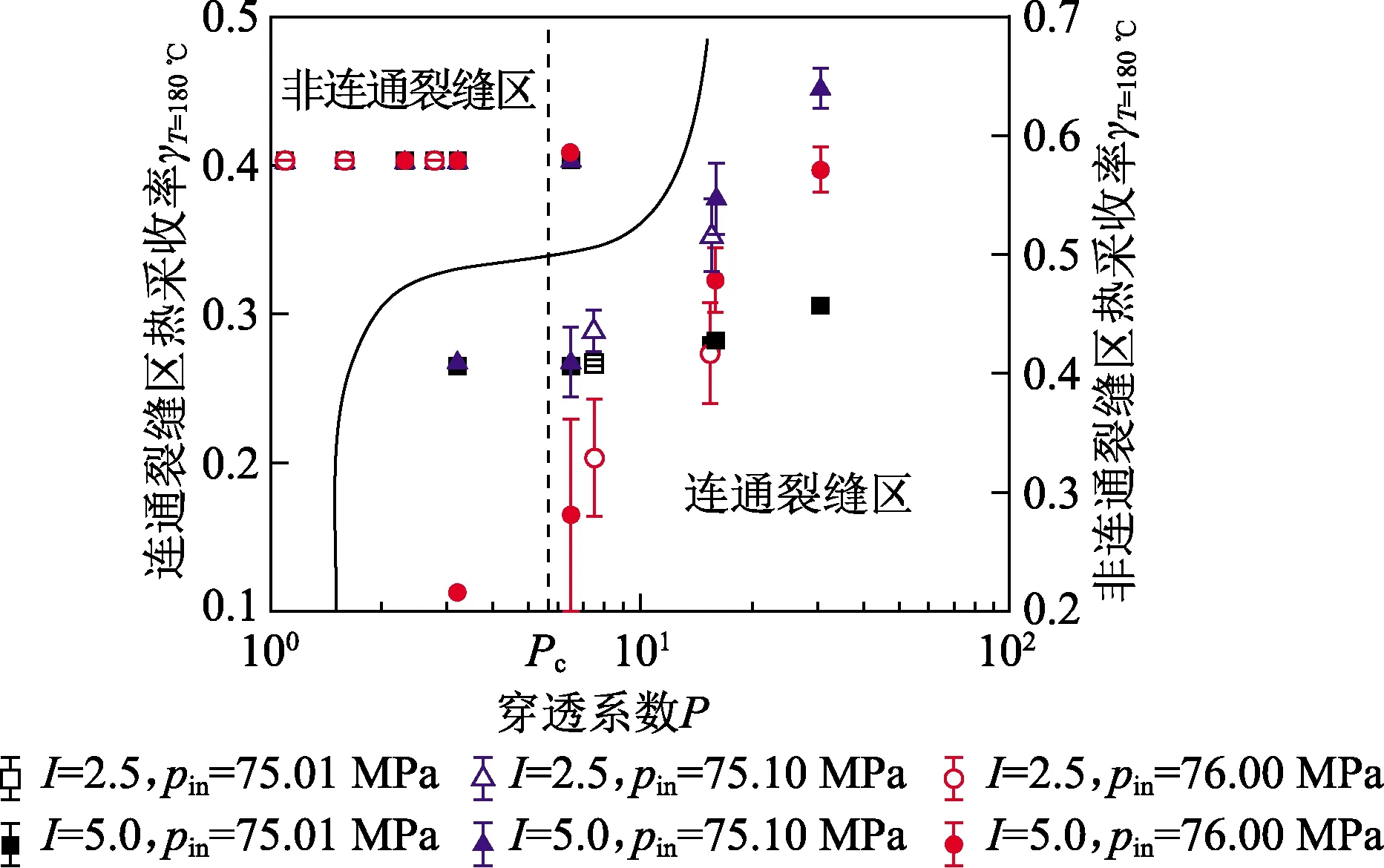
图8 不同注入压力下不同裂缝网络在出口温度 为180 ℃时的热采收率Fig.8 Heat recovery at T=180 ℃ with different fracture networks under different injection pressures
因此在以CO2为换热工质的增强型地热系统中,开发前压裂施工应尽可能使储层形成高裂缝密度和连通性的裂缝网络,增大换热面积。同时,在开发方案制定时采取适当的生产压差,使其满足生产要求的同时,避免冷水过早地突破。
5 结 论
(1)深部高温岩石裂缝系统渗透率对地热开发的效果起决定作用,干热岩内部有效的贯通裂缝是CO2流动及取热的关键,岩石整体渗透率在开发过程中最高可提高10~20倍。岩石内孤立的裂缝虽然对等效渗透率变化有所扰动,但是对于地热开发的关键时期(T> 180 ℃)影响很小。
(2)生产压差提高可加快热抽汲速率,同时穿透系数P越大,系统的换热面积也越大,出口温度突破曲线以及热采收率变化曲线的长尾效应越小。
(3)不同裂缝储层的开发效果对生产压差有不同的响应。裂缝强度和连通性较高的岩石能比较充分地利用岩石热量,可以在高流量下仍保持较高的热波及;对于裂缝强度和连通性较低的岩石,升高压差会导致注入冷水快速突破,极大缩减开发寿命。
