单桩基础灌浆连接段受力机理分析

房 奇，陈 涛，张持海，陈 珂，元国凯

(1. 同济大学 建筑工程系，上海 200092; 2. 工程结构性能演化与控制教育部重点实验室，上海 200092; 3. 中国能源建设集团 广东省电力设计研究院有限公司，广东 广州 510663)

全球海上风电场建设中，灌浆连接是应用最为成熟的基础连接方式，起到了传递风电机组荷载至地基基础中的关键作用[1]。近年来，风力发电发展迅速，风力发电机的功率越来越大，对灌浆连接段的受力性能提出了更高的要求[2-3]。在风荷载、浪荷载和重力荷载等同时作用下，灌浆连接段的受力情况较为复杂，对单桩结构灌浆连接段来说，主要承受轴力和弯矩同时存在的压-弯作用[4-5]。因此，准确评估灌浆连接段在压-弯作用下的受力机理和受力性能，对保证其正常工作及指导设计具有重要意义[6]。

对于轴力或者弯矩单独作用下灌浆连接段的受力机理，国内外学者进行了诸多研究。在轴向加载方面，Lamport等[7]和Krahl等[8]针对有剪力键灌浆连接段，提出了两种相似的斜压短柱承载力计算模型；Jeong-Hwa[9]对采用高强灌浆料(>120 MPa)的灌浆连接段展开研究，发现灌浆层斜裂缝的角度在25°～65°之间，并提出了灌浆连接段在轴向荷载作用下的初始强度和极限强度的概念。在弯矩加载方面，Andersen和Petersen[10]对风电场所采用的灌浆连接段进行了抗弯加载试验，发现剪力键提高了灌浆连接段的抗弯刚度且有助于其传递弯矩；Wilke[11]采用四点弯曲的加载方式对灌浆连接段试件进行弯曲受力试验，发现与传递轴向力相似，灌浆连接段也通过内外管之间的斜压短柱传递弯矩。

为研究轴力对灌浆连接段受弯性能的影响，Chen等[12]设计了静力压-弯承载力试验，发现灌浆连接段破坏模式为底部外钢管鼓屈，并发现在轴压比增大时，压-弯试件最大水平承载力减小，延性也会减小。基于国内外学者对灌浆连接段承载机理的研究，以静力压-弯承载力试验为依据，通过数值分析的方法，对在压-弯情况下轴压比对灌浆连接段性能的影响展开分析：主要从荷载-位移曲线、接触压力和应力状态三方面对灌浆连接段压-弯作用下的承载力变化进行了分析；从抗弯承载力组分构成和剪力键不均匀性受力两方面对灌浆连接段压-弯作用下的承载力组分构成变化进行了分析。

1 数值模型的建立与验证

1.1 数值模型参数设计

共设计6个灌浆连接段试件，试件编号以及所施加的轴向荷载如表1所示。

表1 灌浆连接段试件编号与轴压比Tab. 1 The number and the axial load ratio of the grouted connections

GC-ZW-0～ GC-ZW-5试件的几何尺寸均保持一致，其剪力键布置符合DNV规范的要求，布置在灌浆连接段中部二分之一的区域，如图1所示。表2给出了灌浆连接段几何尺寸的详细数值。

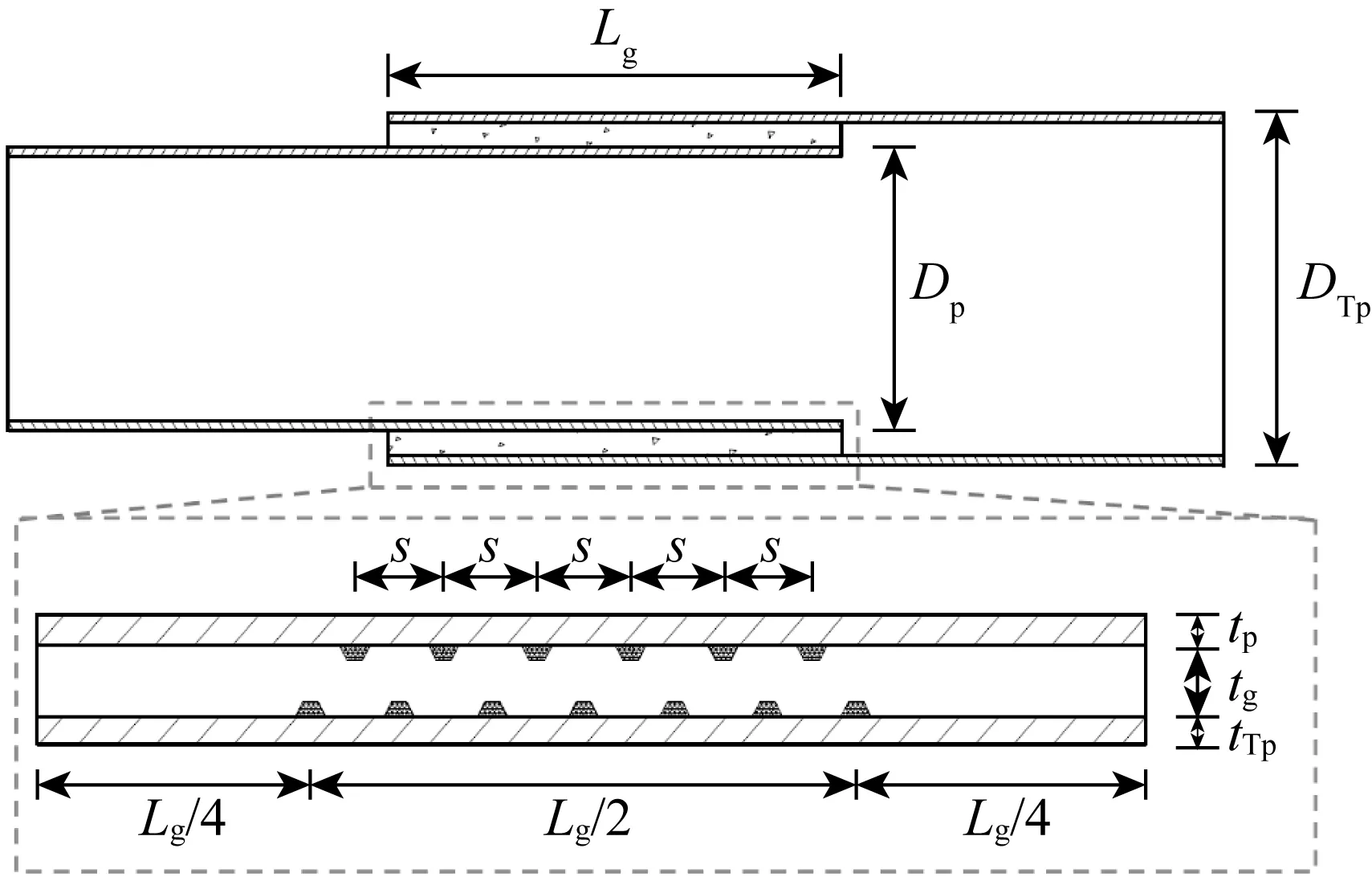
图1 灌浆连接段试件尺寸示意Fig. 1 Dimensions of the specimens of the grouted connections

表2 数值分析模型几何尺寸Tab. 2 The geometry of the numerical model

1.2 数值模型建立

灌浆连接段数值模型与网格划分如图2所示。通过建立对称面约束的方式将模型简化为半模型，提高计算效率。本构关系方面，钢材采用两折线模型，灌浆料采用混凝土塑性损伤(CDP)模型[13]。

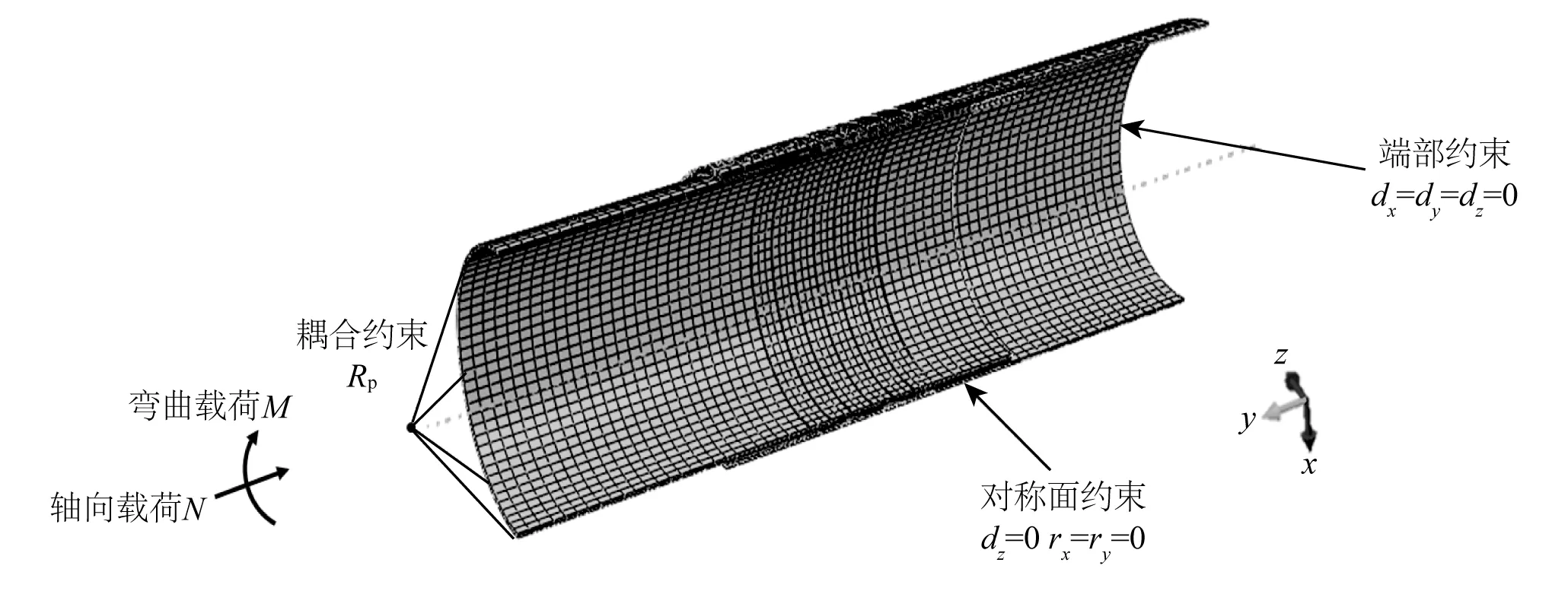
图2 灌浆连接段数值模型与网格划分Fig. 2 The numerical model and mesh of the grouted connections

建模方式采用分离体式建模，通过接触关系来定义钢管与灌浆料之间的相互作用，法向上定义为硬接触[14]，切向上则采用库伦摩擦的方式进行定义[15]。在外钢管端部施加固定约束，并在内钢管端部定义参考点Rp，在参考点与内钢管顶面之间定义耦合约束，从而获得所需数据。

数值模型的加载方式为先施加轴力到设定值，再施加弯矩。轴向荷载的施加采用均布荷载的方式，且为力加载。弯矩的施加方式为位移加载，通过对灌浆连接单耦合参考点Rp施加位移角来进行加载。数值模型的求解采用Newton-Raphson法进行，同时考虑几何大变形，通过设置增量大小和最大增量数控制计算量和计算精度。

1.3 数值模型的验证

为确保数值计算的可靠性，选取陈涛等[16]进行的压-弯缩尺试验中GC-1 试件和GC-2试件进行数值建模，并对比其破坏模式、荷载-位移曲线和极限承载力。GC-1试件和GC-2试件的基本尺寸设计如表3所示。

表3 压-弯试验试件尺寸

破坏情况方面，试验试件和数值模型的对比如图3所示，破坏方式均呈现为外管底部鼓曲破坏；荷载位移曲线方面，如图4所示，曲线吻合好、重合度高；极限承载力方面，GC-1试件与数值模拟误差为5%(试验结果为879.9 kN，数值模拟结果为835.2 kN)，GC-2试件与数值模拟误差为1%(试验结果为791.7 kN，数值模拟结果为797.8 kN)。因此，采用数值模拟方法可行。

图3 破坏模式对比Fig. 3 Comparison of failure modes

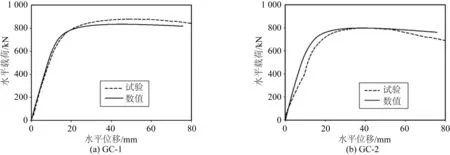
图4 荷载位移曲线对比Fig. 4 Comparison of load displacement curves

2 轴压比对灌浆连接段抗弯承载力的影响

灌浆连接段抗弯承载力的衡量方式多种多样，选取三个不同的层次，即荷载-位移曲线、接触压力和应力状态，对轴压比的影响进行详细讨论。

2.1 灌浆连接段在压-弯荷载作用下的荷载-位移曲线分析

在不同的轴压比n下，灌浆连接段弯矩承载力M-θ曲线汇总结果如图5所示。灌浆连接段试件的荷载-位移曲线均出现了明显的线性段和塑形段，因此灌浆连接段的压-弯破坏为延性的破坏模式。

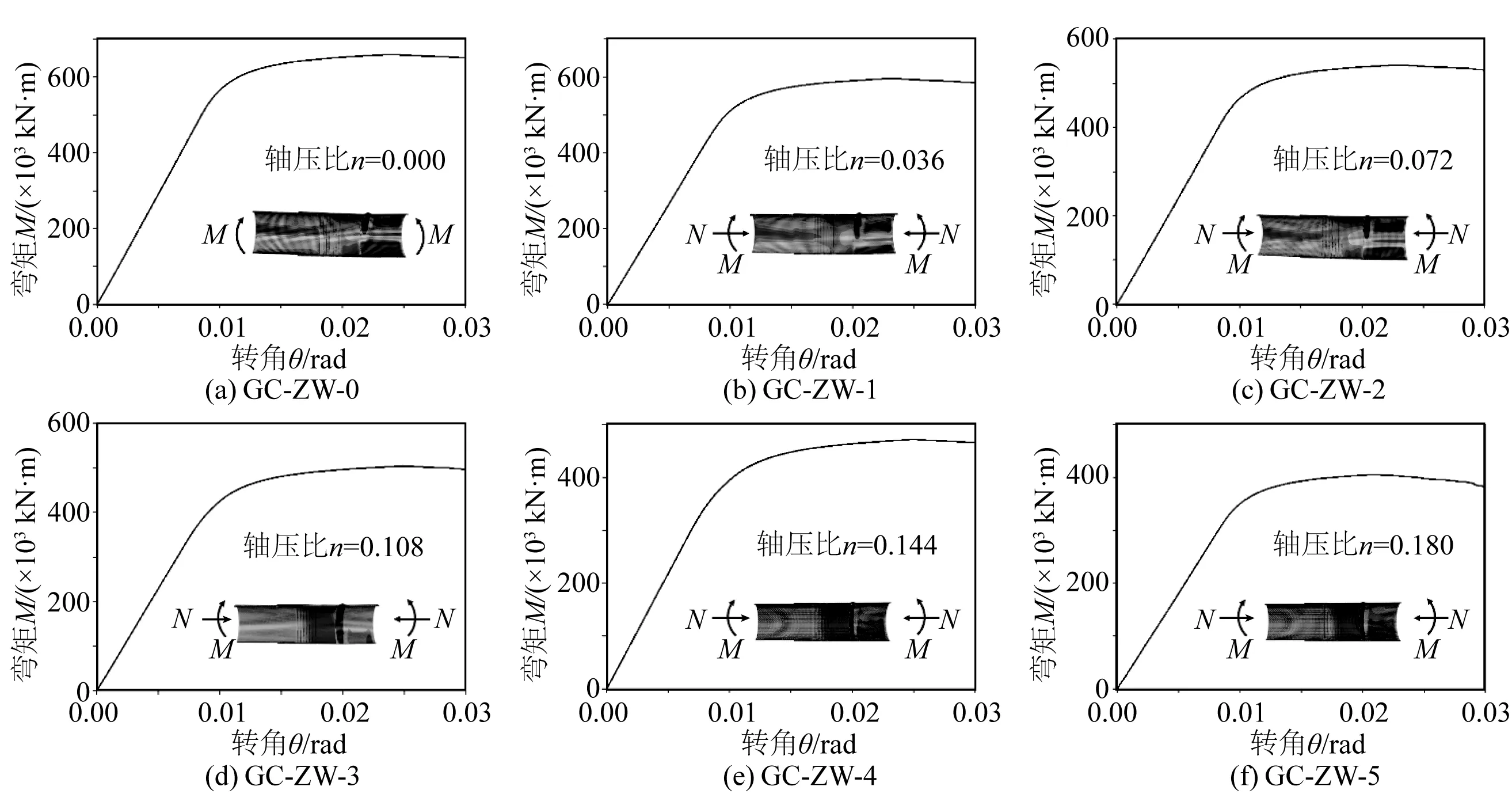
图5 灌浆连接段GC-ZW-0～ GC-ZW-5试件的M-θ关系曲线Fig. 5 M-θ curves from GC-ZW-0 to GC-ZWs-5

文中延性系数采用了Mustafa的位移延性系数[17]定义：如图6所示，灌浆连接段的屈服位移点定义为两切线(初始刚度切线与峰值荷载切线)的交点，对应的延性系数定义为极限荷载对应位移值θu与屈服荷载对应位移值θy之间的比值，即μθ=θu/θy。

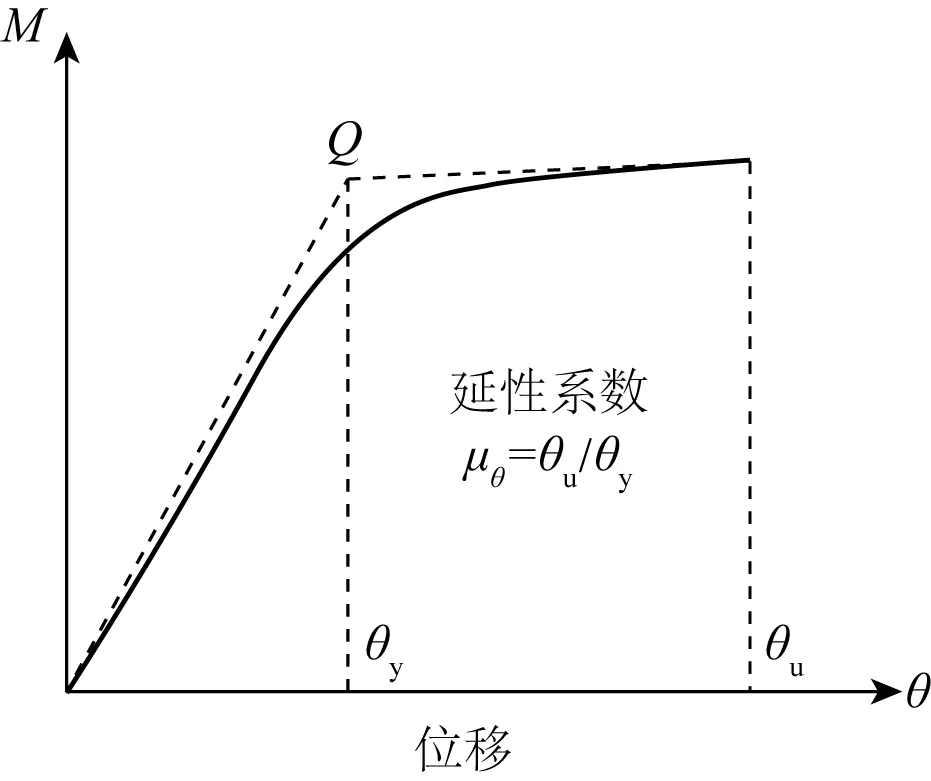
图6 位移延性系数的定义Fig. 6 Definition of ductility index

将灌浆连接段荷载-位移曲线的关键参数进行提取，比较轴压比对其极限抗弯承载力、曲线刚度以及延性系数的影响，如图7所示。从图中可以看出，轴压比对这三个关键参数的影响都是不利的。极限抗弯承载力方面，轴压比从0增大到0.180，承载力减小了约39%，可见轴压比对其影响显著；曲线刚度方面，轴压比增大，灌浆连接段的初始刚度和相对刚度都有不同程度的减小；延性系数方面，轴压比从0增大到0.180，延性系数减小了约23.6%。因此，在设计过程中，将轴压比作为抗弯承载力的一个重要考量因素，是必要的。

图7 荷载-位移曲线关键参数提取比较Fig. 7 Comparison of key parameters of load-displacement curve

2.2 灌浆连接段在压-弯荷载作用下的端部接触压力分析

2.2.1 DNV规范对于接触压力分布的规定

现行的DNV规范对于灌浆连接段在弯矩作用下的理论分析采用了Lotsberg的理论，其对接触压力的分布给出了若干理想化的假定，在纵向上，受拉侧与受压侧均呈现倒三角形分布；在环向上，灌浆连接段抗弯的受压侧(b点到d点)，接触压力是环向均匀分布的，数值为常数p；灌浆连接段抗弯的受拉侧(从d到a和从b到a)，接触压力为线性分布(从常数p递减到0)。DNV规范对于接触压力分布的示意如图8所示。

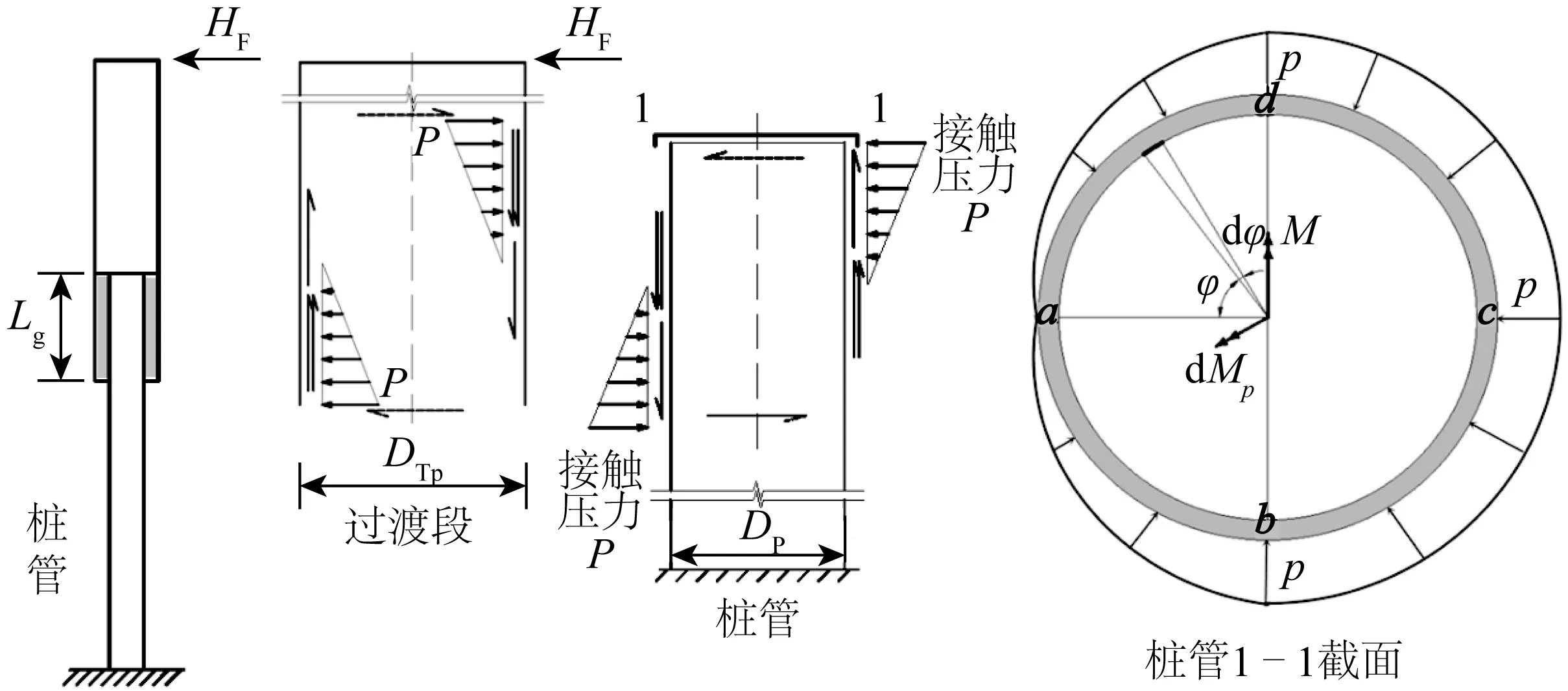
图8 灌浆连接段接触压力理论分布Fig. 8 Theoretical distribution of contact pressure of grouted connections

DNV规范规定，端部接触压力p的数值不可超过1.5 MPa，以此来验算灌浆连接段的极限受力状态。然而，其对于端部接触压力的分布给出了一个相对理想化的假定，这与实际情况可能存在差异。为此，提取了数值模型计算结果中的端部接触压力，并对其分布规律进行了简要分析。

2.2.2 数值模型中端部接触压力分布分析

如图9所示，灌浆连接段受拉侧定义为0°，受压侧定义为180°。沿着灌浆连接段灌浆体端部的内表面环向均匀等分，提取11个单元的接触压力。单元的接触压力是其接触表面对应4个点的接触压力的平均值。

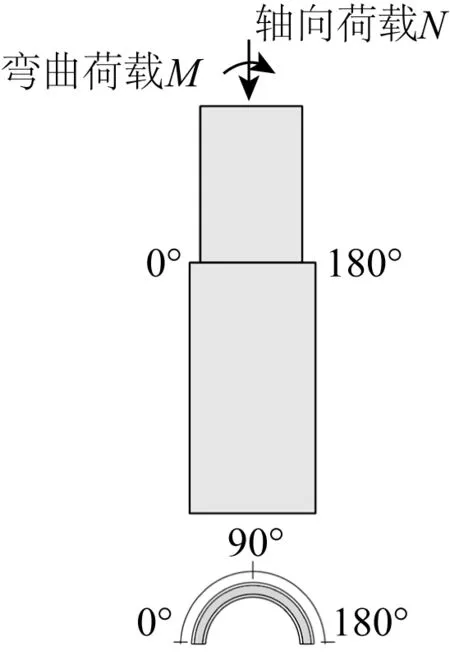
图9 灌浆连接段角度坐标系定义Fig. 9 Angle coordinate system definition of grouted connections

图10给出了轴压比n对灌浆连接段端部环向接触压力分布规律的影响，图中所示的接触压力为灌浆连接段在达到极限抗弯承载力Mmax时的接触压力。其中横坐标为环向角度，单位为(°)，纵坐标为接触压力，单位为MPa。观察曲线分布规律可以发现，灌浆连接段在不同轴压比下，环向接触压力的分布规律基本是一致的，只是在数值上存在差异。0°～40°的位置灌浆连接段的环向接触压力均为零，从环向40°的位置到180°的位置，接触压力的数值在不断提升，在180°位置处灌浆连接段的接触压力达到峰值。

随着轴压比n的增加，相同环向角度位置处的接触压力不断降低，在整体曲线上宏观表现为高轴压比的接触应力分布曲线位于低轴压比的接触应力分布曲线的下方。造成这种结果的原因在于，轴力的存在使得内外钢管剪力键之间的相互作用加强。在这种情况下，内钢管的弯矩传递给外钢管时更多地依靠内外交错剪力键的机械咬合作用，而不是接触压力，宏观上就体现为端部的接触应力数值在不断降低。

图11给出了轴压比n对灌浆连接段端部环向接触压力峰值的影响，即轴压比n对环向180°位置处的峰值接触压力的影响。图中横坐标为轴压比n，纵坐标为接触压力，单位为MPa。图中的黑色柱体代表模型中轴力加载完成，尚未加载弯矩时的峰值接触应力，灰色柱体代表灌浆连接段达到极限抗弯承载力时的峰值接触应力。可以发现，数值模型中，当轴力加载完成尚未施加弯矩时，随着轴压比n的增加，峰值接触压力在不断增加，从0 MPa增加到1.49 MPa。而当灌浆连接段达到极限抗弯承载力时，随着轴压比n的增加，环向180°位置处的峰值接触压力是在不断减小的。轴压比n从0增加到0.180时，灌浆连接段的端部峰值接触应力从3.45 MPa 减少到了2.11 MPa。

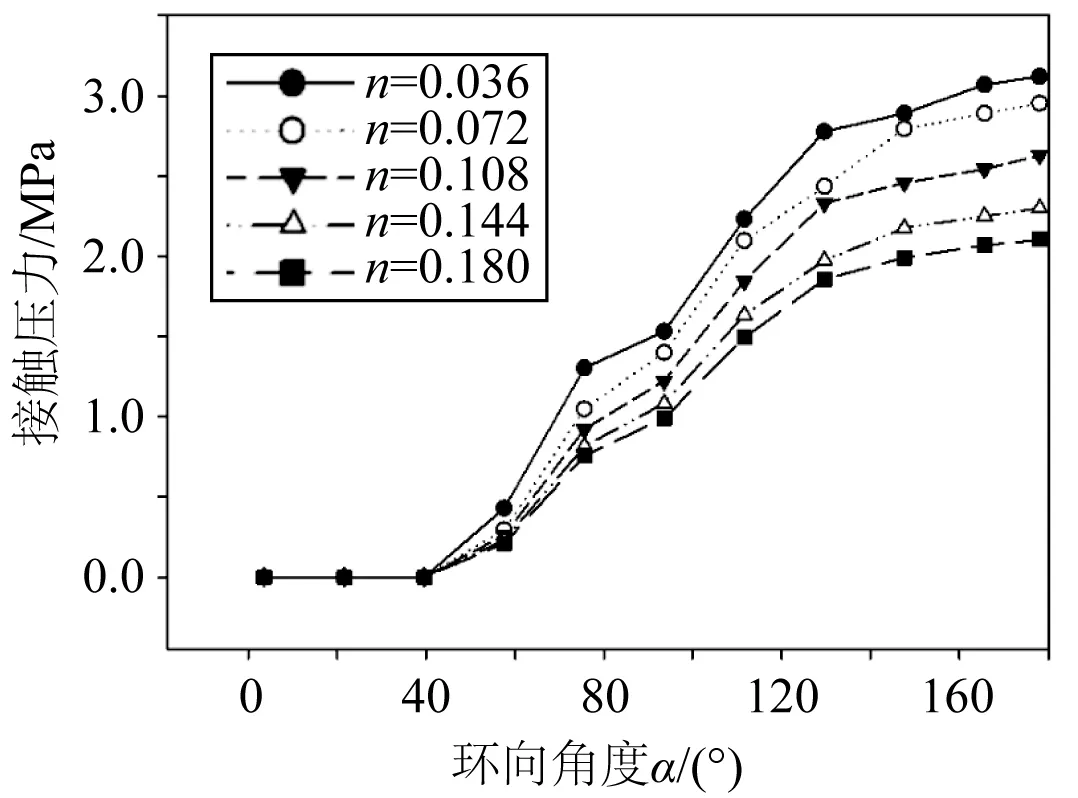
图10 轴压比对灌浆连接段端部环向接触压力分布的影响Fig. 10 Effect of axial load ratio on the circumferential contact pressure distribution

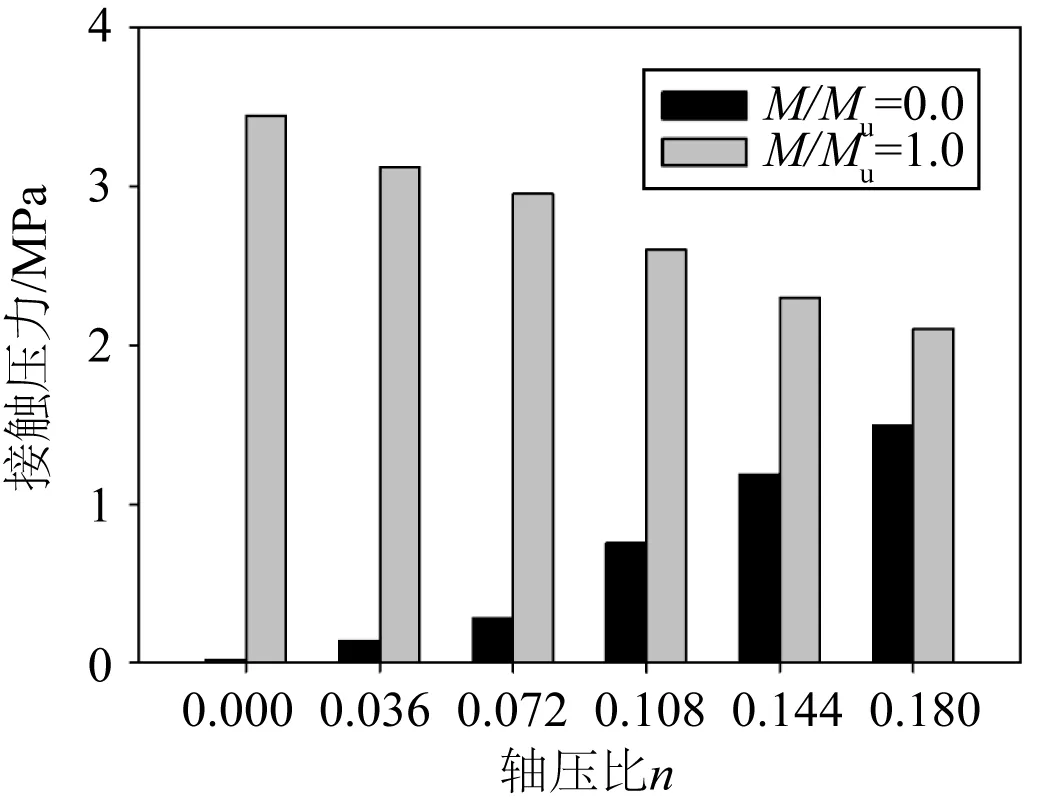
图11 轴压比对灌浆连接段端部环向接触压力峰值的影响Fig. 11 Effect of axial load ratio on peak contact pressure

数值的计算结果表明，DNV规范中强调灌浆连接段端部接触压力不能超过1.5 MPa，这是相对比较保守的。另一方面，轴压比n会对灌浆连接段端部接触压力的分布存在一定的影响。当前的设计仅从抗弯承载力的角度控制灌浆连接段端部的接触压力，而没有考虑轴力作用的影响，该设计方法设计的结构可能偏不安全，设计方法有待进一步改进。

2.3 灌浆连接段在压-弯荷载作用下的应力状态分析

以GC-ZW-1 试件为例，对灌浆连接段在压-弯荷载下的应力分布规律进行分析说明。图12和图13分别给出了灌浆连接段内钢管及外钢管的Mises应力分布规律。在压-弯作用下的灌浆连接段钢管应力分布较为不均匀，在钢管的受压侧以及受拉侧部分，应力水平较高。由于剪力键的存在，内钢管的应力云图从上至下呈现出锯齿形的分布规律，且整体的应力水平不断降低，这表明弯矩和轴力通过灌浆层与钢管的接触作用有效的从内钢管传递到了外钢管。

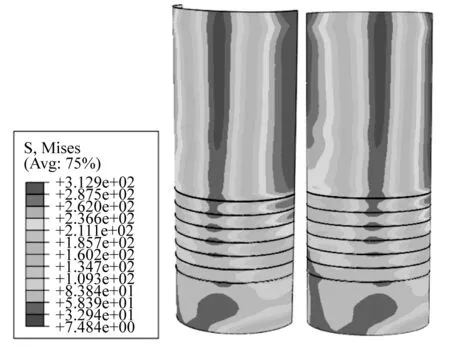
图12 灌浆连接段内钢管Mises应力分布Fig. 12 Mises stress distribution of inner steel tubes

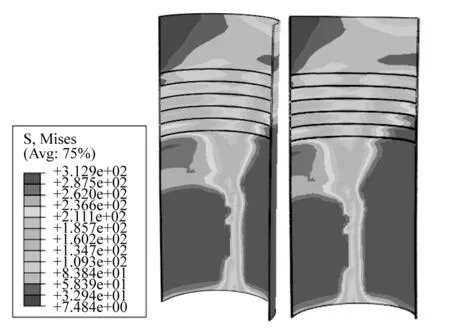
图13 灌浆连接段外钢管Mises 应力分布Fig. 13 Mises stress distribution of outer steel tubes

图14给出了灌浆连接段的灌浆层在压-弯作用下的Tresca应力分布状况。图中显示的结果表明，灌浆层在内外交错的剪力键之间形成了一个个斜压短柱，并且可以看出，各斜压短柱的受力情况并不均匀。在灌浆连接段的受压侧(180°位置)，第一个斜压短柱受力较大，随后从左至右斜压短柱的受力逐渐减小。而受拉侧情况则是相反的，第一个斜压短柱受力较小，随后从左至右斜压短柱的受力逐渐增加。

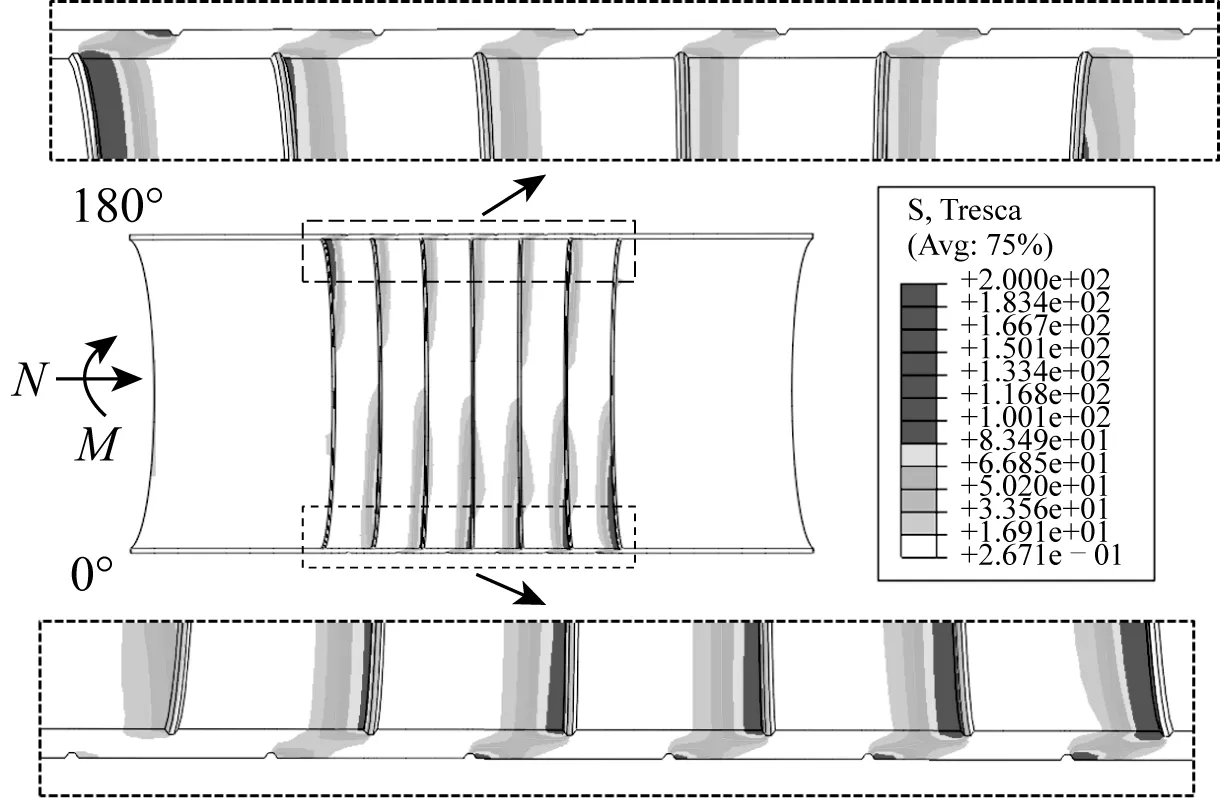
图14 灌浆层Tresca应力分布Fig. 14 Tresca distribution of grout

3 轴压比对灌浆连接段抗弯承载力组分构成的影响

3.1 抗弯承载力组分数值积分方法

Lotsberg等[15, 18]认为灌浆连接段的抗弯承载力由4部分组成：灌浆连接段两端部钢管与浆体间的接触压力p形成的抗弯承载力Mp，钢管与浆体间水平方向的摩擦力Fμh形成的抗弯承载力Mμh，钢管与浆体间竖直方向摩擦力Fμv形成的抗弯承载力Mμv，剪力键贡献的抗弯承载力Mshear-keys。抗弯承载力M的表达式为[15, 18]：

M=Mp+Mμh+Mμv+Mshear-keys

(1)

通过数值分析计算的方法，可以得到灌浆料与钢管之间接触力分布的数值解。对于灌浆料与钢管的相互作用，相较于人为理想化的接触力分布假定，数值模型中给出的数值解提供了另一种分析的角度，可以为实际工程设计提供参考。通过Python语言进行自动提取并且进行后处理，使得提取结果更为精确。设灌浆连接段受弯时绕灌浆连接段中心点旋转。以灌浆连接段中心点为原点作矩，得到抗弯承载力组分的表达式如下所示，模型示意如图15所示。

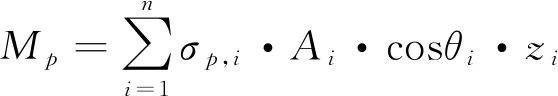
(2)

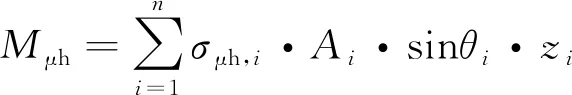
(3)

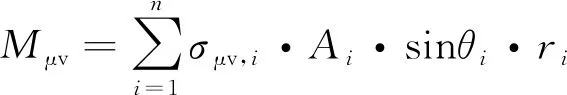
(4)

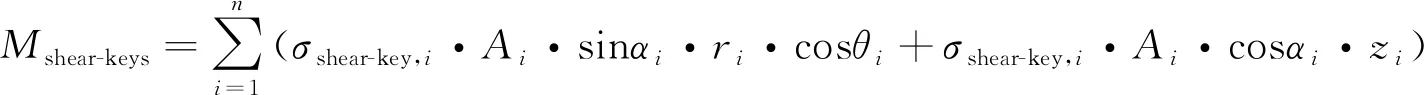
(5)

其中，Mp为由接触压力贡献的抗弯承载力；Mμh为由水平摩擦力贡献的抗弯承载力；Mμv为由竖向摩擦力贡献的抗弯承载力；Mshear-keys为由竖向摩擦力贡献的抗弯承载力；σp, i为第i个接触单元上的接触压力；σμh, i为第i个接触单元上的水平摩擦力；σμv,i为第i个接触单元上的竖向摩擦力；σshear-keys, i为第i个剪力键接触单元上的接触压力；Ai为第i个接触单元的面积；ri,θi,zi为柱坐标系中，接触单元中心点的坐标；αi为接触单元法线方向与水平面的夹角。

3.2 抗弯承载力组分构成研究

以GC-ZW-1试件为例，根据图16，其中灌浆连接段端部钢管与浆体间的接触压力p形成的抗弯承载力为Mp，钢管与浆体间水平方向的摩擦力Fμh形成的抗弯承载力为Mμh，钢管与浆体间竖直方向摩擦力Fμv形成的抗弯承载力为Mμv，剪力键贡献的抗弯承载力为Mshear-keys，各部分抗弯承载力以Mi表示，总抗弯承载力以Mtot表示，施加弯矩以M表示，极限弯矩以Mu表示。在受力全过程中，灌浆连接段的抗弯承载力组分以接触压力所提供的组分以及剪力键所提供的组分为主，两者之和占比达75%左右，而摩擦力所提供的抗弯承载力组分占比较小。随着压-弯荷载作用水平的不断增大，灌浆连接段中接触压力所提供的抗弯承载力组分占比不断降低，占比从47.7%降低到40.8%。同时，摩擦力组分占比提升较为明显，水平摩擦力组分从3.8%提升到7.8%，竖向摩擦力组分从7.5%提升到15.6%，剪力键所提供的组分占比也略有提升。分析可知，随着压-弯荷载水平的不断增大，灌浆层和钢管之间的接触越来越紧密，摩擦力和剪力键对抗弯的贡献越来越大，因此出现此趋势。另外，接触压力和剪力键在抗弯承载力中起着重要作用，应引起重视。

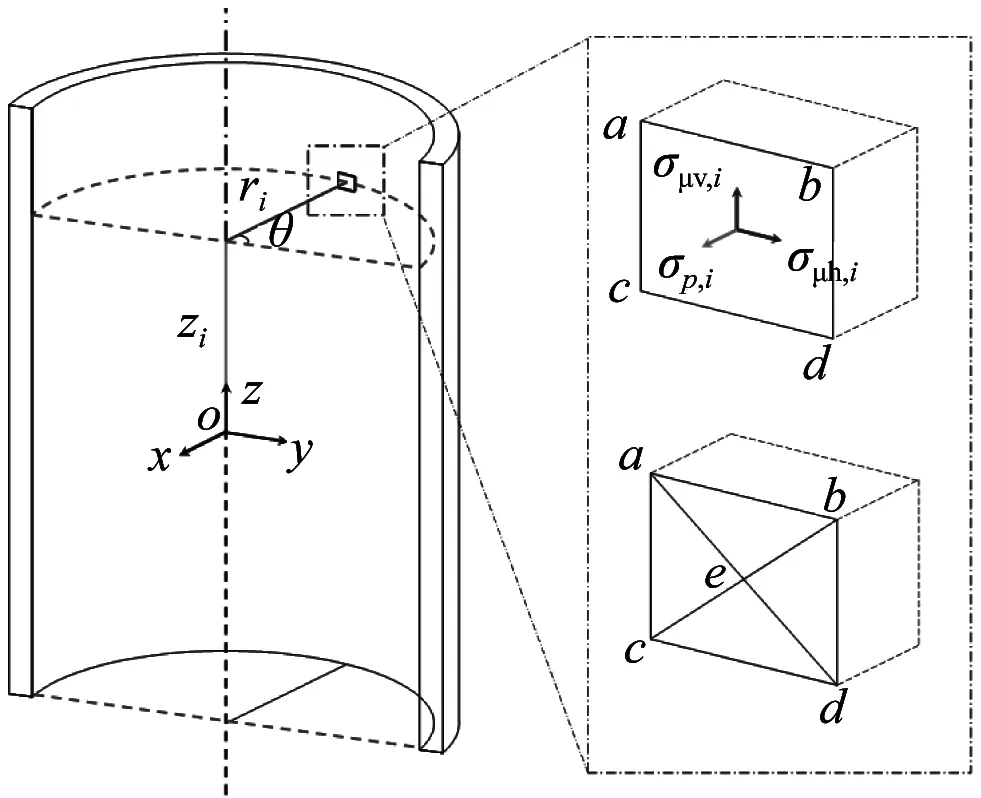
图15 灌浆连接段单元体分析模型Fig. 15 Unit analysis model of grouted connections

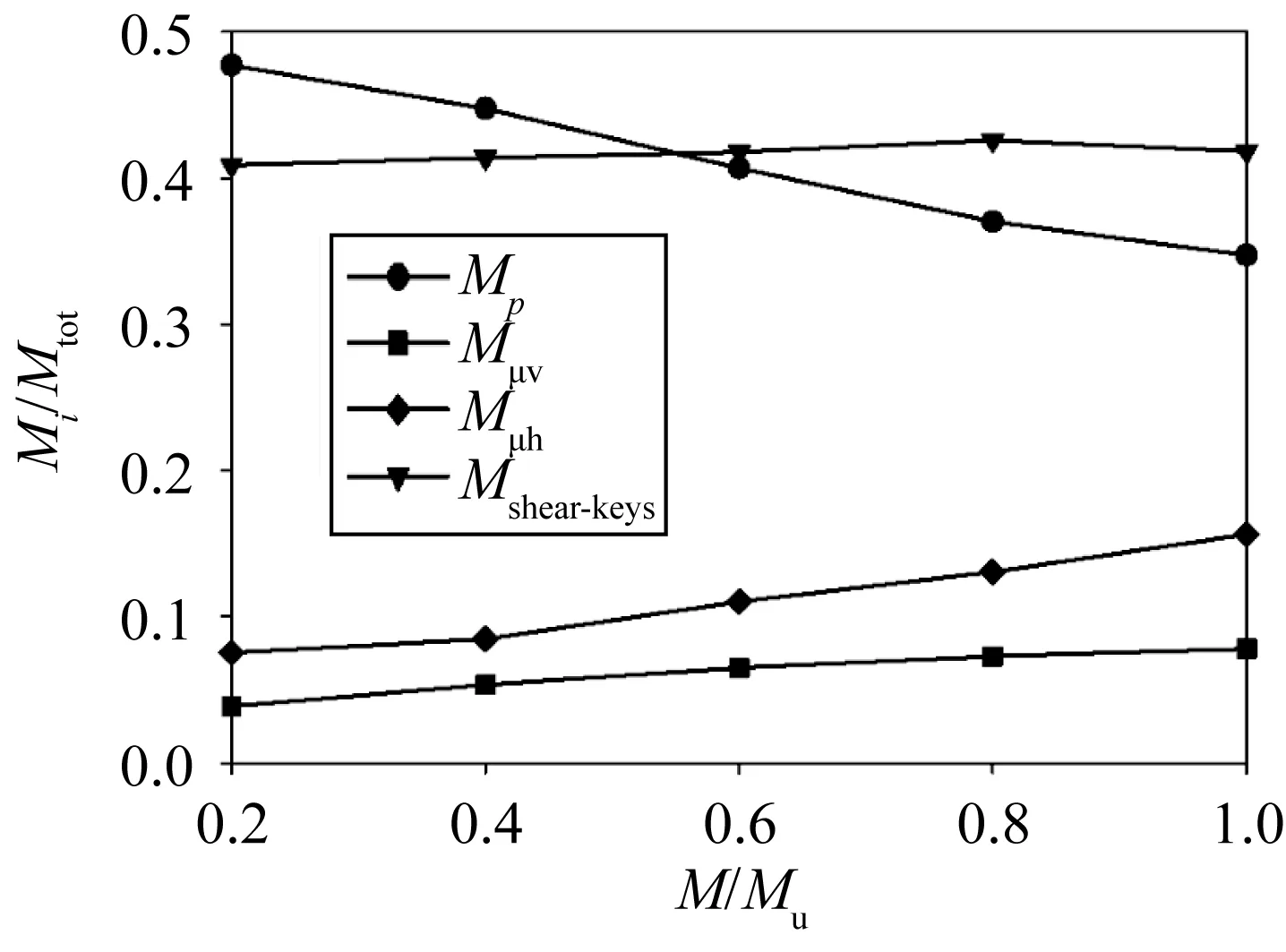
图16 GC-ZW-1试件抗弯承载力组分全过程变化规律Fig. 16 Flexural capacity component of GC-ZW-1 specimen

轴压比对抗弯承载力组分构成的影响情况如图17所示。随着轴压比n的不断增大，接触压力提供的抗弯承载力不断减小。当轴压比从0增加到0.180时，接触压力组分的占比从37.1%减少到30.4%，与此同时，剪力键所提供的抗弯承载力组分却随着轴压比的增加而不断提高，占比从40.1%增加到了47.1%。数值积分计算的结果显示，轴压比n对摩擦力所提供的抗弯承载力组分影响较小。其中水平摩擦力提供的抗弯承载力组分占比的值稳定在7%左右，而竖向摩擦力所提供的抗弯承载力组分占比的值为15%左右。分析可知，随着轴压比的增大，轴向压力使得剪力键之间产生更强的相互作用，从而能够贡献更多的抗弯承载力，接触压力提供部分由此减少，因此，在灌浆连接段中，随着轴压比的增大，剪力键的作用愈发凸显。

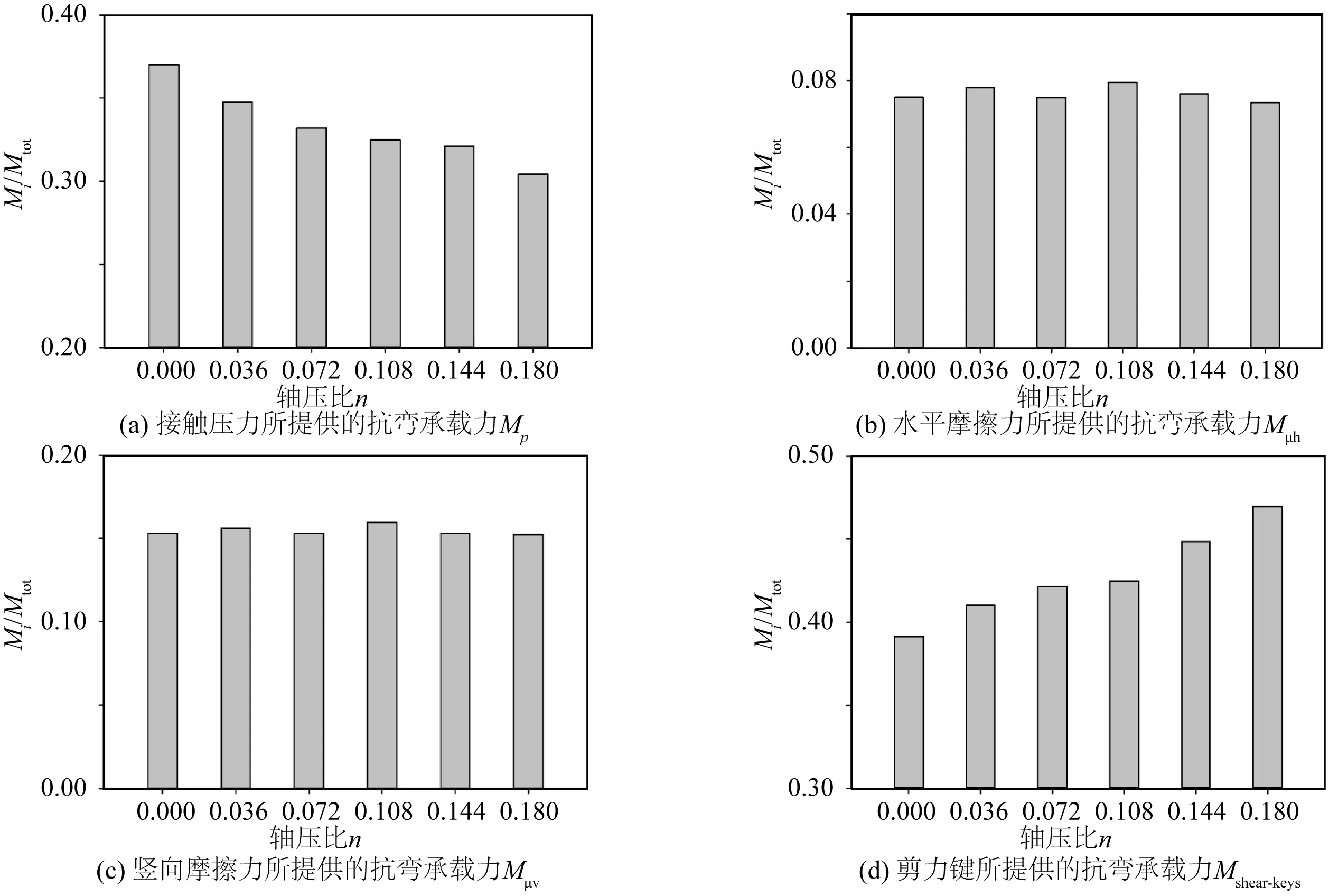
图17 轴压比对抗弯承载力组分构成的影响Fig. 17 Effect of axial load ratio on the composition of the flexural capacity

4 结 语

对灌浆连接段在压-弯作用下的受力性能进行了讨论分析，重点探讨了不同轴压比下灌浆连接段抗弯承载力性能的差异，提出了灌浆连接段抗弯承载力组分数值积分分析方法，并得到如下结论：

1) 轴压比n对于灌浆连接段的抗弯承载力具有不利影响。随着轴压比n的增加，灌浆连接段抗弯承载力不断下降，对应的荷载-位移曲线刚度降低，并且延性逐渐变差。轴压比从0 增加到0.180，灌浆连接段抗弯承载力降低了约40%。

2) 灌浆连接段端部环向的接触压力分布数值解与DNV规范的理论假定分布形式存在一定的差异。在压-弯作用下，采用数值分析方式，对灌浆连接段进行数值分析时，发现灌浆连接段端部环向0°～40°的位置接触压力均为零，在180°位置接触压力达到峰值。随着轴压比n的增加，相同环向角度位置处的接触压力不断降低。

3) 在压-弯作用下，灌浆连接段灌浆层在内外交错的剪力键之间形成了斜压短柱进行传力，应力云图显示，各斜压短柱受力情况并不均匀。

4) 数值积分计算结果显示，灌浆连接段的抗弯承载力组分以接触压力所提供的组分Mp以及剪力键所提供的组分Mshear-keys为主，两者之和占比达75%左右。轴压比n的存在对抗弯承载力组分构成占比存在一定的影响。随着轴压比n的不断增大，接触压力提供的抗弯承载力Mp不断减小，剪力键所提供的抗弯承载力组分Mshear-keys却随着轴压比n的增加而不断提高。