天然气水合物开采区内海床不均匀沉降对管道力学性能的影响

谢 鹏，常江涛，肖卓临

(1. 中山大学 海洋工程与技术学院，广东 珠海 519082; 2. 南方海洋科学与工程广东省实验室(珠海)，广东 珠海 519082)

天然气水合物广泛存在于海底的沉积物中，分布范围广、资源量巨大、能量密度高，是一种高效的清洁能源。现行的水合物开采方法主要有加热法、降压法、注入外加剂法等[1]，其基本原理是通过改变水合物所处环境的温度和压力，打破水合物稳定存在的平衡条件，使其分解为天然气。国际上已经有少数国家开展了水合物试采，其中产量最高的是我国于2017年5月10日实施的在我国南海神狐海域水合物试采，累计试采稳定产气60 d，总计产气量为30.9×104m3，其中最高日产为3.5×104m3/d，完成了验证我国水合物开采关键技术的目标[2]。根据国家规划，预计2030年实现天然气水合物的产业化开采，建成产能达到10×108m3的大型气田。根据最高产量3.5×104m3/d的产量进行保守估计，建造一个10×108m3的大型气田，日均产量约为273×104m3。为实现这一目标，预计需要在气田内布设78口同等流量的产气井进行同时开采和联合集输。因此，在大规模开发的天然气水合物开采区，必须要使用大量海底管道和管汇将各井口串联，并进行天然气集输。

天然气水合物的开采会诱发海床发生不均匀沉降，沉降会改变海底管道的受力状态，甚至导致管道发生大变形，造成管道发生屈曲、断裂、悬跨等失效[3-4]。大量研究表明，当天然气水合物在储层内分解后，水合物沉积层的结构会发生很大程度的扰动，其强度和力学特性也会发生改变，当水合物的开采量达到某一程度时，则会诱发海床发生不均匀沉降、海底滑坡、土层失稳等地质灾害[5]，历史上著名的挪威Storegga第二次海底滑坡，美国东海岸Carolina岸外的Cape Fear滑坡，西地中海的Balearic巨型浊流层和西非大陆架的海底滑坡体等事故都是由水合物分解造成的[6-7]。万义钊等[8]基于“热-流-固-化”四场耦合的水合物开采分析模型，研究了水合物开采早期的海床沉降规律和影响参数。研究发现，在开采第30天时，开采井位置处的最大沉降量为0.032 m，海底面沉降范围的半径约为166 m。开采第60天时开采井位置的最大沉降量为0.035 m，海底面沉降范围的半径约为232 m。金光荣等[9]通过建立南海神狐海域水合物降压开采模型，研究了更长时间开采范围内的海床沉降规律，获得了海床沉降量与开采时间的关系曲线，并针对开采井500 m范围内的海床沉降情况进行了详细分析。结果显示，开采第2年时，在开采井附近位置海床沉降量达到2.6 m，且随着开采时间和开采量的增加，海床沉降量增大。

然而，现有的研究主要针对天然气水合物开采过程中水合物的分解过程进行研究，并预测水合物开采过程引起的海床沉降规律，并未考虑布设在开采区范围内的海底管道等工程设施，也未研究水合物开采引起的海底管道受力状态和失效模式。为解决这一问题，基于有限元分析方法，建立天然气水合物开采区内“海床-管道”耦合作用模型，以“生死单元”模拟了天然气水合物开采过程中海床沉降过程，获得了海床变形形态及其对管道应力、应变、弯矩、悬跨等力学行为的影响。研究结果可以为建立天然气水合物开采区内海底管道的设计方法提供依据，为未来天然气水合物的大规模产业化开采做技术储备。

1 “管-土”相互作用的有限元分析

水合物开采过程中，位于井口附近的水合物先分解，这将会扰动开采井口附近区域的沉积层结构，改变沉积层的强度和力学特性，诱发海床发生不均匀沉降，而沉降最严重的区域就是开采井口，海床的沉降量以开采井口为中心向外辐射递减。研究位于水合物开采区内场(in-field)的海底管道，该管道需要与开采井口进行连接，在大规模的水合物开发过程中预计需要在气田内布设78口同等流量的开采井进行同时开采和联合集输，必须要使用大量的海底管道和管汇将各井口串联起来，因此必然导致海底管道经过井口附近。当管道从开采井口附近穿过时，由于海床的沉降，管道在自身重力下也会发生竖向位移，位移最大处位于开采井处，由于管道发生变形，管道的应力、应变、弯矩等力学特性也会发生相应的变化。因此，有限元模型的建立以海底管道跨越单井口为研究对象，模拟在进行单井口水合物开采时引起的海床沉降规律，及其对附近管道力学性能的影响。

1.1 海底管道模型

基于ABAQUS有限元软件进行数值模拟，管道模型全长600 m，管道半径0.31 m, 厚度0.02 m，如图1所示。管道模型采用X65钢，主要材料参数如表1所示。ABAQUS中适用于接触问题的单元须为减缩积分单元[10]，因此管道采用减缩积分的4节点曲面壳单元(S4R)，该单元是一种通用的壳单元类型，具有很好的适应性，既可以用于厚壳问题的模拟，也可以用于薄壳问题的模拟。减缩积分是相对于完全积分来说的，减缩积分单元比完全积分单元在每个方向上少使用一个积分点，在模型受弯曲时可以消除计算中的剪切锁闭问题且对计算结果的精度影响不大。

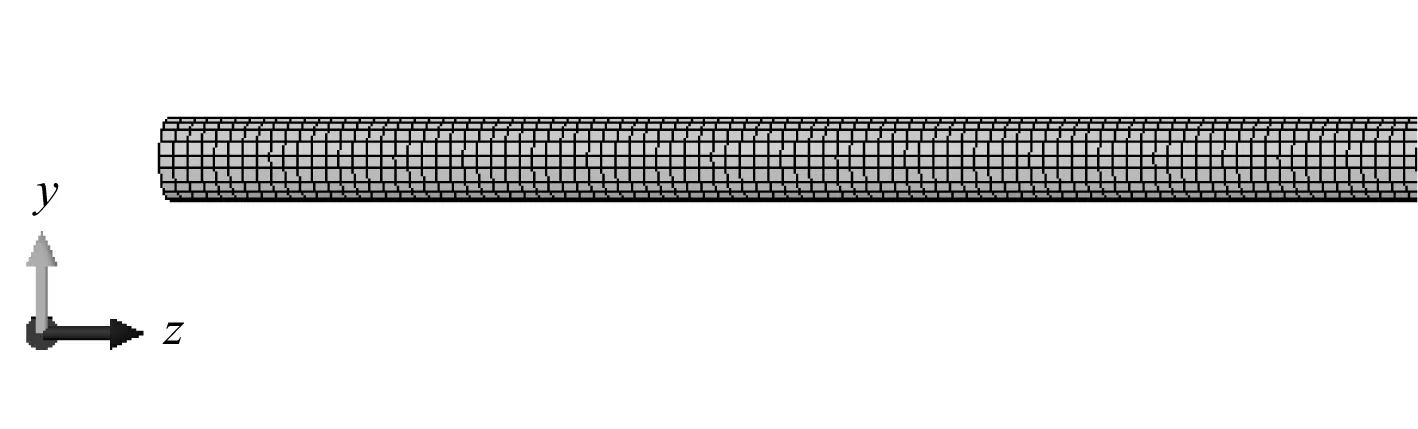
图1 管道模型Fig. 1 Pipeline model

表1 X65 钢材主要参数Tab. 1 Main parameters of X65

采用Romberg-Osgood方程建立管道材料的本构关系，其表达式为：

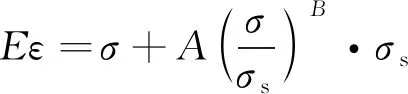
(1)

式中：ε是材料应变；σ是材料应力；E为弹性模量；σs是屈服强度；A和B是描述材料塑性应变的硬化参数，A=1.29，B=25.58 。

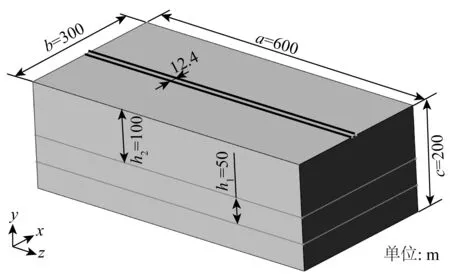
图2 海床模型Fig. 2 Seabed model

1.2 海床模型

将海床的不均匀沉降作为海底管道力学分析的边界条件，基于有限单元法的实体单元模拟水合物储层被开挖后海床的沉降变形过程，构造出“等效的”不均匀海床表面变形形态，不需要对水合物开采过程中的热量传递、固气转变等过程进行分析。分析时，海床选择减缩积分的8节点六面体单元(C3D8R)，该单元对模拟非常大的网格扭曲问题有很好的适应性，由于模型中海床会发生较大的变形，因此选用该单元进行网格划分。海床模型全长600 m，宽300 m，高200 m，其中天然气水合物层深度100 m，厚度50 m，海床上表面设置宽度为20倍管道直径的条带作为和管道接触的区域，如图2所示。海床模型材料简化为弹塑性材料，模型主要参数如表2所示。该模型的分析参数基于我国南海北部陆坡神狐海域天然气水合物的成藏规律确定，研究结果可以代表未来在该海域内海底管道沉降及受力分析的一般情况。

表2 海床主要参数Tab. 2 Main parameters of seabed

1.3 接触设置

管道外壁与海床上表面之间设置接触面，采用单纯的“主控-从属”接触算法。在计算过程中，为了获得较好的模拟结果，选择管道的外表面作为主接触面，海床的上表面取20倍管径宽度的条带区域作为从接触面。接触作用属性设置为法向“硬”接触，切向采用罚函数摩擦公式定义切向摩擦力。

2 基于“生死单元”模拟海床不均匀沉降过程

“生死单元”功能是为了克服有限元本身缺陷提出的一种分析方法，被广泛应用于矿产开采、隧道钻进、基坑开挖等岩土工程领域，用来模拟被开挖部分“消失”的情况[11-12]。该单元弥补了有限单元法常规单元的不足。由于有限元本身是基于连续介质力学的，所研究的物体需要是连续的，在这样的理论框架下，单元本身是不会消失的。然而在水合物开采过程中，由于水合物分解并经开采井运输后，势必在原区域产生短暂的环空，并造成海床沉降。因此，在进行数值分析时，需要模拟水合物储层单元消失或者完全失效的情况。为了模拟这种工况，采用ABAQUS“生死单元”功能进行研究。在移除单元之前，ABAQUS自动计算和储存待移除单元和余下单元交界面上的节点力，这些节点力在移除步中逐渐减少为零。在有限元分析过程中，通过分步移除水合物层一定范围内的单元，模拟水合物逐步开采的过程，在此基础上得到海床的不均匀沉降模型，如图3所示。具体分析过程可分为13个分析步。

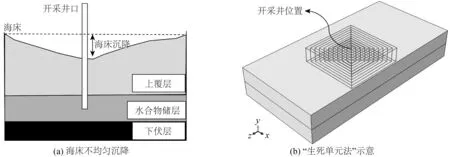
图3 海床的不均匀沉降模拟Fig. 3 Simulation of uneven subsidence of seabed

第1分析步：管道左端施加x、y、z三个方向的约束；右端施加x方向的约束，约束管道的横向位移。海床底面施加固定约束，海床左右两端施加x、y、z三个方向的约束。

第2分析步：为管道施加重力载荷，重力加速度取一较小值0.1 m/s2,使得管道与海床之间的接触作用平稳的建立起来。同时在管道的右端施加一水平张力T0来模拟管道内部的轴向拉力，其值为200 kN，此值主要根据工程经验得到。

第3分析步：为海床施加体力载荷，海床的重度为20 kN/m3,将管道受到的重力加速度改为10 m/s2。

第4分析步：从第4分析步(即第1步开采)开始模拟水合物的开采过程，开采井口设置在海床模型上表面的中心点处，开采位置设置在开采井口下100 m深的水合物层处，开采厚度50 m，开采范围20 m。开采过程通过ABAQUS中的单元生死功能实现，通过移除水合物层一定范围内的单元，来模拟逐步开采的过程。

第5～13分析步：重复第4分析步，开采范围以20 m为梯度逐步增大，共开采10步，最终开采范围为200 m。通过这种逐步开采的方式获得海床的沉降以及管道的力学响应。

3 天然气水合物开采区内海床沉降规律及验证

3.1 天然气水合物开采过程中海床不均匀沉降量

通过ABAQUS进行数值模拟，对水合物进行分步开采，得到开采过程中的每一步海床沉降量及形态分布结果，如图4、图5所示。提取第5、第7、第9和第10步开采的位移云图，开采影响范围分别为100 m、140 m、180 m和200 m，分别如图5所示。从图中可以明显的发现，随着开采范围的增大，海床的位移逐渐增大，第10步开采时，海床沉降量达到最大值3.543 m，位移云图显示的较大位移区域逐渐向开采井处收缩。

图4 海床位移云图Fig. 4 Displacement nephogram of seabed

图5 不同开采步下模型的位移云图Fig. 5 Displacement nephogram of models under different mining steps

3.2 海床沉降量规律的验证

以“生死单元”法模拟实体单元消失引起海床沉降变形，等效模拟真实开采过程中的海床沉降量和海床表面形态分布规律，结果如图6所示。x=0处为开采井，图6(a)为海床沉降量在模型长度方向上随开采井距离的变化曲线，图6(b)为海床沉降量在模型宽度方向上随开采井距离的变化曲线；曲线之间的变化趋势相同，海床沉降量随着与开采井距离的增大而减小。开采过程中开采井处的海床沉降量如表3所示。

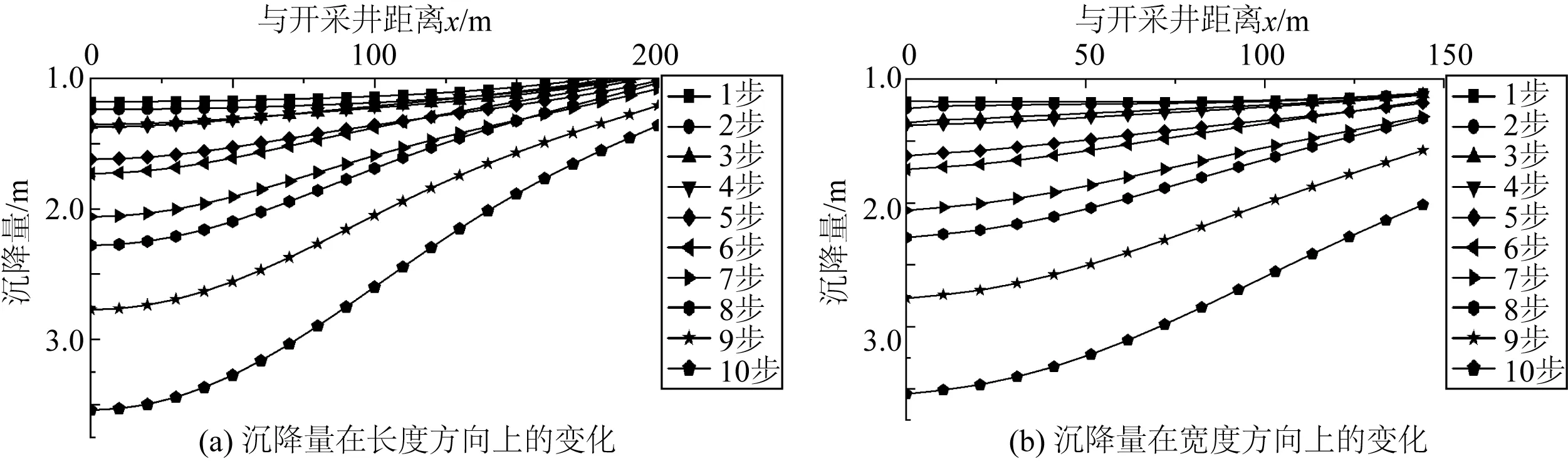
图6 海床沉降量在模型长度和宽度方向上的变化Fig. 6 Variation of seabed subsidence with the length and width of the model

表3 开采过程中开采井处的海床沉降量Tab. 3 Subsidence of seabed at the mining well in mining process

为验证该模型模拟结果的准确性和适用性，与基于“热-水动力-机械耦合”模型模拟的水合物开采引起的海床沉降情况进行对比和验证。金光荣等[9]通过使用TOUGH2Biot模拟器，扩展了Biot合并模型，从而得到了用于水合物开采的“热-水动力-机械耦合”模型，通过改变开采井底部压力，获得了神狐海域天然气水合物开采过程中海床不均匀沉降的规律。

将“生死单元”法获得的海床沉降量与文献进行对比，结果如图7所示，图7(a)为“生死单元”法海床沉降计算结果，图7(b)为金光荣等[9]通过降压法开采水合物得到的海床沉降曲线。图7(a)分别为第5、第7和第9步开采时海床沉降的结果，海床最大沉降量分别为1.621 m、2.068 m和2.767 m，沉降发生的主要区域位于开采井400 m范围内；图7(b)分别为开采时间为第0.5、第1和第2年时海床沉降的结果，海床最大沉降量分别为1.52 m、1.80 m和2.50 m，沉降发生的主要区域位于开采井500 m范围内。两种结果较为接近，海床的最大沉降都位于开采井处，当海床与开采井的距离增大时，沉降量都会逐渐减小。将图7(a)中的曲线拟合到图7(b)中，可以看出文中“生死单元”法模拟的水合物开采引起的海床表面沉降形态与“热-水动力-机械耦合”法模拟的海床表面变形形态能够很好的吻合，海床沉降的数值也很接近前人的研究成果。验证了通过使用ABAQUS中单元生死功能模拟水合物开采进而引发海床沉降这一方法是可行的，以该模型获得的海床沉降规律作为管道受力分析的边界条件是合理的。

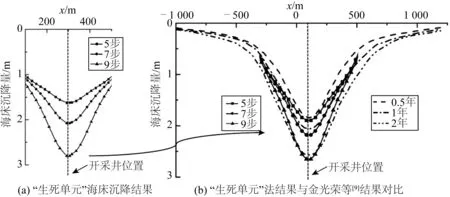
图7 海床位移曲线Fig. 7 Displacement curve of seabed

4 海床不均匀沉降引起的管道力学性能变化

基于获得的海床沉降规律，研究海床沉降对管道造成的力学行为变化，分析管道的竖向位移、曲率和弯矩、应力应变分布、管道悬跨等问题。

4.1 管道竖向位移

在水合物开采过程中，管道竖向位移随着海床的沉降发生变化。图8(a)为管道位置变化示意，图8(b)为每一开采步的管道竖向位移量，表4为开采过程中开采井处管道的沉降量。结果显示，管道在开采井附近的竖向位移最大，为3.407 m，当管道位置远离开采井时，由于海床的沉降量逐渐减小，管道的竖向位移也逐渐减小。管道的位移曲线关于开采井位置对称且沉降主要发生在开采井周围400 m范围内，沉降的最大值总是出现在开采井处。这一形态与海床的表面沉降形态是一致的。

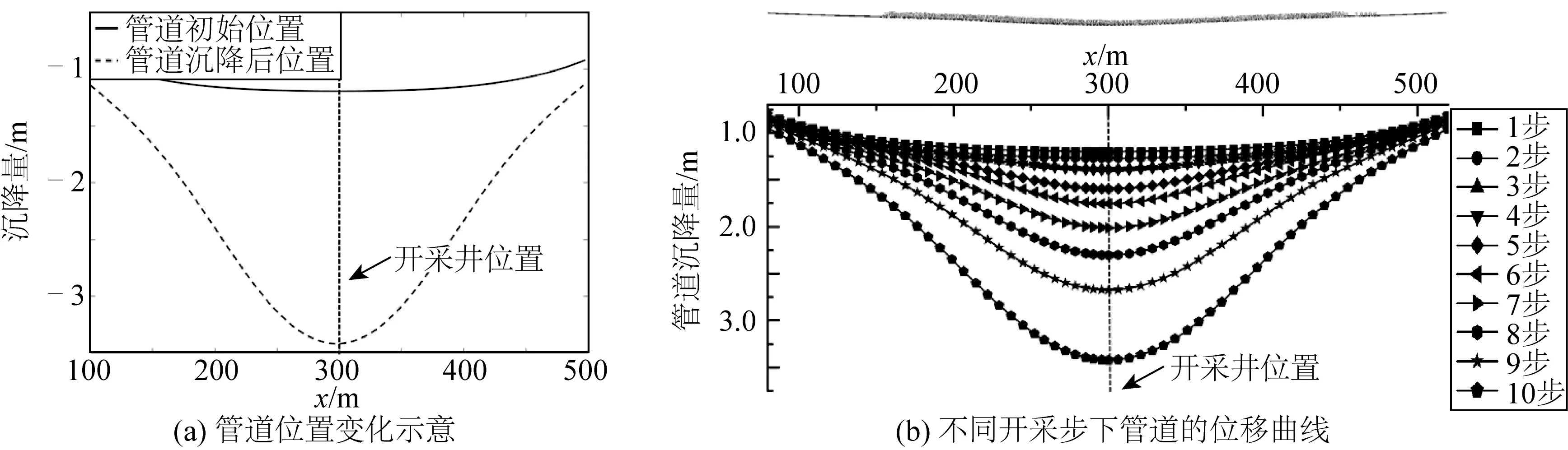
图8 管道的竖向位移Fig. 8 Vertical displacement of pipeline

表4 开采过程中开采井处的管道沉降量Tab. 4 Subsidence of pipeline at the mining well in mining process

4.2 管道的曲率及弯矩分布

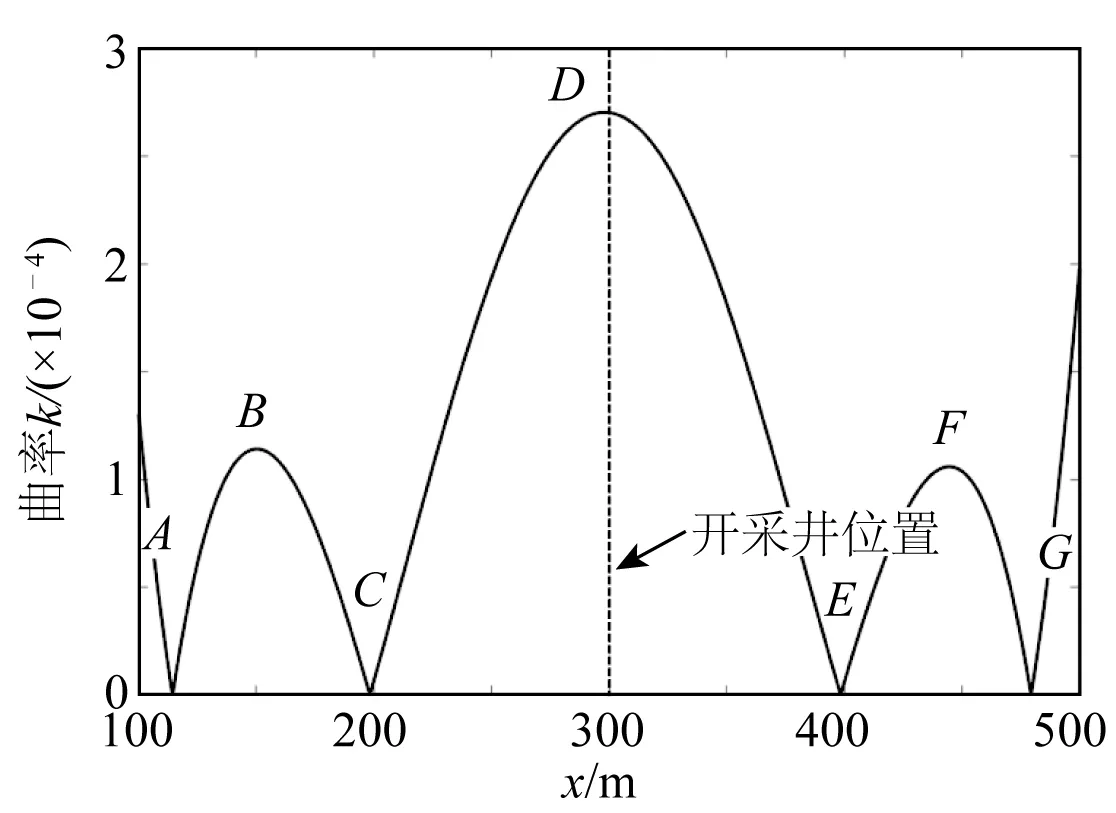
图9 管道曲率Fig. 9 Curvature of pipeline

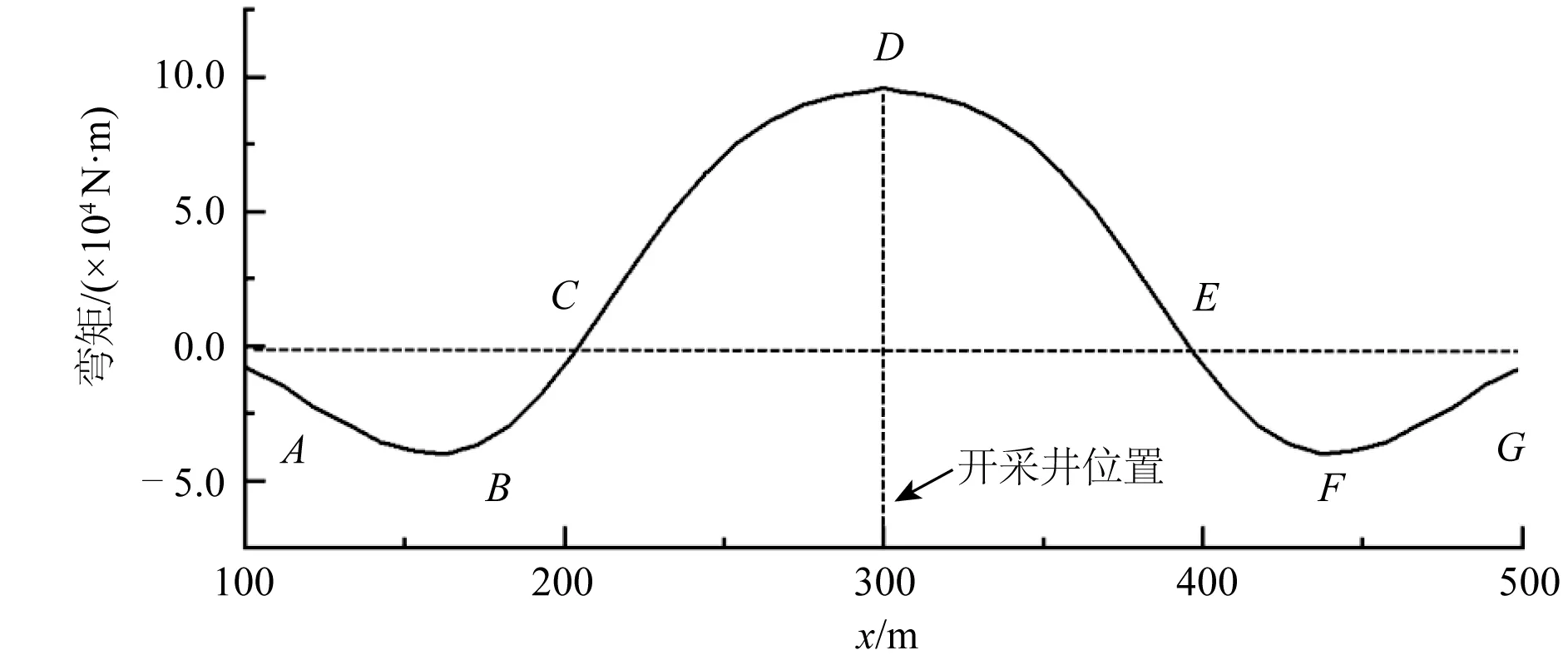
图10 管道弯矩Fig. 10 Bending moment of pipeline

4.3 管道的应力应变分布

由于天然气水合物的开采导致管道发生较大的沉降，尽管沉降的跨度较大，但是依然会对管道的应力应变造成影响。由于海床沉降主要发生在开采井附近区域，距离开采井附近150 m区域内的沉降量较大，对管道应力应变的影响更为显著，因此只需选择该区域进行分析即可。如图11(a)所示，管道应力和应变的最大值均出现在管道中点的底部。每一步开采后，管道的最大应力和应变值如图11(b)所示，随着水合物开采范围的扩大，管道的最大应力和应变都随之增加，应力值的范围为9.97～24.37 MPa，应变值的范围为4.38×10-5～1.17×10-4。

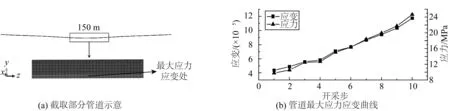
图11 管道的最大应力、应变Fig. 11 Maximum stress and strain of pipeline

为了探究该150 m范围内管道上应力应变随水平位置的变化趋势，须对每一步开采所对应的管道的应力应变进行数据提取，得到的结果如图12所示。

图12 开采过程中管道的应力、应变分布Fig. 12 Stress and strain distribution of pipeline in mining process

如图12所示，每一步开采后，管道的应力应变随水平位置的变化趋势是一致的，当管道位置靠近开采井时，管道的位移和变形逐渐增大，导致管道的应力应变逐渐增大；当管道位置远离开采井时，管道的位移和变形逐渐减小，导致管道的应力应变逐渐减小。管道的应力应变曲线关于开采井位置对称且最大值总是出现在开采井处。从图11和图12可以看出，天然气水合物开采导致海床的不均匀沉降会改变管道的应力应变状态，开采范围的扩大会导致管道内部的应力和应变逐渐增大，但是其数值都还在安全范围以内，因此水合物的开采对管道的应力应变影响相对较小，在应力应变的角度上，管道是安全可靠的。

4.4 管道的悬跨

在水合物开采过程中，管道虽然随着海床的沉降发生竖向位移，但由于管道本身具有弯曲刚度且受到轴向拉力的约束，在竖向位移发生到一定程度后，则不再发生变化。因此，当海床的沉降量达到一定值时，管道不再继续沉降，而是与海床发生分离，在海床表面形成悬跨，且逐步增大，如图13所示。在开采过程中海床和管道的相对位移变化量如图14所示。如图14(a)所示，天然气水合物开采在前4步即开采范围在80 m以内时，海床与管道的最大沉降量相等，这表示海床与管道是始终接触的，当天然气水合物开采到第5步即开采范围达到100 m时，海床与管道的最大沉降量分别为1.621 m和1.576 m，出现0.045 m的悬空，此时海床和管道已发生分离。随着开采范围的继续增大，海床与管道之间的悬空距离整体呈上升趋势，如图14(b)所示。当海水流经悬跨管道时，在一定流速条件下，悬跨管道两侧会出现旋涡，并以一定的频率交替脱落，从而在管道表面形成周期载荷，将会使悬跨管道在顺流方向及横流方向上发生振动，即涡激振动，很可能对海底管道造成疲劳损伤乃至破坏[13-15]。

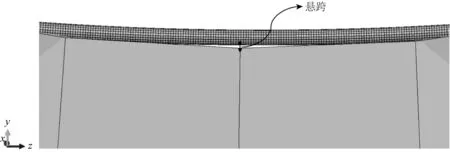
图13 管道与海床分离产生悬跨(开采步10)Fig. 13 Suspension span caused by separation of pipeline and seabed (Mining step 10)

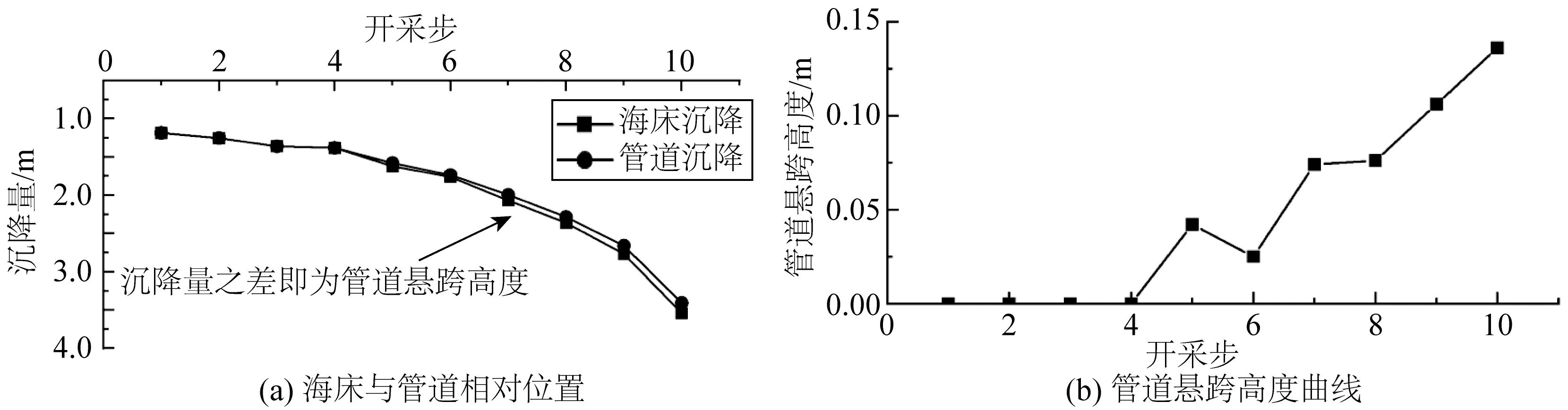
图14 开采过程中管道和海床的沉降量及悬跨高度变化Fig. 14 Change of seabed subsidence and height of suspension span of pipeline during mining process

5 结 语

经过研究和计算分析，可以得到以下结论：

1) 有限单元中“生死单元”法可以等效模拟天然气水合物开采过程中海床的变形规律，为海底管道的沉降分析提供边界条件，对于模拟海底管道在海床沉降边界下的安全校核有重要的指导意义。

2) 天然气水合物开采引起的海床沉降区域主要集中在开采井附近400 m的范围内，其对管道的应力、应变、位移、曲率和弯矩均产生影响。由海床沉降引起的管道应力应变基本处于弹性范围内，不会造成管道本身的强度破坏；但是当海床沉降达到一定程度时，铺设在开采区内的海底管道将与海床发生分离，形成悬跨，并引发涡激振动风险，对管道造成疲劳破坏。

3) 基于天然气水合物“单井开采”模型进行海床沉降研究，与实际工程中的“多井联合开采”模式仍有一定差距。后续研究中可进一步考虑多井联合开采工况下海床的变形规律及其影响，为天然气水合物的大规模开发提供技术支撑。