钢管脐带缆扭转平衡设计

牛学超，祝庆斌，潘 盼，邵鹏进，胡 明，谢书鸿

(中天科技海缆有限公司，江苏 南通 226015)

钢管脐带缆通常是一种由超级双相不锈钢管、电缆、光缆及填充单元等通过非黏结螺旋缠绕而组成的复合缆，其在水下生产系统中有着重要的应用。但由于钢管具有较大的刚度，相较于普通电缆，钢管脐带缆在制造、流转、存储、运输、安装和在位运行时对力学性能有更高的要求。尤其在受到拉伸、弯曲和扭转载荷时，钢管脐带缆极易出现扭转失效[1]。Shibu等[2]认为缆在受到拉伸载荷时，螺旋缠绕的结构会产生扭矩，缆会因此而旋转，从而使得部分铠装钢丝松弛而部分铠装钢丝收紧，缆的力学性能将受到影响；而且如果缆的长度较长且限制其旋转，当拉力衰减时，产生的扭矩会让缆发生扭转失效。为了防止缆扭转失效，钢管脐带缆必须进行扭转平衡设计。

线缆的扭转平衡设计有解析法和有限元方法。解析法主要基于缆的线弹性矩阵方程(详见第一节)，通过推导不同条件下刚度矩阵方程来进行扭转平衡设计。Hruska[3]首先基于螺旋缠绕钢丝的纯几何关系，推导了钢丝在拉伸载荷下的刚度矩阵方程，其忽略了单根钢丝的弯曲刚度和扭转刚度。Machida等[4]研究了每根钢丝的弯曲刚度和扭转刚度对刚度矩阵元素的影响，对刚度矩阵方程进行优化。Sathikh等[5]则展示了一种各向同性线弹性模型，得出了钢丝在拉伸、扭转和弯曲载荷下的刚度矩阵方程。虽然这些解析法分析模型简单且易于使用，但是考虑到钢丝材料、空间几何布局和挤压、摩擦的复杂性，这些分析模型的有效性有限[6]。Ghoreishi等[7]建立了“1+6”结构的钢丝绳有限元模型，计算其在拉伸载荷下的结果并与解析法结果进行对比，研究显示钢丝绞合角度小于20°时解析法较为有效。Nawrocki等[8]建立涉及中心钢丝运动的钢丝绳有限元模型，对其施加拉伸和弯曲载荷，研究发现钢丝的绕轴转动和相互滑动主导了钢丝绳的力学性能。Kim等[6]分别建立了2层和3层钢丝的钢丝绳梁单元有限元模型，研究了梁单元有限元模型在精度和效率方面的优势，并提出了一种扭转平衡设计方法。

但是由于缺乏试验数据，尤其对于直径较大的线缆通常需要订制特殊测试设备。因此，上述分析模型为了验证各自的有效性，将缆芯简化为一个实心圆柱，以此来与Utting的试验数据进行对比[9]。然而，钢管脐带缆结构复杂，各种材料的功能单元多，摩擦情况复杂；而且螺旋缠绕的钢管数目多，刚度大，忽略缆芯对扭转平衡的影响而将其简化为一个实心圆柱并不准确。基于某型钢管脐带缆，建立实体单元有限元模型，通过控制变量法研究模型在拉伸载荷下的扭转平衡设计方法。并根据有限元方法计算结果制造了实物钢管脐带缆，对其扭转平衡性能进行测试，测试结果显示钢管脐带缆是扭转平衡的，从而验证了有限元设计方法的有效性。

1 背景理论

暂时忽略缆芯对扭转平衡的影响，研究影响缆扭转平衡的关键变量。对螺旋绞合的缆而言，拉伸运动和扭转运动是耦合的，其线弹性矩阵方程可由式(1)表示：

(1)

其中，FS是轴向拉力，MS是扭矩，ε是轴向拉力下的应变，γ是单位长度扭转角Δθ/L，Fε、Fφ、Mε、Mφ是刚度矩阵元素。

在对称的线弹性模型中，Fφ=Mε。如果缆是扭转平衡的，MS和γ将为0。由此，Mε=0。

采用Sathikh等[5]展示的各向同性线弹性模型，则Mε可表述为：

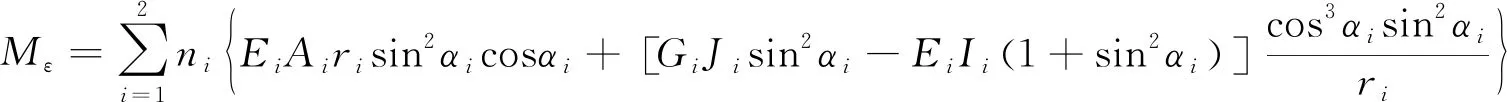
(2)

其中，ni是i层的钢丝数，ri是i层钢丝的螺旋半径，αi是i层的绞合角，Ai是绞合钢丝的截面积，Ei是绞合钢丝的弹性模量，Gi是绞合钢丝的剪切模量(在计算中令Gi=E/2(1+ν)，ν是钢丝泊松比)，Ii、Ji分别是绞合i层钢丝的截面惯性矩和截面极惯性矩。

由上述公式可知，螺旋缠绕结构的数量、材料、横截面、螺旋半径和绞合角度对缆的扭转平衡产生了影响。然而对于钢管脐带缆，螺旋缠绕结构的材料、数量、横截面、螺旋半径这些参数通常是确定的或设计时优先程度要高于扭转平衡。因此，选择螺旋结构的绞合角度作为唯一变量，进行钢管脐带缆的扭转平衡设计。

2 有限元方法

脐带缆在受力时各功能单元之间可以相对滑动，一方面赋予了脐带缆灵活性，另一方面增加了分析的复杂性[10]。有限元方法相对于解析法，可以更有效模拟脐带缆各个单元在受力时的相互接触、摩擦。文中构建了实体单元有限元模型，使用控制变量法进行钢管脐带缆扭转平衡设计。

2.1 确定脐带缆缆芯节距

钢管脐带缆缆芯节距主要取决于超级双相不锈钢钢管。首先，钢管在成缆时，从直管变成螺旋管会产生一定应变，而且绞合角度越大(即节距越小)应变越大，按照行业惯例，成缆过程钢管应变应低于2%。其次，钢管绞合角度越小(即节距越大)，其在整根脐带缆(包括铠装钢丝)承受拉伸载荷时承担的拉伸载荷比例越大[11]，钢管应该基于承受的最大拉伸载荷进行强度校核。文中所述脐带缆缆芯节距为2 m，建立缆芯有限元模型如图1所示。

图1 脐带缆缆芯有限元模型Fig. 1 FE model of umbilical core

将缆芯的两端面分别约束到一个点上，以便于施加载荷和约束，以及提取计算数据结果。然后将缆芯模型一端全约束，另一端设置为自由旋转端，并承受轴向拉力。

对自由旋转端施加120 kN拉力并提取旋转角度，以0.3 s的有限元模拟时长进行计算。计算结果如图2所示，缆芯应力云图显示，螺旋缠绕的钢管是主要承力单元，并且缆芯在拉伸载荷下出现一定的扭转，扭转角度曲线如图3所示。由此可见脐带缆缆芯存在扭转不平衡，不能因为节省计算时间，提高效率将缆芯简化为一实心圆柱。

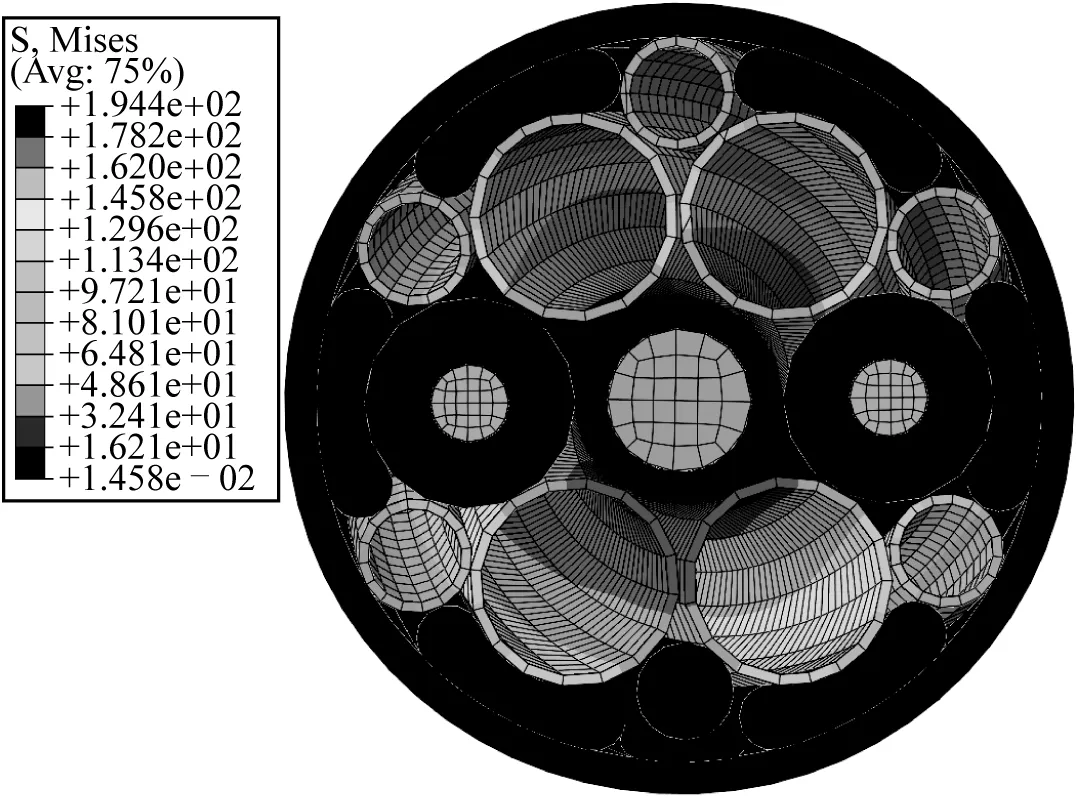
图2 轴向拉力下缆芯应力云图Fig. 2 Stress nephogram of umbilical core under tension load

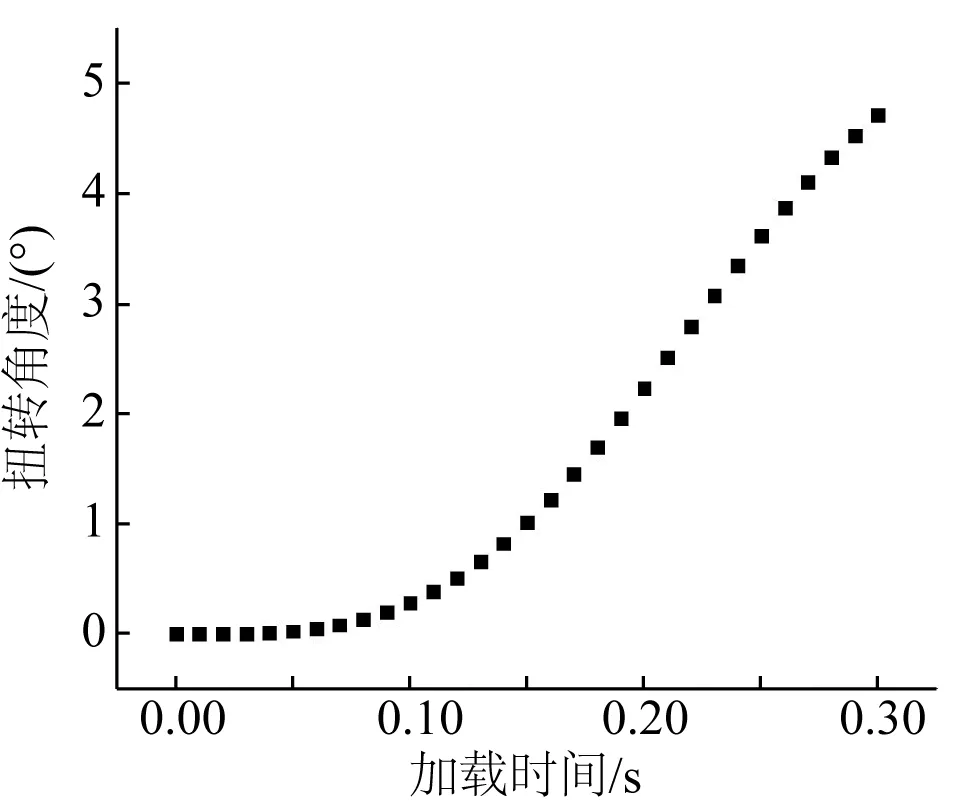
图3 轴向拉力下缆芯扭转角度和加载时间关系曲线Fig. 3 Relationship curve of rotation angles and simulation time for umbilical core under tension load

2.2 确定脐带缆第一层铠装钢丝参数

铠装钢丝可有效用于保护脐带缆内部单元，增强缆的机械性能，控制直径与重量比值来优化缆的海底稳定性，避免涡激振动等。因此，在确定钢丝形状、直径、材料和绞合角度等参数时有诸多考虑因素。文中所用第一层铠装钢丝参数见表1。

表1 第一层铠装钢丝参数表Tab. 1 Parameters of first layer armor wires

2.3 建立第二层铠装钢丝不同绞合角α2的有限元模型

钢管脐带缆使用两层规格相同的钢丝异向绞合，并且确定第二层钢丝根数为62。接下来以第二层铠装钢丝的绞合角α2为唯一变量进行有限元计算分析，以获得在拉伸载荷下第二层铠装钢丝绞合角度与缆扭转角度的对应关系。

图4 脐带缆有限元模型Fig. 4 FE model of the umbilical cable

由于第一层铠装钢丝绞合角度为18°，而且绞合方向为左向，于是分别建立第二层铠装钢丝绞合角为10°、15°、20°、25°、30°，绞合方向均为右向的有限元模型如图4所示。为了提高计算精度，使用三维实体各向同性的线性减缩积分单元建模，模型采用六面体网格进行划分。为了节约计算时间，一方面将性能接近的交联聚乙烯，中密度聚乙烯，高密度聚乙烯统一定义为高密度聚乙烯；另一方面非螺旋缠绕结构或弹性模量较低的材料划分网格时使用粗糙网格，铠装钢丝和钢管使用精细网格。

2.4 设置不同材料摩擦系数

钢管脐带缆作为非黏结螺旋缠绕结构，在受到拉伸、弯曲和扭转载荷时，各功能单元有一个突破静摩擦到动摩擦的过程。在此过程中，钢管脐带缆的拉伸刚度、弯曲刚度和扭转刚度值有较为明显的变化[12]。因此，对脐带缆机械性能分析而言，摩擦系数是一项关键参数。使用试验所得的摩擦系数见表2。

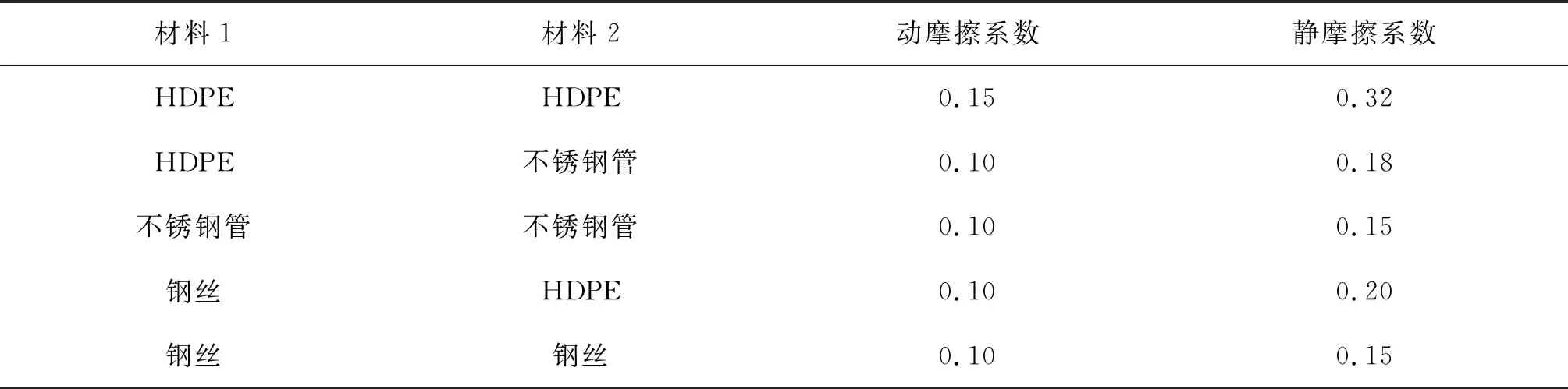
表2 各材料间摩擦系数Tab. 2 Friction factors of materials

2.5 设置边界条件并施加载荷

扭转不平衡的缆，如果一端全约束，另一端可以自由旋转，则在轴向拉伸载荷下，自由端会产生一个扭转角度。而且拉伸载荷越大，扭转角度越大。因此，如果将第二层铠装钢丝绞合角作为横轴，将缆在轴向拉伸载荷下的扭转角度作为纵轴，那么将第二层铠装钢丝绞合角度不同的缆在相同拉伸载荷下的扭转角度拟合为一条直线，则直线与横轴的交汇点应为缆在扭转平衡时第二层铠装钢丝绞合角度。给缆施加3种不同的拉伸载荷，拟合出3条直线，即可得到3个交汇点。那么可以认为这3个交汇点的平均数就是第二层铠装钢丝的最优绞合角度。将缆的两端面分别耦合至一集中点，一端全约束，另一端设置为自由旋转端并分别承受40 kN、80 kN、120 kN的轴向拉力，提取自由旋转端的扭转角度。

2.6 结果分析

图5为脐带缆受轴向拉伸载荷下应力云图，可见钢管和铠装钢丝均为主要承力单元。这说明螺旋缠绕的钢丝和钢管在拉伸载荷下都会产生扭矩，因此不能将钢管脐带缆缆芯简化为一实心圆柱。对不同绞合角度脐带缆有限元模型在承受不同拉伸载荷下的扭转角度做拟合线，如图6所示。由此可见当绞合角α2为14°左右时，缆在不同拉伸载荷下达到了扭转平衡。因此14°即为钢管脐带缆在扭转平衡时第二层铠装钢丝的最优绞合角度。

图5 轴向拉力下脐带缆应力云图Fig. 5 Stress nephogram of umbilical cable under tension load

图6 扭转角度和绞合角α2在拉伸载荷下的关系图Fig. 6 Relationship of rotation angles and stranded angle α2 under tension load

3 扭转平衡试验

根据第2节的结论，以第二层铠装钢丝绞合角度为14°制造了脐带缆。基于ISO13628-5规范[13]对钢管脐带缆进行扭转平衡测试。

试验原理如图7所示。缆的一端为固定端，连接液压拉力机，限制其旋转；另一端为自由端，连接退扭器，在受拉力时可自由旋转。考虑到端部效应，在距离两端锚固一个成缆节距范围外安装角度传感器，该传感器固定在缆外护套上方，随着缆旋转。为了防止缆自身重量对试验结果造成影响，在缆下面放置支撑，使得缆轴心与受力在同一直线上。

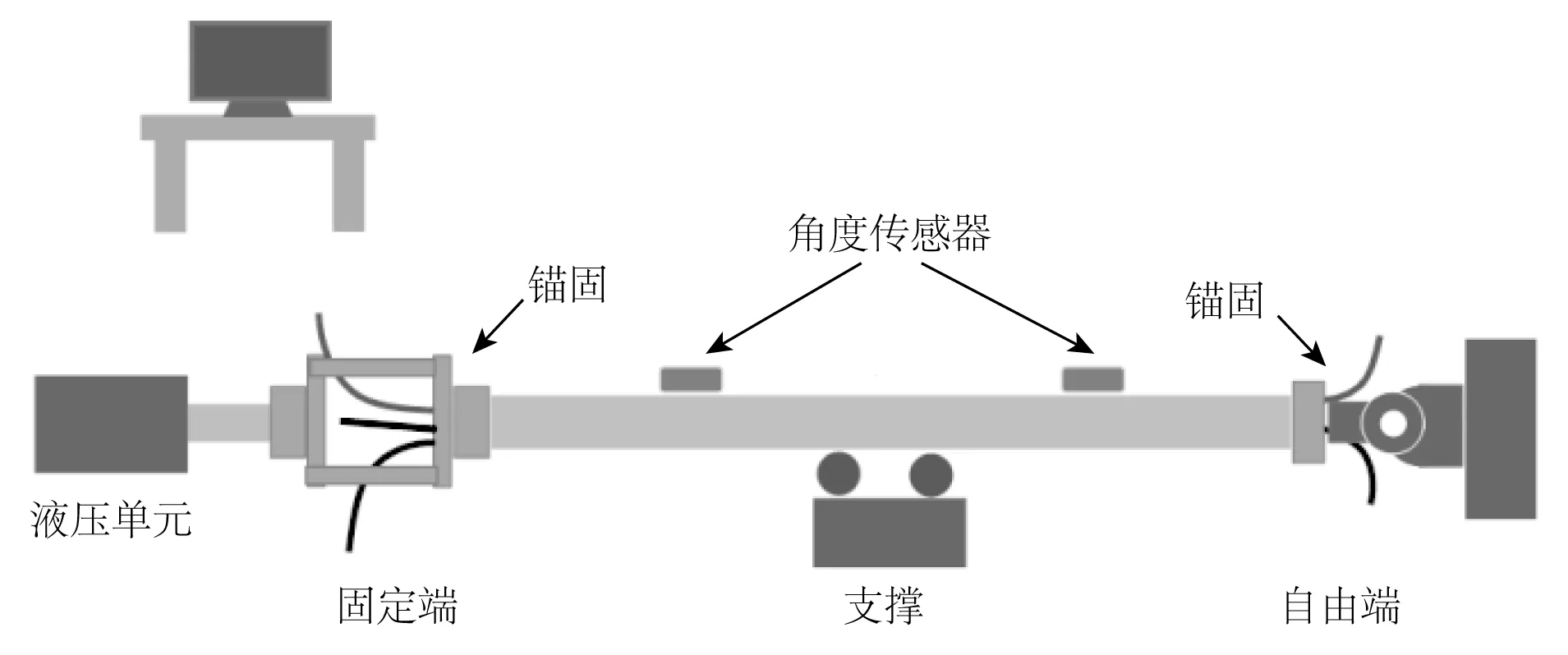
图7 拉伸载荷下测量扭转角度原理Fig. 7 Schematic diagram of rotation angle measurement under tension load

脐带缆扭转平衡特性用单位长度扭转角γ表示，其公式为：

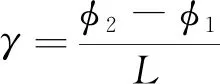
(3)

其中，L是两角度传感器之间的距离，是一固定值，为2.5 m；转角φ1为靠近固定端的角度传感器的示数；转角φ2为靠近自由端的角度传感器的示数。

对缆施加初始载荷20 kN，然后将两个转角传感器示数归0，以避免系统测量误差。加载拉伸力值按照20 kN的梯度增加到200 kN，然后按照20 kN的梯度卸载至20 kN。每个梯度持续60 s，以便记录转角数据。载荷施加过程如图8所示。试验过程记录如表3所示。

图8 脐带缆承受的拉伸载荷Fig. 8 Tension load on umbilical cable

表3 拉伸载荷下脐带缆的单位长度扭转角Tab. 3 Rotation angles per meter of umbilical cable under tension load

试验结果显示，脐带缆在不同拉伸载荷下，单位长度旋转角最大为0.036°/m，远小于行业惯常接受标准0.5°/m。由此可知脐带缆是扭转平衡的。

4 结 语

建立钢管脐带缆实体单元有限元模型，采用控制变量法进行扭转平衡设计。并对实物脐带缆进行扭转平衡测试。得到以下结论：

1) 钢管脐带缆在受到轴向拉伸载荷时，钢管作为主要承力单元会产生一定的扭矩，因此不能在计算时将脐带缆缆芯简化为一实心圆柱。

2) 钢管脐带缆在扭转平衡设计时，采用控制变量法，以第二层铠装钢丝的绞合角为变量，建立实体单元有限元模型，计算在拉伸载荷下有限元模型的扭转角度，并将数据拟合成直线，该拟合线与绞合角度所成横轴的交汇点即为第二层铠装钢丝的最优绞合角，如此可有效避免大量的计算。

3) 对实物钢管脐带缆进行扭转平衡测试，测试结果显示脐带缆是扭转平衡的，验证了该有限元方法在钢管脐带缆扭转平衡设计时的有效性。