正定二次型问题解法举隅

江苏省无锡市第一中学 (214031) 钱 铭 江南大学理学院 (214122) 谢广喜

数学竞赛题思维容量大，解竞赛题有助于学生创造性思维的培养.有些知识点常考常新，在命题者眼中，它们是提高学生数学核心素养的良好载体，本文试举例以分享.

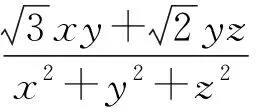
评注:从根本上来说，这类问题的背景属于高等代数/线性代数中的正定二次型问题.

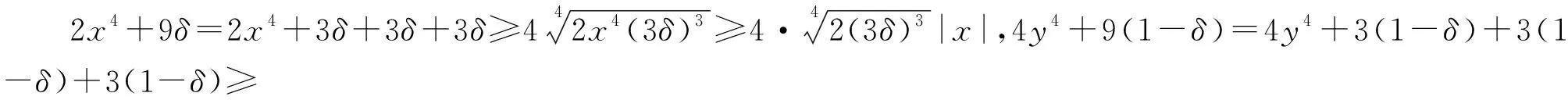
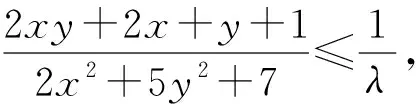
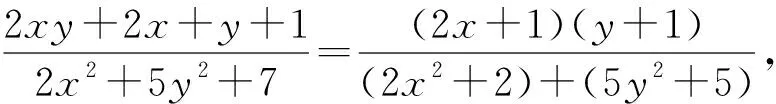
评注：发现λ=2，(*)式即为2[x-(y+1)]2+3y2-6y+3≥0，也即有2[x-(y+1)]2+3(y-1)2≥0，即x=2,y=1时取得等号.

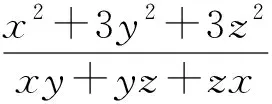
仿照上述例题，可解决题目：若实数a,b,c满足a2+b2+c2=1，则3ab-3bc+2c2的最大值是.(2015浙江省五校联考第17题)

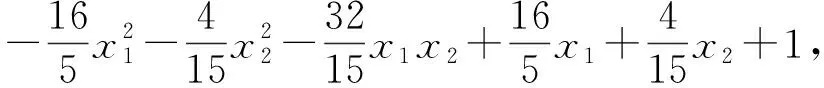
评注：这道题是带有附加条件的多元最值问题，通常的主元配方思想是基本的切入点，尤其要注意不等式取最值时的等号情形验证，否则可能得到错误答案.