一道多元变量最值高考题的多角度探究

江苏省苏州市吴江盛泽中学 (215228) 周伟芯 沈惠华

多元变量最值问题是高考命题中的“常客”，一般出现在选择题或填空题中，这类问题题干简练，解法却精彩纷呈，不同的解法往往可以帮助学生构建高中数学的知识网络，提升学生的数学能力.本文撷取一道2020年高考数学江苏卷上一道题目加以探究，供大家参考.

题(2020年高考江苏卷第12题)已知5x2y2+y4=1(x,y∈R)，则x2+y2的最小值是.

说明：江苏卷中共有14个填空题，前9个一般没有难度，属于送分的基础题，第10-12题具有一定难度，属于中档题，而第13和14题属于填空题部分较难的压轴题.本题属于中档题，考查考生的逻辑推理和数学运算的核心素养，考查考生数学解题中的转化能力.本题从不同角度入手，可以得到不同的解法.

一、从函数的角度入手

从函数的角度入手，就是通过消元或其它手段把原问题变成一元函数的最值问题.

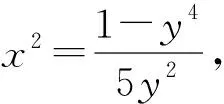
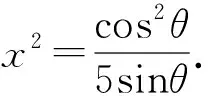
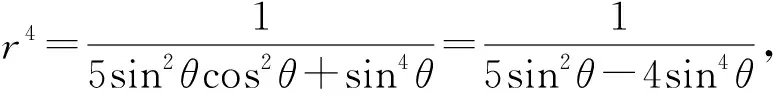
二、从不等式的角度入手

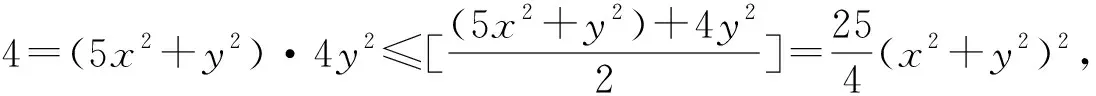
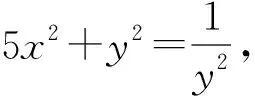
三、从方程角度入手

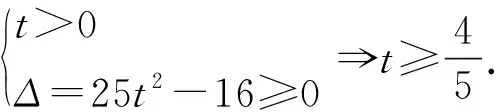
四、从曲线与方程的角度入手

解法8：(经过换元，将原问题转化为直线与二次曲线的位置关系问题)令x2=X>0,y2=Y>0，则条件等式5x2y2+y4=1即为方程5XY+Y2=1，它表示位于第一象限的二次曲线；目标函数x2+y2即为X+Y，令它的值为m，则方程X+Y=m表示这条直线位于第一象限的部分.

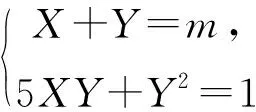
众所周知，高考题具有选拔功能，思维层次不同的考生往往得到不同的解法，而从不同角度出发思考也往往会产生不同的解题效果，或许解法比较繁琐，或许解法比较简洁，但无论哪种解法都蕴含着丰富的数学思想，只要适合学生，它们都是好方法.从以上高考题的八种解法中，我们可以看出，通过一道题的“一题多解”，可以撑起高中数学的“一片天”，可以编织知识与方法的“关系网”，这或许就是高中数学解题教学的“最高境界”.