基于相参累积预处理的空间谱估计方法

余华兵， 郑恩明， 陈新华

(1.北京神州普惠科技股份有限公司, 北京100085; 2.中国科学院 声学研究所, 北京100190)

近年来，具有自适应能力的最小方差无畸变响应空间谱估计(MVDR)方法在声纳、雷达和通讯等领域获得了广泛应用[1-2].然而，现有的MVDR方法对接收阵拾取的空间数据平稳性要求较高，在空间数据稳定性较差时，将无法稳定获取协方差矩阵的估计值，进而影响权向量最优解的求取及空间谱估计的效果，限制了其在实际应用中的发展[3-4].

为了克服空间数据平稳性对MVDR方法的影响，文献[5-6]采用空间平滑方法和对角加载技术，通过对协方差矩阵构造Toeplitz矩阵或对协方差矩阵对角线加载相应常数实现协方差矩阵的解相关，提高了MVDR方法的稳定性.文献[7]通过构造增广数据矩阵并对其进行奇异值分解求解增广矩阵逆，改善了MVDR方法对相干信源波达方向估计的性能.文献[8]通过对角减载技术在一定程度上降低了对角加载技术带来的信干噪比损失.文献[9]通过小波变换实现了对相干信号波达方向估计.文献[10]提出一种基于自回归(AR)模型的MVDR方法，通过阵元信息重复利用方法在保持分辨率不变的情况下提高了稳定性.文献[11]在时域上改善了权向量优化的估计方法.

虽然，以上研究成果有效地提高了MVDR方法的稳定性，但均未充分利用各传感器的相位信息，也未考虑在协方差矩阵构建之前就进行相应的变换处理以提升稳定性.本文提出一种基于相参累积预处理的空间谱估计方法，记作CCPMVDR方法.该方法可以通过时频分析处理，改变构建协方差矩阵的数据来源，在短时间内获得足够多的时间采样点数，在一帧数据内通过时域多个采样点累积实现满秩协方差矩阵的稳定获取.同时，通过对接收阵拾取数据在子阵维度上进行相参累积处理，形成一次指数函数等列式求和运算，进一步降低了空间谱估计对空间数据的要求.

1 MVDR方法的空间谱估计

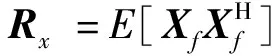
(1)

式中：θ为空间扫描角度；B(f,θ)=[ej2πfτ1ej2πfτ2… ej2πfτ2N-1]为导向权向量，τn=(n-1)dcosθ/c，1≤n≤2N-1为接收阵所含传感器编号，c为声速，d为接收阵相邻传感器间距.

然后，在θ处采用权向量最优解Wopt实现空间谱估计，获得相应的估计值PMVDR(f,θ).

PMVDR(f,θ)=

(2)

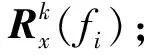
(3)

2 CCPMVDR方法的空间谱估计

2.1 基本原理

由FFT分析可知，一帧多个时域采样点数据经过FFT后，在频域同一频点只包含单个频域数据，利用单个频域数据求取协方差矩阵时，容易出现非满秩现象.对此，采用时频分析处理方法，通过对一帧多个时域采样点数据的累积，提升协方差矩阵的稳定性.

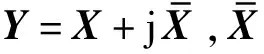
令φ(t)为一小波函数，首先对其作FFT可得其频谱函数ψ(w)，然后对ψ(w)的正频率部分进行逆FFT(IFFT)，可得φ(t)对应的复解析形式φ(t)为

(4)

最后，采用复解析小波φ(t)对接收阵拾取数据X进行卷积处理，可得X的复解析形式为

(5)

通过选择小波函数参数(如带宽参数、中心频率和尺度伸缩因子)，可在对接收阵拾取数据实现复解析变换的处理中抑制分析频带以外的背景噪声，具体证明可参考文献[14].

其次，依据空间方位与各传感器数据之间的相位差关系[15-16]，对接收阵各传感器拾取数据进行处理，获得的N组数据为

(6)

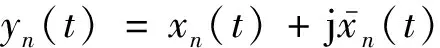
根据相位与时延之间的关系，在θ上对各传感器的时域复解析数据yn(t)按τn=(n-1)dcosθ/c进行时延补偿，可得经时延补偿后的数据为

yn(t+τn)=

|xn(t)|exp[j(γ0+γτ)]=

|xn(t)|exp(jγ0)exp(jγτ)=

yn(t)exp(jγτ)

(7)

式中：γ0为目标信号引起的传感器数据之间的相位差；γτ为等同于时延补偿的相移因子.

由式(7)可知，对复解析数据的时延补偿等同于相移补偿.在θ处对式(6)中Z1，Z2，…，ZN所包含的数据进行时延处理，获得的N组时延后的数据为

(8)

(9)

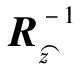
(10)

m=1,2,…,N

(11)

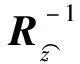
CCPMVDR方法通过对接收阵拾取数据进行时域复解析变换和相参累积预处理，形成了两次指数函数等列式求和运算处理，提高了空间谱估计的稳定性.

2.2 实现流程

由理论分析可知，CCPMVDR方法可分为如下步骤实现.

步骤1对接收阵拾取数据进行复解析小波变换和分帧处理(相邻两帧之间按0.5倍帧长度进行重叠处理)，得到K帧复解析数据Y，并令处理数据帧号k=1；

步骤2根据式(6)对第k帧复解析数据Y分组处理；

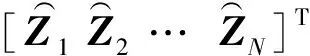
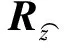
步骤7对K个空间谱估计值进行累加处理，获得本次处理的最终空间谱估计值.

(12)

2.3 性能分析

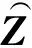
(13)

l=1,2,…,N;k=1,2,…,N

式中：sn为第n个传感器拾取的目标信号；vn为第n个传感器拾取的背景噪声；H为共轭运算.

当空间目标所在方位θ0与θ一致时，式(13)可进一步表示为

(14)

i=1,2,…,N;k=1,2,…,N

式中：s0为原始目标信号；v0为背景噪声统一表示值.

由式(14)可知，经式(6)～(9)处理后，MVDR方法和CCPMVDR方法所用协方差矩阵中的目标信号和背景噪声能量含有量可表示为

(15)

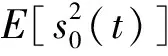
3 数据处理分析

3.1 数值仿真分析

为进一步验证CCPMVDR方法的空间谱估计性能，进行如下数值仿真分析.

3.1.1单目标情况 仿真条件：采用32元相邻阵元间距为0.5 m的线列阵作接收阵，目标信号频率为 1 400～1 600 Hz，目标信号长度为0.01 s，目标方向为90°，目标信号与背景噪声信噪比记为SNR，系统采样频率为20 kHz，一次处理数据长度为1 s.MVDR方法和对角加载MVDR(DLMVDR)方法具体处理过程如下：首先对2×104个采样数据分78帧处理(单帧数据长度为256个采样数据，帧与帧之间重叠128个采样数据)，对每帧数据做FFT分析；最后对 1 400～1 600 Hz频带各频点作协方差矩阵估计、最优权向量解和空间谱估计，DLMVDR方法对角加载量为噪声子空间对应的最小特征值；CCPMVDR方法通过复解析小波变换选取 1 400～1 600 Hz频段，然后采用相同的分帧处理方法按2.2节的流程实现.

SNR=-30～0 dB情况下，由MVDR、DLMVDR和CCPMVDR方法通过200次独立统计所得的不同信噪比下的目标方位估计均方误差(RMSE)如图1所示.

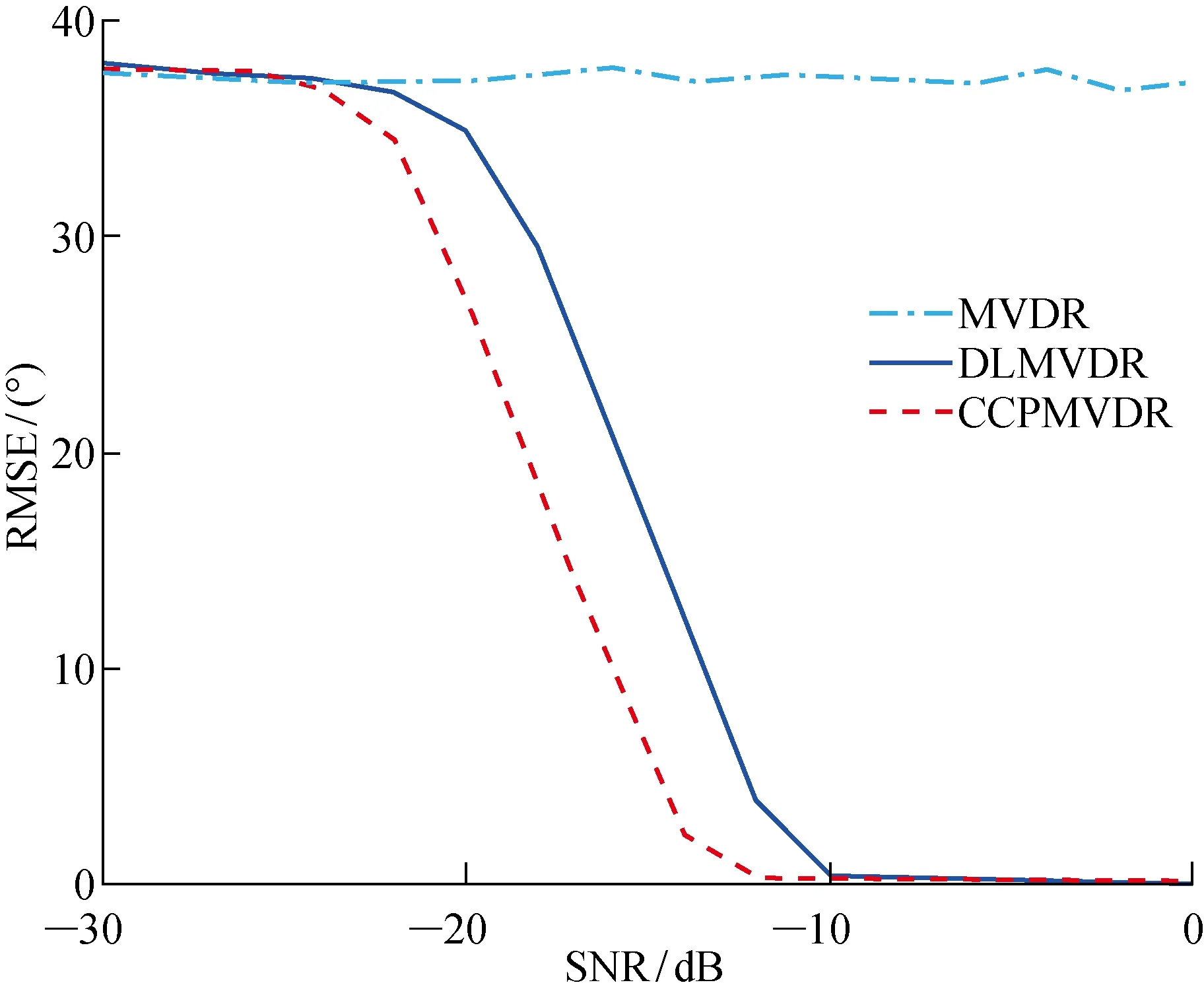
图1 不同SNR下，3种方法的RMSE

由图 1的仿真结果可知，相比MVDR和DLMVDR方法，CCPMVDR方法对目标信号稳定的要求得到了有效的改善.在该仿真条件下，由于信号长度小于一帧数据长度，一帧数据经过FFT后，在频域同一频点只包含单个频域数据，利用单个频域数据求取协方差矩阵时，出现非满秩情况，致使MVDR方法无法实现对目标方位的有效估计.采用对角加载技术，可以在一定信噪比下提高协方差矩阵的稳定性，实现了对目标方位的有效估计.CCPMVDR方法在一帧数据内通过时域多个采样点的累积实现满秩协方差矩阵的稳定获取，相比DLMVDR方法而言，CCPMVDR方法对最低信噪比的要求降低了 2 dB.

当SNR=-15 dB时，由MVDR、DLMVDR和CCPMVDR方法通过200次独立统计所得不同信号长度下的目标方位估计均方误差如图2所示.其中：Ts为信号长度.

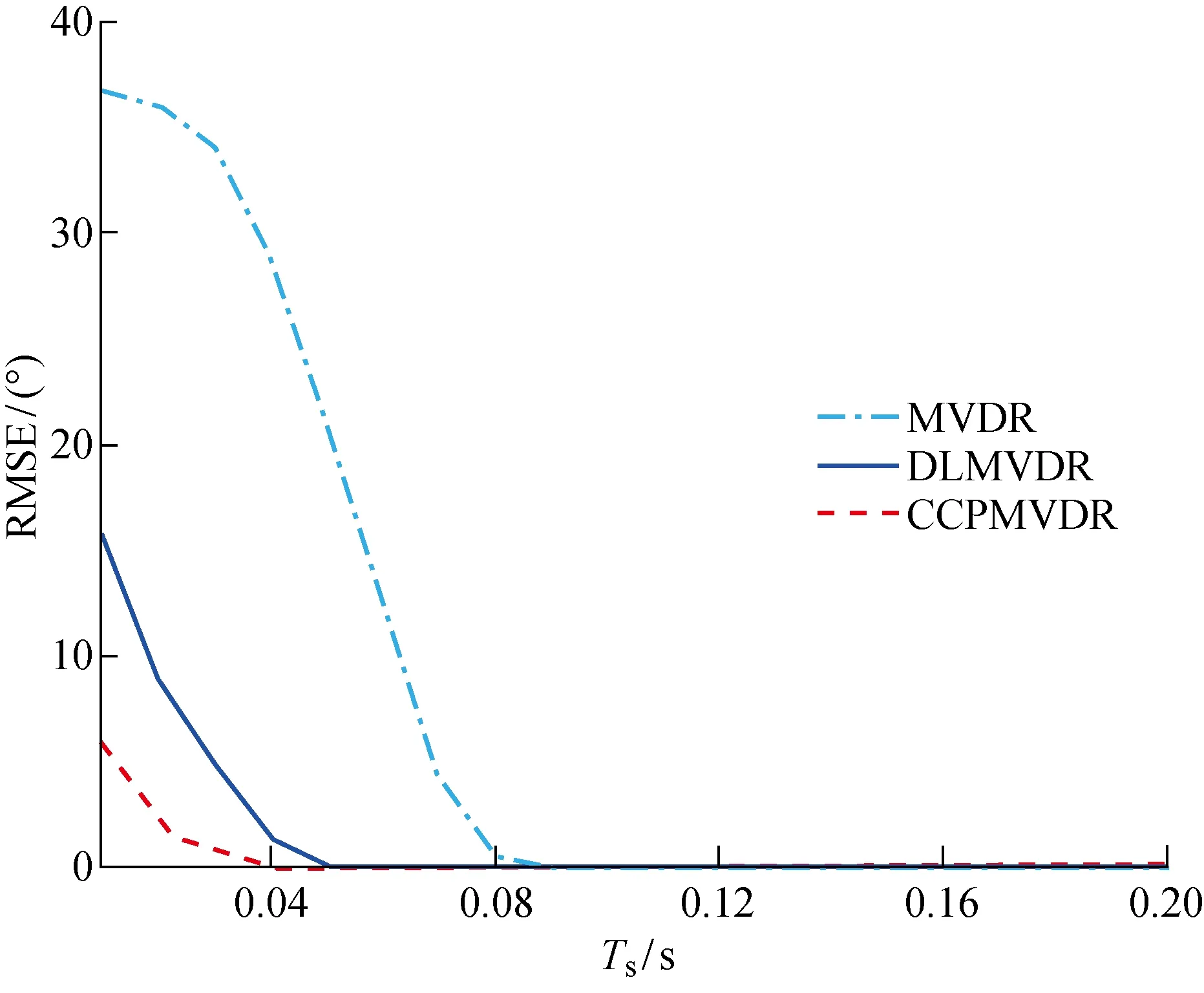
图2 不同信号长度下，3种方法的RMSE

该结果进一步验证了CCPMVDR方法对信号长度具有较好的宽容性.

3.1.2多目标情况 仿真条件：接收阵条件、系统采样率、一次采样长度、MVDR方法、DLMVDR方法和CCPMVDR方法处理过程与单目标情况一致.目标信号变为2个等强度的宽带信号，目标信号带宽均为 1 400～1 600 Hz，目标方位分别为90° 和100°，Ts=0.01 s.当SNR=-15 dB情况下，3种方法所得的空间谱如图3所示.其中：A为空间谱幅度.

图3 3种方法所得的空间谱(Ts=0.01 s)

由图3的仿真结果可知，相比MVDR方法和DLMVDR方法所得的空间谱，CCPMVDR方法可对相邻多目标方位实现有效估计，进一步验证了CCPMVDR方法可在短时间内获得良好的协方差矩阵估计和权向量最优解.

不同目标信号长度下，3种方法对空间谱的估计结果如图4所示.该结果进一步验证了一次处理数据中目标信号长度减小对CCPMVDR方法空间谱的估计性能影响较小，而对MVDR方法和DLMVDR方法空间谱的估计性能影响较大.

图4 不同信号长度下，3种方法所得的空间谱

由图4的仿真结果可知，相比于MVDR方法和DLMVDR方法，CCPMVDR方法降低了协方差矩阵估计对空间数据稳定性的要求，提升了空间谱估计的稳定性.

另外，相比于MVDR方法，CCPMVDR方法首先在子阵维度上进行相参累积处理，形成一次指数函数等列式求和运算，然后按空间重采样思想进行方位估计，该过程形成了两次指数函数等列式求和运算，平滑了背景噪声在非目标方向上的能量值，提升了空间谱主旁瓣能量比，该仿真结果也进一步验证了该分析结论.

3.1.3运算量分析 由于CCPMVDR方法在实现过程中可事先求取所需的复解析小波，然后再将其应用于后续方位估计中，所以影响CCPMVDR方法的运算量主要在于复解析小波函数与拾取数据卷积运算、协方差矩阵及其求逆运算，计算复杂度为

O{Θ[N(M+M2)+MN2+N4]}

其中：M为单帧数据长度.而DLMVDR方法在方位估计中需要将拾取数据变换到频域，然后在频域对每一个频点进行协方差矩阵求逆影响DLMVDR方法的运算量主要在于对拾取数据的FFT运算和每一个频点的协方差矩阵及其求逆运算，计算复杂度为

O{Θ[(2N-1)NfftlbNfft+NB(2N-1)2+

NB(2N-1)4]}

其中：Nfft≥M为FFT点数；NB为处理频带所含频率点数.

由上述分析可知，在阵元数一定时，DLMVDR方法的算法复杂度主要受处理频带影响，而CCPMVDR方法的算法复杂度主要受单帧数据长度影响，对于宽带信号处理，CCPMVDR方法在运算量上具有一定的优势.

为了直观地给出CCPMVDR方法的计算时间，在 3.1.1 仿真数据处理中，利用Intel(R)Core(TM)i7-7500U@2.7 GHz 2.9 GHz上运行的MATLAB2014b CPU TIME测出DLMVDR和CCPMVDR方法的运算时间，如表1所示.其中：t′为单帧运算时间.

表1 2种方法的运算时间

3.2 海试数据分析

为进一步验证CCPMVDR方法对实际试验数据空间谱的估计性能，分别利用MVDR方法、DLMVDR方法和CCPMVDR方法对接收阵海上试验数据进行处理分析，接收阵为32阵元等间隔水平阵，阵元间距为0.5 m，系统采样率为20 kHz.水平阵布放示意图如图 5所示.水深为100 m，海况3级，搭载平台与水平阵之间距离约为500 m，搭载平台航速为4 kn，搭载平台声级约为115 dB@1 kHz，环境噪声级约为72 dB@1 kHz.

图5 接收阵布放示意图

本次处理数据为平台返回基地过程所得，可视距离内存在多个目标，其中，相对接收阵方位50°、60°、85°、110°和130°为吨位较大船只，声级约为 120～130 dB@1 kHz.

MVDR方法估计协方差矩阵时，一次处理数据采用2×104个采样数据，3种方法处理数据过程与数值仿真过程一致.图 6～8为3种方法的输出时间历程，其中：t为处理数据对应的时刻.图9为3种方法的输出空间谱.

图6 MVDR方法输出方位历程

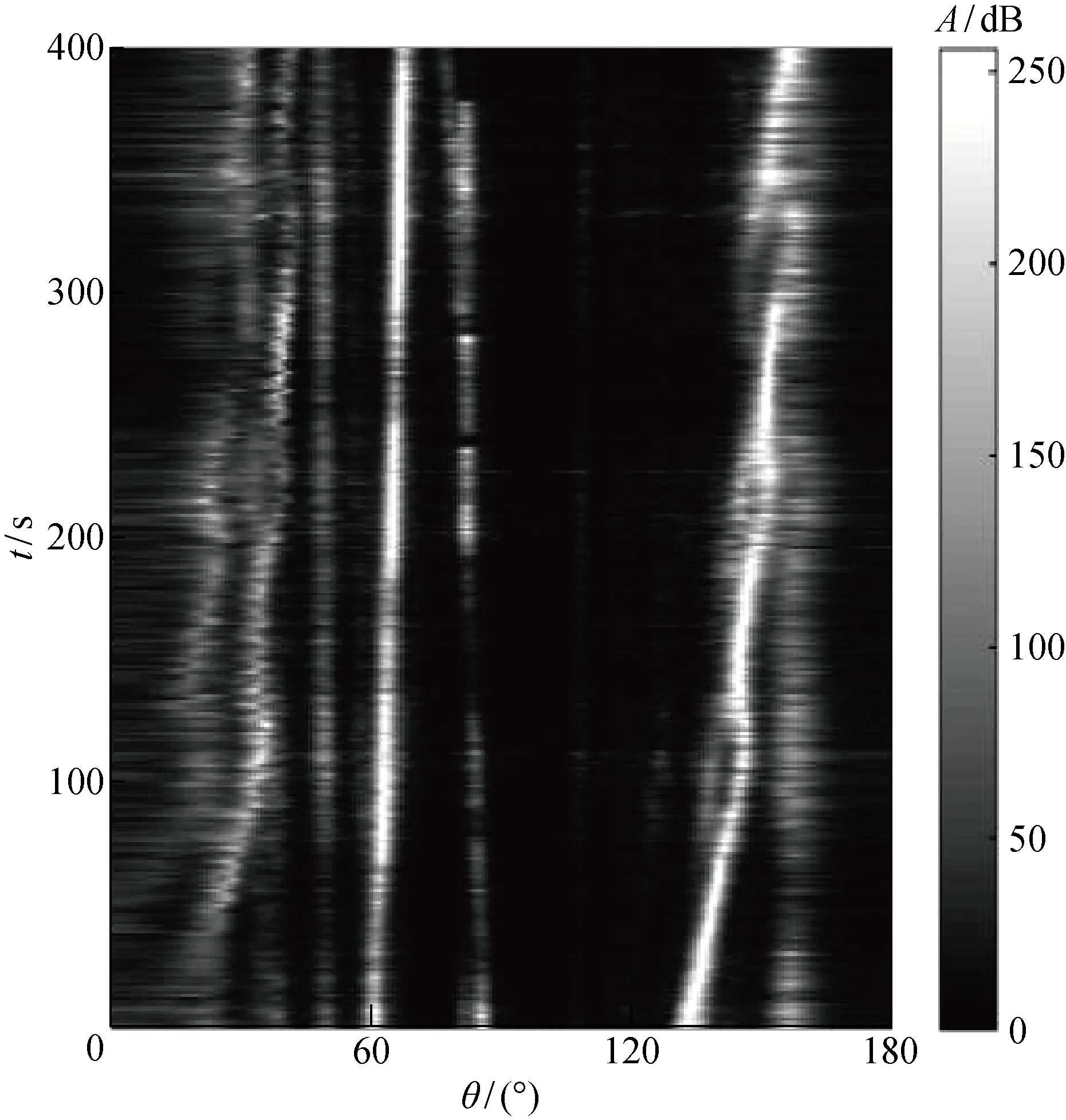
图7 DLMVDR方法输出方位历程

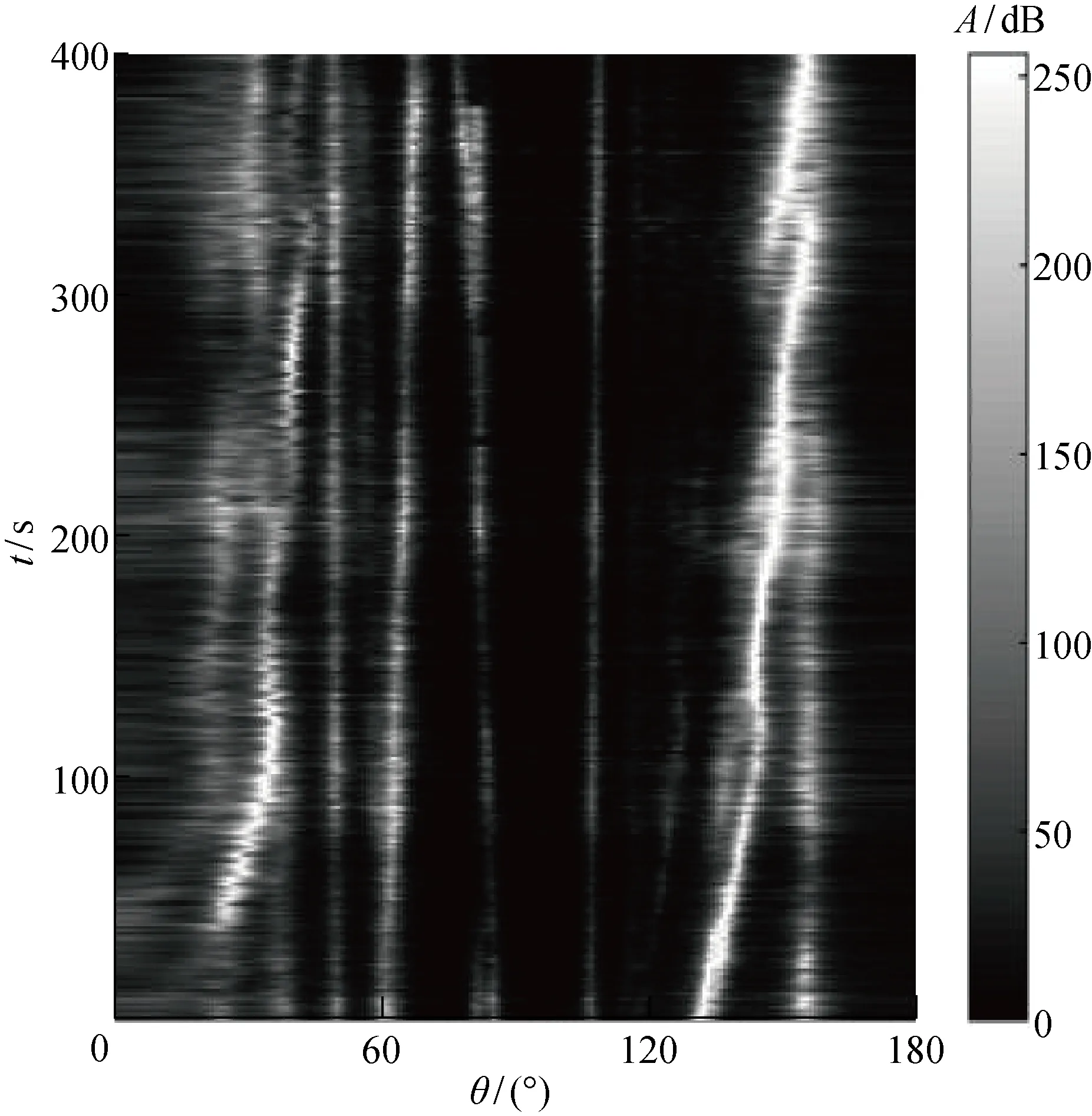
图8 CCPMVDR方法输出方位历程

图9 t=300 s时，3种方法所得的空间谱

由图6～9可知，MVDR方法所得空间谱在0～400 s时间段内无法对目标方位实现有效估计，而CCPMVDR方法所得空间谱形成的方位历程能清晰地显示50°、60°、85°、110°、130°和160°(搭载平台)目标航迹，目标方位明晰可辨.DLMVDR方法充分利用对角加载技术，提高了协方差矩阵的稳定性，可对该时段的多个目标方位实现有效估计，但对110°处目标方位估计效果劣于CCPMVDR方法，原因在于CCPMVDR方法在子阵维度上进行相参累积处理，相比DLMVDR方法多了一次指数函数等列式求和运算，有效平滑了背景噪声在非目标方向上的能量值，提升了110° 处目标方位主旁瓣能量比，进而提高了110°处目标方位的估计效果.

数据处理结果再次验证了CCPMVDR方法通过对接收阵拾取数据进行时域复解析变换和相参累积预处理，在短时间内实现了稳定获取权向量最优解，提高了空间谱估计的稳定性.

4 结语

针对最小方差无畸变响应空间谱估计方法稳定性问题，首先分析了影响最小方差无畸变响应方法的不稳定因素；然后针对影响因素，提出了CCPMVDR方法；最后给出了该方法的实现流程和性能分析.该方法通过时频分析处理，改变了构建协方差矩阵的数据来源，在短时间内获得了足够多的时间采样点数，在一帧数据内通过时域多个采样点累积实现了满秩协方差矩阵的稳定获取，降低了空间数据稳定性对最小方差无畸变响应方法产生的影响.同时，充分利用各阵元相位信息，在子阵维度上实现了数据相参累积，形成一次指数函数等列式求和运算，使协方差矩阵估计值中主对角线信号能量得到了有效增加，进一步降低了协方差矩阵估计对空间数据稳定性的要求.数值仿真和海试数据处理结果进一步验证了，相比于MVDR方法和DLMVDR方法，CCPMVDR方法通过改变协方差矩阵数据来源和两次指数函数等列式求和运算，提升了空间谱主旁瓣能量比，降低了协方差矩阵估计对空间数据稳定性和最低信噪比的要求，提升了空间谱估计的稳定性.