Welch谱估计的随机误差与置信度

朱学旺，刘青林，张思箭

（中国工程物理研究院总体工程研究所，四川 绵阳 621999）

振动环境工程研究中，通常采用Welch方法来获得随机振动信号的功率谱密度估计（Welch谱估计）[1—2]。Welch谱估计本质上是修正周期图方法的一种，其做法是通过对振动信号的分段平滑、数据重叠以及加窗处理等技术，以达到降低谱估计方差的目的。Welch谱估计是一致估计，即当用于谱估计的每段数据足够长且数据段足够多时，Welch谱估计结果的偏差和方差均等于0或趋于0[3—4]。令人遗憾的是，工程中用于谱估计的数据总是有限的，既不能保证每段数据足够长，也不能保证数据段足够多，即使对于平稳随机过程也是如此。为了便于操作，GJB 150.16A[5]和 MIL-STD-810F[6]对 Welch 谱估计给出了推荐要求：统计自由度不少于120，在试验频带内至少保证400线。换句话说，至少要60段数据，每段数据的长度要确保谱分析后的带宽小于5 Hz（当试验频率上限为2000 Hz时）。在这种状态（自由度取128）下获得的Welch谱估计，可以证明其随机误差与相同自由度χ2的随机误差相同（约为12.5%）。也就是说，该Welch谱估计的标准差与其均值（真值）的比为12.5%，但是其在一定置信概率下的置信区间并不知道。

为了提高welch估计的精度，加窗技术的研究一直受到相关研究人员的关注[7]。合理的窗函数，可以减小因为数据截断带来的能量泄露，继而减小谱估计的系统误差。谱估计的精度可以采用估计的偏差与估计的方差表示，小的方差表明单次估计接近真值的可能性大，是一种定性描述[3]。Welch谱估计的精度也可以定量描述，此时将谱估计结果作为一个随机变量的一次实现，可采用置信度分析方法获得其置信度与置信区间。文献[8—10]采用定量方法讨论了Welch谱估计的精度。针对不同的分布概率，其置信度分析的重点各异，文献[11]对置信度分析的现状进行了总结，而文献[12—13]对t分布变量的置信区间开展了专门研究。形式上，Welch谱估计可以表述为多个变量的平方和，与数学上定义的χ2分布变量具有类似的形式。一些经典的谱分析论著在讨论谱估计时也直接给出了与χ2分布变量相同的随机误差[3，14—15]，却没有进行详细的说明。文中给出了Welch谱估计随机误差的导出过程，试图证明其正确性。另外，为了进一步理解Welch谱估计随机误差的物理意义，研究了Welch谱估计结果的置信概率及对应的置信区间。通过正态标准化处理，能够将χ2变量的置信度分析方法应用于Welch谱估计结果的置信度分析。

1 χ2变量统计分析方法[14]

数学上定义的χ2（n）变量为n个独立的N（0，1）变量x1，x2，…，xn的平方和。即：

获得χ2（n）的均值m和方差σ2：

以均值和方差表述随机过程χ2（n）的随机误差为：

χ2（n）变量的概率分布p（Z=χ2（n））为：

置信概率与置信区间存在以下关系：

式中：a，b分别为置信区间的下限和上限，可查表得到I（a，n），I（b，n）后反推获得。自由度数较大的χ2（n）变量的分位数见表1，不同置信概率80%，95%，99%下的置信区间结果（利用了对称性假设）如图1所示[16]。

已知置信区间的上下限a，b时，可直接求得其对应的置信概率；反之，已知置信概率也可以导出对应的置信区间，只是此时需要假定上下限之外的概率分布。通常的做法是假定对称[16]，即小于置信区间下限的概率与大于置信区间上限的概率相等。

表1 χ2（n）分布的概率分布Table 1 Probability contribution of large D.O.F.χ2（n）variable

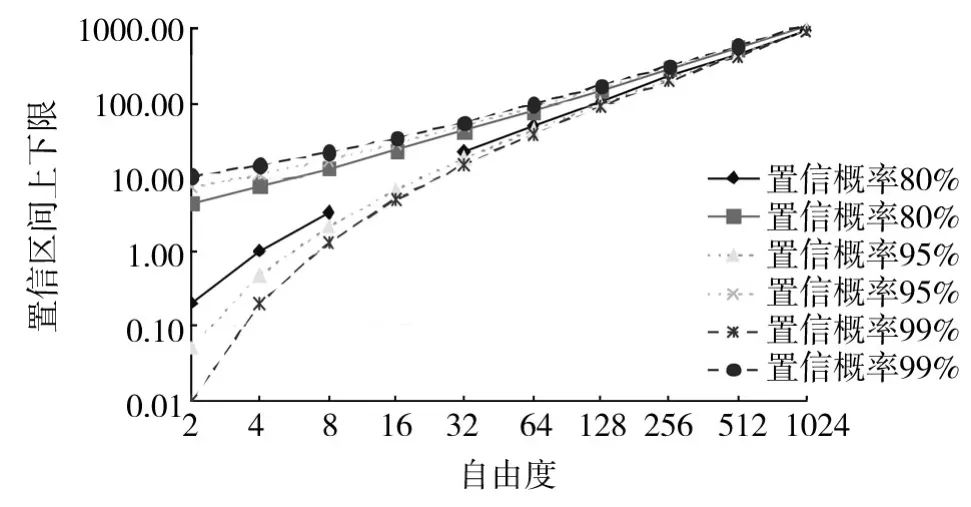
图1 χ2（n）变量的置信区间随统计自由度的变化Fig.1 Relationship between confidence interval and D.O.F.of χ2（n）variable

2 Welch谱估计的随机误差

为了导出Welch谱估计随机误差的表达式，首先回顾Welch谱估计方法。本质上，Welch谱估计是B-T估计的一种修正，其技术特点是加窗、分段平滑和重叠。具体过程是：将N个数据{x（0），x（1），…，x（N-1）}分为K段，每段数据长度为L，其中有L－D个数据为相邻段的重叠数据（D≤L），则：

第i段的L个数据为：

对每一段数据进行加窗处理，并分别计算其B-T周期图，有：

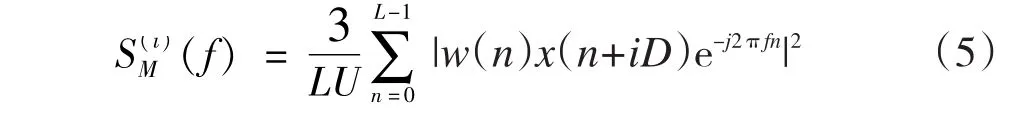
然后对各周期图进行平滑处理，获得N个数据的Welch谱估计：

由公式（5），（6）可知，Welch谱估计与原始信号（已经加窗处理）傅立叶变换的实部与虚部的平方和成正比。这样，公式（6）可改写为：

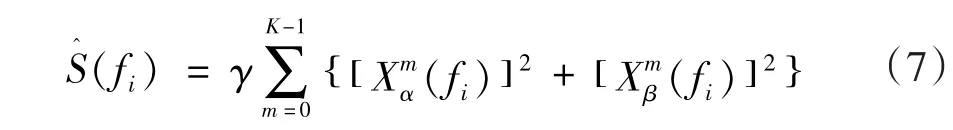
可以证明，当原始信号满足零均值正态分布时，其傅立叶变换的实部与虚部也满足零均值正态分布，且相互独立[15]，但是，不能保证其方差为1。为了能够利用第1节的结论，对傅立叶变换的实部与虚部进行正态标准化处理，此时，式（7）改写为：

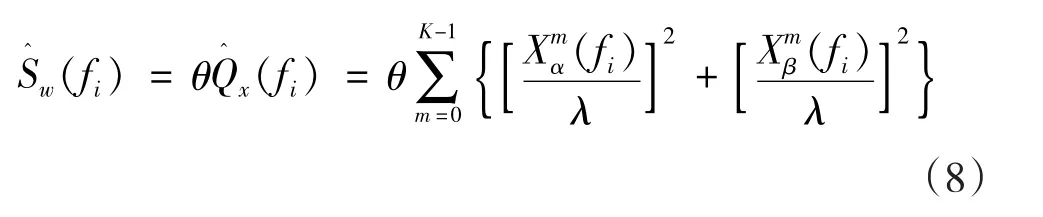
式中：θ=γλ2，λ为傅立叶变换的实部与虚部的标准差（假设其相同）。显然，

3 Welch谱估计的置信分析

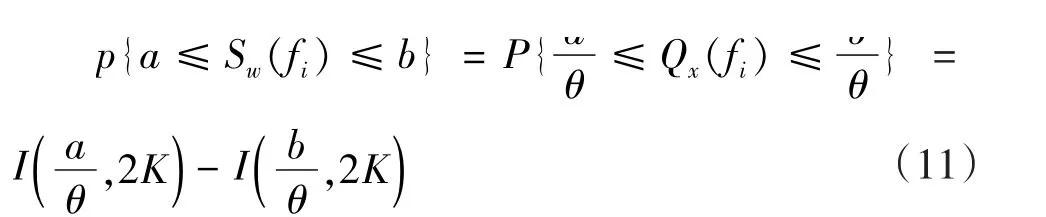
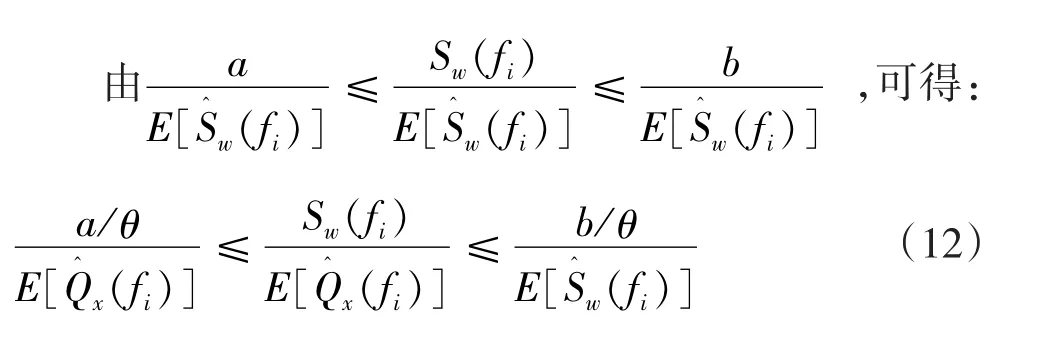
这样，便可以获得相应的置信概率。

4 算例及分析

算例一[14]：假定谱估计结果S0满足χ2分布，其分析自由度为10，则其在置信概率为80%的置信区间为（4.87，15.99），即：

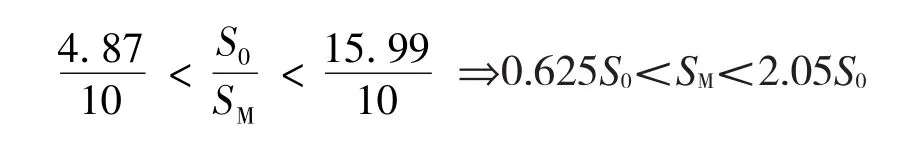
式中：SM为谱估计变量的统计均值。

相应地，99%的置信概率对应的置信区间为：0.397S0＜SM＜4.63S0。

算例二：假定S0的自由度为64，重复算例一的计算过程。其结果为：0.82S0＜SM＜1.28S0对应于置信概率80%；0.66S0＜SM＜1.66S0对应于置信概率99%。

算例三：假定S0的自由度为128，重复算例一的计算过程。其结果为：0.86S0＜SM＜1.19S0对应于置信概率80%；0.74S0＜SM＜1.41S0对应于置信概率99%。

从上述3个算例可以看出，随着自由度的增加，Welch谱估计的置信区间越来越趋向于均值集中。应用公式（12）可知，上述结果同样适用于工程中经常出现的高斯过程（均值为0，方差不等于1）的Welch谱估计。

GJB 150.16A和MIL-STD-810F都推荐谱估计的自由度要大于120，下面针对算例三进行专门分析。其结果表明，对应于置信概率80%，128自由度的Welch谱估计的均值在估计值的0.86～1.19倍之间，换句话说，估计值可能是均值的0.84～1.16倍；对应于置信概率99%，128自由度的Welch谱估计的均值在估计值的0.74～1.41倍之间，即估计值可能是均值的0.71～1.35倍。这一结果应该引起工程界的重视，因为获得的Welch谱估计可能比真实的谱高，也可能低。

128自由度的Welch谱估计的随机误差为12.5%，用此构造相对置信区间，则具有相同置信概率的χ2变量的置信区间为（87.5%×128，112.5%×128），对应的置信概率为68.4%。这是一个令人遗憾的结果，其表明128自由度的Welch谱估计结果仅有68.4%的置信概率能够实现其结果在真值的上下12.5%的范围内。

为了提高置信概率（依然以均值的上下波动12.5%作为相对置信区间），增加Welch谱估计的自由度，例如自由度取512，则其置信概率为95.5%。即有95.5%的可能，保证512自由度的Welch谱估计结果在均值的上下12.5%的范围内，此时，Welch谱估计的随机误差为6.25%。从这个意义上说，也许标准推荐的Welch谱估计的自由度120未必合适，尤其对于具有长数据的平稳随机振动的项目。

5 结论

1）Welch谱估计的随机误差与标准χ2变量的随机误差相同，仅与统计自由度有关。

2）基于χ2变量的置信分析方法可以应用于Welch谱估计的置信分析。

3）128自由度的Welch谱估计的随机误差为12.5%，以此作为谱估计的相对置信区间，其置信概率仅为68.4%，若要提高置信概率到95%，则Welch谱估计的自由度要512以上，此时的随机误差小于6.25%。

4）结论未考虑χ2变量概率密度函数的不对称性。

[1] 邓泽怀，刘波波，李彦良.常见的功率谱估计方法及其Matlab仿真[J].电子科技，2014，27（2）：50—52.DENG Ze-huai，LIU Bo-bo，LI Yan-liang.Common Power Spectrum Estimation Methods and Matlab Simulation[J].Electronic Sci＆ Tech，2014，27（2）：50—52.

[2] 姚武川，姚天任.经典谱估计方法的Matlab分析[J].华中理工大学学报，2000，28（4）：45—47；YAO Wu-chuan，YAO Tian-ren.Analyzing Classical Spectral Estimation by MATLAB[J].J Huazhong Univ of Sci&Tech，2000，Vol.28（4）：45—47

[3] 姚天任，江太辉.数字信号处理[M].武汉：华中科技大学出版社，2000.YAO Tian-ren，JIANG Tai-hui.Digital Signal Processing[M].Wuhan：Huazhong Univ of Sci&Tech Press，2000.

[4]LINDA S，MALENKA M，WOLFGANG M，et al.Optimized Spectral Estimation for Nonlinear Synchronizing Systems[J].Physical Review，2014，89（3）：032912.

[5]GJB 150.16A—2009，军用装备实验室环境试验方法第16部分振动试验[S].GJB 150.16A—2009，Military Equipment Laboratory Environmental Test Methods Part 16：Vibration Test[S].

[6]MIL-STD-810F，Environmental Engineering Considerations and Laboratory Tests，Method 514.5 vibration[S].

[7]TURGAY K，MELIH C I.The Obtaining of Window Function Having Useful Spectral Parameters by Helping of Genetic Algorithm[J].Procedia-Social and Behavioral Sciences，2013，83：563—568.

[8] ALEKSEEV V G."Welch-Type Estimator for a Spectral Density Function，the Case of Discrete-Time Parameter"，[J].Avtometriya，2001（6）：77—91.

[9]ALEKSEEV V G，SUKHODOEV V A.Welch-Type Spectral Density Estimator，Additional Recommendations[J].Optoelectronics，Instrumentation and Data Processing，2008，44（4）：302—305.

[10]ALEKSEEV V G，SUKHODOEV V A.Welch-Type Estimator for a Spectral Density Function，Case of a Continuous-time[J].Optoelectronics，Instrumentation and Data Processing，2009，45（2）：107—112.

[11]RICHARD K B，JORGE Q，HARIHARAN K I.The Present Status of Confidence Interval Estimation for One-factor Random Models[J].Journal of Statistical Planning and Inference，2006，136：4307—4325

[12]JOANNA T.Confidence Intervals for the Power of Student′s t-test[J].Statistics&Probability Letters，2005，73：125—130.

[13]DENNIS G，MINGFEI L.A Note on Confidence Intervals for the Power of T-test[J].Statistics&Probability Letters，2008，78：488—489.

[14]纽兰D E.随机振动与谱分析概论[M].北京：机械工业出版社，1980.NEWLAND D E.An Introduction to Random Vibration and Spectral Analysis[M].Beijing：China Machine Press，1980.

[15]戴诗亮.随机振动实验技术[M].北京：清华大学出版社，1984.DAI Shi-liang.Random Vibration Experiment Technique[M].Beijing：Tsinghua University Press，1984.

[16]蒋书法.最短置信区间的求解[J].上海电力学院学报，2014，30（2）：188—192.JIANG Shu-fa.Solution to the Shortest Confidence Interval[J].Journal of Shanghai University of Electric Power，2014，30（2）：188—192.

[17]吴昌昊，龚俊，刘子琪.基于CUDA实现经典功率谱估计[J].四川兵工学报，2013（10）：98—101.WU Chang-hao，GONG Jun，LIU Zi-qi.Achievement of Classic Power Spectrum Estimation Based on CUDA[J].Journal of Sichuan Ordnance，2013（10）：98—101.