考虑退化交互的多部件系统动态机会维护建模
2020-12-15于文莉周晓军
于文莉, 周晓军
(上海交通大学 工业工程与管理系,上海 200240)
状态维护的有效实施取决于对设备合理的状态评估与维护决策.随着制造系统的日益复杂,设备内部各关键部件性能退化的随机相关性问题日渐突出[1-2],部件退化进程的相互影响变得不可忽略,这意味着传统维护理论中对部件退化的独立性假设将不再适用.为此,如何将部件退化的随机相关性引入状态维护以更为准确地识别设备的性能状态和维护需求,是当前状态维护建模亟待解决的新问题.
目前,面向复杂系统部件随机相关性的研究大多围绕故障交互进行,已有学者分别针对部件故障率交互[3-4]、故障冲击损害交互[5]等问题提出相应的交互模型.但由于故障数据的收集对于系统的运行时长要求较高,基于故障交互理论的应用存在较大的限制.为此,有学者基于动态监测下的部件退化过程数据,通过分析退化状态与退化速率的影响关系以解构多部件之间的退化交互作用.Wang等[6]通过分析随机冲击对部件退化增量与退化速率的影响,构建了多部件随机交互协同退化过程模型.Bian等[7]基于连续监测下的传感信号构建多部件退化交互模型,并实现动态交互下的部件剩余寿命预测.Shen等[8]通过引入交互矩阵以刻画部件状态恶化对相关部件退化量或退化速率的冲击作用.然而,上述退化交互模型多假设部件随状态连续退化交互.实际上,由于复杂系统中存在的结构相关性,当某一部件的累计退化量高于特定的阈值水平时,其他部件的退化加速程度常会产生突变,比如常见的连杆轴承机构中,若轴承发生严重程度的磨损或形变,将导致传动连杆配合不良,使得振动异常且加速老化.显然,现有交互模型尚未考虑部件的不同状态对退化交互效应的影响严重程度.此外,上述研究均未涉及上层的维护建模问题,尚无法解析维护动作对交互型部件退化过程所产生的作用.
针对多部件退化交互系统的状态维护建模问题,Rasmekomen等[9]以部件退化交互损失函数与维护成本为目标建立多部件系统的多维预防更换阈值决策模型.杨志远等[10]在区分主要部件和辅助部件的基础上,提出了针对分类部件的退化交互型预防更换策略,并以单位时间维修费用最小为目标构建维修决策优化模型.现有的研究大多只考虑部件各自的维护阈值优化,而缺少对多部件系统维护活动的整体优化.目前,针对多部件交互系统的整体维护策略研究相对较少.Mercier等[11]提出了动态交互下两部件成组更换的阈值型预防维护策略,并基于Markov更新过程理论构建维护决策模型.Li等[12]基于双部件并联系统退化的随机相关性与成组更换的经济相关性,提出了Copula交互下的概率阈值型维护合并规则.Do等[13]通过引入各相关部件的机会维护阈值以合并维护作业,同时基于Monte Carlo仿真优化双部件的更换阈值.上述研究中仅考虑了双部件交互系统的成组更换,尚未能推广应用于两部件以上组成的系统维护,且更换阈值是基于长期规划得到的静态结果,忽略了各部件退化交互过程的动态特性以及由此导致的个性化维护需求.显然,针对由更多部件组成的交互系统,阈值型成组更换策略尚有欠缺,结合各个部件的状态进行短期动态规划更为合理.此外,以上研究仍基于连续交互型的退化机制,且假设部件修复如新,缺少对退化交互型部件的修复非新机制的综合考量.
本文面向多部件可修复系统,以退化状态作为影响退化速率突变的关键因素,构建多部件分级退化交互模型;基于交互系统整体状态,引入变周期检测机制;通过分析修复非新对交互部件短期失效风险的改善程度,提出成本节约型的机会维护动态决策指标;建立结合变周期检测与修复非新的多部件退化交互系统机会维护动态决策模型,以有效降低多部件退化交互型系统的单位时间总维护成本.
1 部件退化交互建模
考虑一台由m个关键部件组成的设备,Xi(t)表示部件i在t时刻的退化状态特征变量(以下简称退化量),i=1,2,…,m.当t=0时,Xi(0)=0,表示部件的初始状态全新,Xi(t)≥0,且随着时间逐渐增大.假设部件i经过时长u后的总退化增量为ΔXi(u),且该增量由两部分组成:一部分来自于自身的自然退化,另一部分来自于其他部件退化状态的交互影响,则部件i的退化模型可定义为
(1)
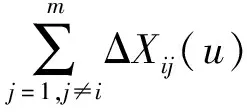
1.1 部件的独立退化增量
由于部件性能自然退化过程(如疲劳、磨损等)一般具有随机性且单调变化,而伽马过程能较好地表征此类特性,故假设部件的独立退化增量ΔXii(u)服从伽马分布Ga(x|αiiu,βi),其概率密度函数为
(2)

1.2 部件退化交互增量
部件的退化交互影响程度与部件之间的相互影响关系以及相关部件的性能退化状态密切相关.其中,部件之间的相互关系受到多方面因素的影响,如部件之间的结构连接关系(直接连接和间接连接等)、环境影响关系(受力关系和温度差别等).为此,引入退化交互因子δij以表征由此类复杂原因形成的综合退化交互影响关系.此外,考虑到部件的退化交互加速程度随着相关部件的性能退化而发生突变,且相关部件越接近失效阈值时产生的退化加速影响越大,为此将部件退化过程进行非等间隔划分,进而建立离散型退化交互模型.
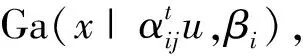
(3)

Sj(t)=S(Xj(t))=
(4)
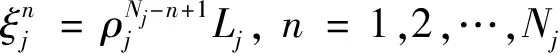


(5)
由以上定义可知,考虑交互的多部件退化模型将有别于传统的独立退化过程,部件状态退化所导致的退化速率跃变不可忽略.以两部件的退化交互系统为例,比较部件独立与交互时的退化曲线,如图1所示.其中:Tk为第k次检测时间;τk+1为这一次与下一次的检测间隔时间.由图1可知,由于受到部件1状态退化的影响,部件2的退化速率相对于独立时明显加速,达到失效维护阈值的时间也更短.因此,退化交互状态下的部件需要更为及时的预防维护.
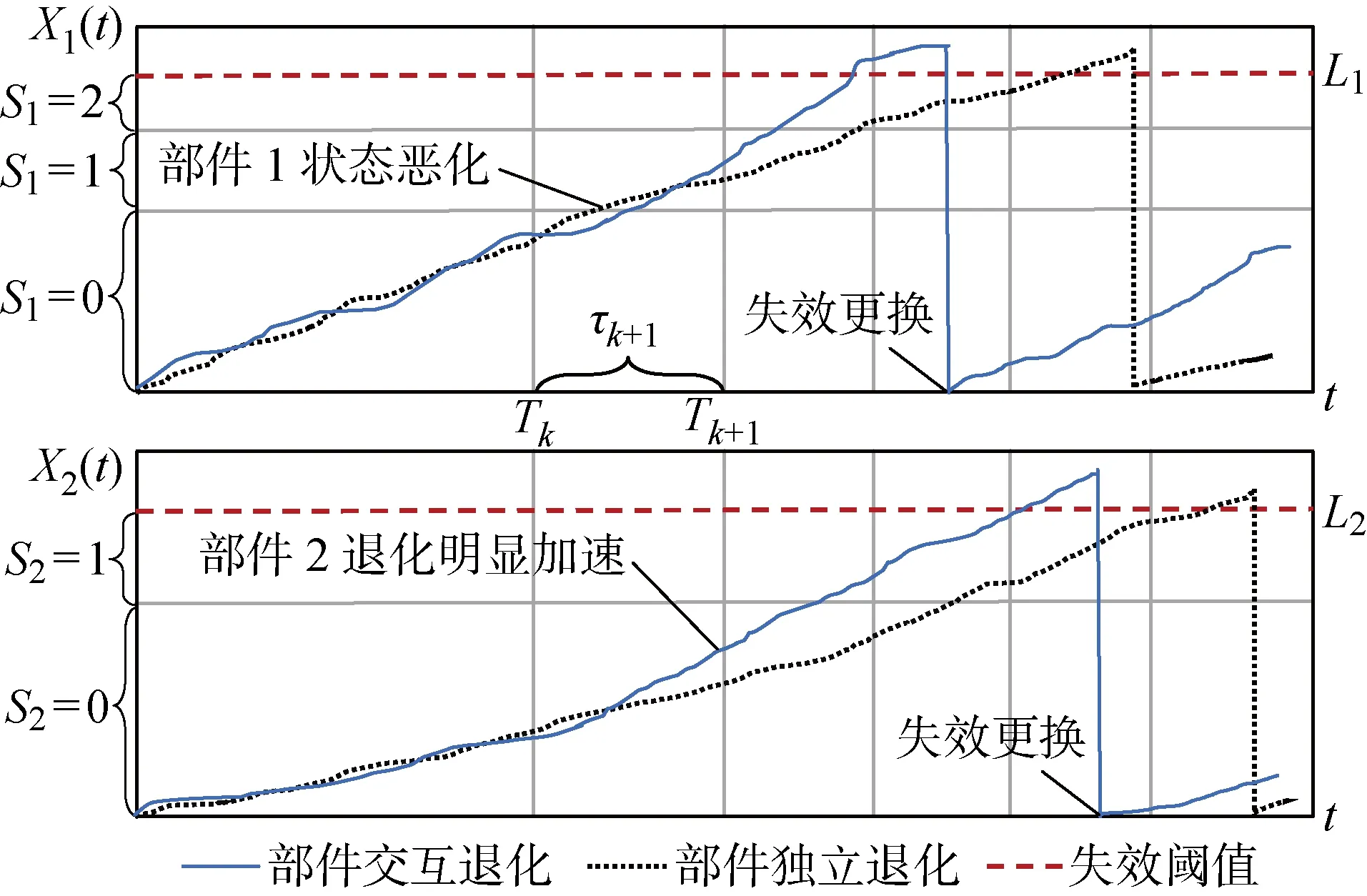
图1 两部件的退化交互过程示意图
2 维护建模
2.1 基本假设与设定
假设到达既定检测时间时,对m个部件同时进行检测,检测值为部件状态真实值,检测用时忽略不计,检测后立即进行维护动作.仅考虑部件的退化失效,且失效需通过检测判定.

(6)
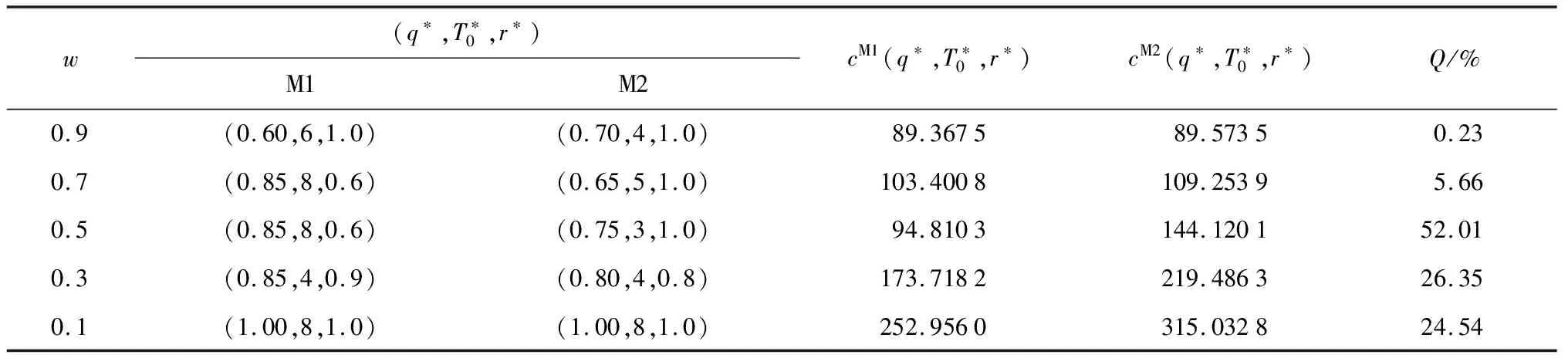
式中:q(0 基于上述假设,在给定的检测策略与预防维护阈值下,将每次停机维护看作一个机会维护决策阶段,通过比较不同部件组合下的机会维护方案带来的短期效益,动态获取该阶段机会维护的部件集合,进而对各阶段维护成本进行累加以获得规划时间区间内的总维护成本.在此基础上,通过最小化单位时间总维护成本获取优化的检测策略与预防维护阈值.在以上决策过程中,还需完成3方面的建模工作:变周期检测建模、机会维护动态决策建模以及规划区间优化目标建模,即总维护成本率的建模. 在业已构建的退化交互模型下,相关部件的状态等级越高,其退化交互速率越大.为此,在部件越接近失效阈值时安排更为频繁的检测可有效地规避失效风险.基于这一考虑,结合Barker等[14]提出的检测间隔时间函数,本文将在交互系统整体退化状态等级划分的基础上建立变周期检测模型.第k+1次检测时间定义为 (7) 式中:T0(T0≥1)为设备良好时的基准检测间隔时间;r(0 考虑到退化交互,部件的维护将产生两方面的影响:一是直接降低部件的退化量水平;二是通过降低部件退化状态等级从而间接降低对相关部件的退化加速影响.因此,设备停机维护时,部件的机会维护能延缓退化交互的加速效应,进一步提高系统可靠性,但同时增加了机会维护成本. 为了进一步衡量不同部件组合机会维护所带来的短期效益,引入失效风险节余成本.由已构建的退化交互模型和变周期检测模型可知,不同部件组合机会维护前后的状态变化将影响系统的下一次检测间隔时间以及各退化交互部件在下一次检测前发生失效的风险水平.为此,计算所有部件阶段机会维护的短期收益应包括机会维护前后各部件产生的所有失效风险节余成本.在此基础上,将所增加的机会维护成本作为该阶段额外增加的短期成本,进而以短期收益与短期成本之差构建动态机会维护指标,获取部件机会维护组合.具体建模过程如下. (1)确定维护后各部件的退化状态.不同的维护决策与维护动作决定了部件的退化状态,考虑维护决策部件i的退化量为 (8) (9) (10) (2)规划下一次检测间隔时间.根据维护后的部件退化量取值,更新部件状态等级,并以θ=[θ1θ2…θm]表示系统各部件维护状态向量,则下一次检测间隔时间为 τk+1(θ)=τk+1([θ1θ2…θm])= (11) (12) 在此基础上,部件i在下一次检测时(t=Tk+1)达到失效阈值的风险概率可表示为 (13) (14) Ik(θ)=Ik(θ1,θ2,…,θm)= (15) (16) 结合检测总次数K可以求得维护规划区间内的总成本为 (17) 考虑一台由3个关键部件组成的设备,部件的退化速率水平分别为低、中、高,退化交互矩阵为 表1 各部件参数设置 6种不同的(T0,r)取值组合下总成本率随q值的变化曲线如图2所示.由图2可知,对于不同的取值组合(T0,r),均存在最优的系统预防维护阈值比例因子q使得总成本率最低,进而验证了迭代法对于求解本算例的可行性.从整体来看,基准检测间隔时间T0(或检测间隔调整因子r)越小,最优q值取值越大.这是由于部件的频繁检测可更为及时地获取部件退化量,从而保障部件在退化水平较高时才进行预防维护,以更充分地利用部件的剩余使用寿命.而在相同T0下,非等间隔检测策略(r<1)的总成本率优于等间隔检测策略(r=1),这是因为检测间隔调整因子r越小,部件状态退化时检测越频繁,进而更为有效地防止部件失效,从而降低总成本率.此外,当r值相同时,T0越小,最优成本上升,此时是因为部件状态良好时检测频繁,从而导致检测成本增加,使得总成本率偏高. 图2 不同(T0,r)组合下,q与c(q,T0,r)的关系 图3 不同(T0,r)下的c(q*,T0,r)关系(q*=0.86) 表2 不同(T0,r)下的与最优的GAP对比(q*=0.86) 为了进一步验证模型的合理性,将各部件的失效更换成本取值调整为部件的预防维护成本的不同倍数,进而分析不同的成本比值对维护决策结果的影响.不同成本比值下的维护决策结果如表3所示.从表3的仿真优化结果可知,当部件的失效更换成本接近预防维护成本时,预防维护阈值取值较高且系统检测周期较长,说明在较小的成本比值下,系统无需过多的预防维护;而随着成本比值增大,预防维护阈值降低且变周期检测变得频繁,说明在较高的失效成本下,应加大对系统的监控力度与预防维护力度,以尽量规避失效带来的巨大经济损失. 表3 不同成本比值下的维护决策结果 为验证所构建的基于退化交互的机会维护动态决策模型的优越性,从两方面进行对比分析:一是验证维护决策时考虑退化交互作用的必要性;二是通过对比无机会维护的预防维护模型结果,体现本维护模型对于退化交互可修复系统的维护成本优势. 3.2.1退化交互考虑与否的对比分析 基于决策者忽视部件相关关系的情形(即δ=0),按照所建维护模型求得使总成本率最低的最优决策参数,作为不考虑退化交互时的决策结果,并以此维护决策结果用于算例中的3部件退化交互系统,求得该组决策参数下的总成本率,最后与考虑退化交互下的算例结果进行对比.在保持其他参数设置一致的情况下,优化结果如表4所示. 由表4可知,在忽视部件退化交互的情形下,多部件系统采用了间隔相对较短的等周期检测方式,且预防维护阈值较低,其总成本率比考虑部件退化交互下的优化结果高出19.69%,说明对于实际中存在退化交互的多部件系统,忽略部件的退化相关性而做出的维护决策,将导致维护成本偏高. 表4 不同部件相关关系考虑下的维护决策结果对比 不同修复程度下的模型对比结果如表5所示,其中:Q为成本增幅.由表5可知,无论w如何取值,动态机会维护都能有效降低维护总成本率,尤其在修复程度较低的情况(如w=0.3,0.5)下,动态机会维护具有显著的成本优势.当w=0.1时,两种模型下的最优决策参数一致,此时机会维护下的总成本率仍比较低,这是由于部件发生失效更换时,其他部件进行机会维护能降低退化交互加速影响,从而降低失效风险,减少失效维护成本. 表5 不同w下的模型结果对比 本文针对多部件系统中部件退化状态影响退化速率的动态特点,基于状态分级交互思想,构建多部件退化交互模型.在此基础上,引入考虑系统整体状态的变周期检测机制,建立成本节约型的多部件退化交互可修复系统机会维护动态决策模型.3部件退化交互系统的算例分析表明,维护决策时忽视部件退化相关性将导致系统的维护成本偏高.同时,不同修复程度下的模型结果表明,与不考虑机会维护的阈值型预防维护模型相比,机会维护动态决策模型在多部件交互系统的维护决策中具有成本优势.
2.2 变周期检测建模

2.3 机会维护动态决策建模
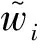

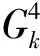



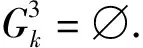
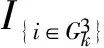

2.4 维护优化目标建模

3 算例分析
3.1 算例描述与结果分析
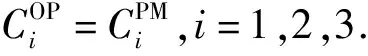

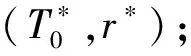



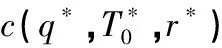

3.2 维护模型对比分析


4 结语
