高中数学教学中“启发设疑”的几点要求———正弦定理的教学感悟

◇ 山东 杨大伟

(作者单位:山东省淄博市高青县第一中学)

数学中涉及众多的公式、性质、定理,这些内容如果仅让学生强行记忆,很容易造成遗忘或混淆.反之,若通过教师的启发设疑,让学生自己去发现,并进行证明,就会使学生产生深刻的印象.本文以正弦定理的教学为例,说明“启发设疑”教学方式的应用.

案例正弦定理:在△ABC 中,a,b,c 分别为角A,B,C 的对边(其中2R为三角形外接圆直径).

1 要立足学生的最近发展区

教师:在直角△ABC 中,角C 为直角,由三角函数的定义,得

观察一下这三个式子的结构,有什么特征?

生1:a 和A,b 和B,c 和C 成对出现,且这三个式子中都含有c.

教师:能不能据此建立三个式子之间的关联?

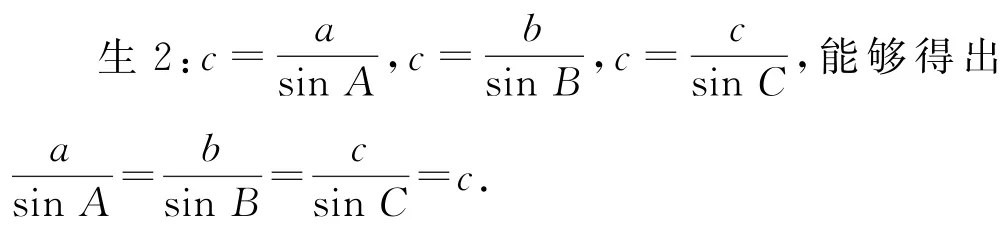
直角三角形是特殊的平面几何图形,探究三角形有关性质、定理,可从直角三角形入手.

2 要承上启下、循序渐进

教师:如果把直角三角形换成一个普通的钝角或锐角三角形呢?

生3:如图1所示,作BC 边上的高AD,在直角△ABD 中有在直角△ADC 中,有所 以csinB ＝bsinC,进而可得同理,得在钝角三角形中也存在这一关系.

图1

数学中很多重要的性质、定理都是由特殊到一般的推理得到的,对于正弦定理的教学,由直角三角形,可顺理成章地推广到斜三角形中.

3 要善于激发学生的探究热情

生4:c 是直角三角形的斜边,也是三角形外接圆的直径,那有可能等于三角形外接圆的直径.

教师:有了大胆的假设,就进行大胆的证明.

生4:如图2,作出△ABC的外接圆O,过点B 作直径BD.根据圆的几何性质可知在Rt△ABD 中即

图2

随着教师设问的引导,学生探究不断深入,探究热情被有效地激发出来,都想尽快发现这一新大陆.

4 要让学生明确探究的价值

上述探究过程,提供了一种解题的方法,即与三角形有关的问题,往往可通过构造其外接圆进行求解.

练习在△ABC 中,a,b,c 分别为角A,B,C 所对的边,若a＝2,A＝60°,求△ABC 面积的最大值.

构造三角形的外接圆,在圆中弦BC 为定值,其所对的圆周角为角A(定角),过点A 作AD ⊥BC 于点D,则三角形的面积等于当AD 最大时,三角形的面积最大,即△ABC 为等腰三角形.

将探究方式应用于解题,使学生明白“过程决定方法”的真谛,明确探究价值所在.

总之,数学学习就是提出、分析、解决问题的过程,恰当、巧妙的设问方式是引导学生学习新知识、探究新规律、发现新结论的有效形式.