探求规律,破解数列新颖题
2020-12-14山东崔洪涛
◇ 山东 崔洪涛
(作者单位:山东省滕州市第一中学)
虽然高中阶段我们只重点学习了等差数列和等比数列,但在高考中由它们派生出来的数列新颖题却层出不穷.面对这类问题,我们该怎么求解呢? 本文进行举例说明.
1 从图形的变化中探求规律
有时数列是由图象给出的,而图象的变化过程蕴含了数列的通项,我们可以通过对图形变化趋势的分析得到数列通项形式.
例1如图1所示,线段AB 的长度为a,在线段AB 上取两个点C,D,使得以CD为一边在线段AB 的上方作一个正六边形,然后去掉线段CD,得到图2中的图形;对图2中的最上方的线段EF 进行相同的操作,得到图3 中的图形.依此类推,就可以得到一系列图形.把第n 个图形的所有线段的长度加起来,它的和记为Sn(注:图1视为第1个图形),这里给出关于数列{Sn}的4个命题:
① {Sn}为等比数列;
② {Sn}单调递增;
③ 一定存在最小正数a,使得对一切正整数n,Sn>2019都成立;
④ 一定存在最大正数a,使得对一切正整数n,Sn<2019都成立.
其中真命题的序号是________(请写出所有真命题的序号).
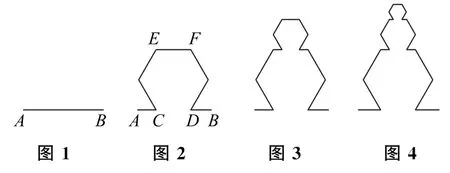
根据题意,S1=a.图2中的正六边形的边长是于是图3中那个最小的正六边形的边长是所以
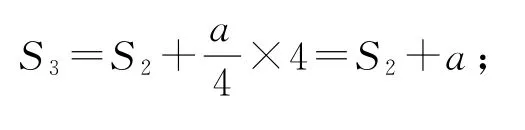
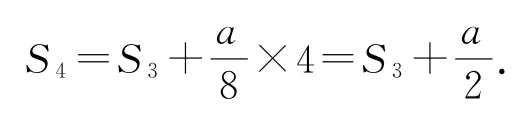
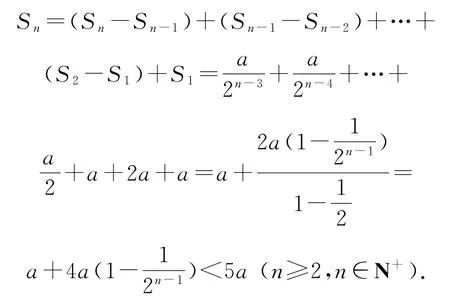
又S1=a<5a,所以存在最大的正数使得对任意的正整数n,都有Sn<2019,即③错误,④正确.故答案为②④.
本题要求我们能根据图形的变化规律求解通项公式,并会用累加求和的方法.解答时可根据题意先找出前几个图形间的关系,再推导出第n 个图形与第n-1个图形间的关系,从而得出递推公式进行求解.
2 从数列的递推式中探求规律
在现行课本中,对等差数列和等比数列的有关性质研究较多,也比较透.有些数列虽然不是“纯粹”的等差数列或等比数列,但通过探究规律、合理转化,发现也可以利用等差数列或等比数列的知识与方法加以解决.
例2已知从2开始的连续偶数蛇形排列形成宝塔形数表,第1行为2,第2行为4,6,第3行为12,10,8,第4行为14,16,18,20.如图5,在宝塔形数表中位于第i 行、第j 列的数记为ai,j,比如a3,2=10,a4,2=16,a5,4=24,若ai,j=2020,则i+j=( ).
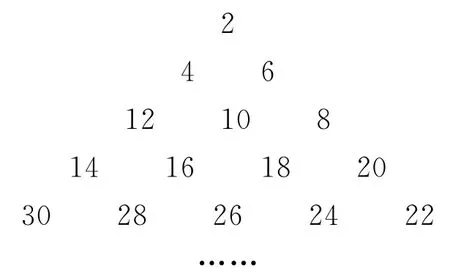
图5
A.65 B.70 C.71 D.72
由图5可知,第1行放1个偶数,第2行放2个偶数,第3行放3个偶数……又因为ai,j=2020指图中摆放的第i 行第j 列,所以先求第m 行的最后一个偶数,该偶数小于2020且是最接近的,并且还能成为每一行的最后一个数字则m≤44,当m≤44时,44(1+44)=1980,则第44行的最后一偶数是1980,第45行的第45个偶数为1982,利用等差数列的任意两项之间关系可知2020应处于该行的第45-19=26列,故j=26,所以i+j=45+26=71.故选C.
根据题意知正偶数an构成一个等差数列,研究图形可以发现,图中每一行排列的数、每一行的数字总数与本数列的每一项的关系都是有规律可循的,这就是我们解题的切入口.
3 从等差与等比的类比中探求规律
类比是解数学问题的有效途径,解题时通过类比等差数列与等比数列的性质,往往会有新发现.
例3已知真命题A:在等差数列{an}中,若m,n,p,q∈N,且m+n=p+q,则am+an=ap+aq;真命题B:在等比数列{an}中,若m,n,p,q∈N,且m+n=p+q,则am·an=ap·aq.我们称这两个真命题具有“加↔乘”类比关系.请在等差数列和等比数列的范围内,分别写一个具有“加↔乘”类比关系的命题,而且它们必须是真命题.
等差数列和等比数列中一般的类比规律如表1所示.
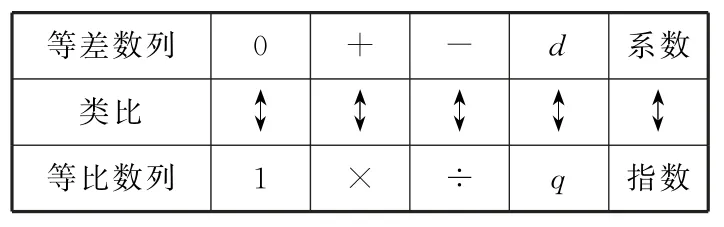
表1
于是我们可写出如下两个真命题.
真命题A:设a<b,在a,b 之间插入n 个实数x1,x2,…,xn,使这n +2 个数成等差数列,则有成立.
真命题B:若0<a<b,在a,b 之间插入n 个正数y1,y2,…,yn,使这n+2 个数成等比数列,则有成立.
类比是一种创新思维,是高考中经常出现的一种数学思想.
从以上三类问题可以看出,从表面上看是在考查数列知识,其实是在考查考生的创新思维,所以这类问题具有一定的难度,应引起大家的注意.
