通过一道习题及变式谈对函数的理解

◇ 安徽 李 华

(作者单位:安徽省颍上第一中学)

学习函数,关键是要抓住函数的三要素:定义域、对应法则与值域.那么函数的定义域、对应法则与值域三者之间有什么关系呢? 这个问题是教师教学首先要解决的问题.由于函数概念比较抽象,学生对函数概念的理解往往不到位,为此教师除了在理论上加以阐述外,还要从实例出发,让学生通过例子以及对例子延展来加深对函数概念的理解.例子从何而来,笔者认为应尽可能从教材中找,从教材例子出发,加以适当变式,以促使学生对函数概念形成完整认识.

引例探究是否存在函数f(x),g(x)满足条件:

(1)定义域相同,值域相同,但对应关系不同;

(2)值域相同,对应关系相同,但定义域不同.

本题要求同学们深刻领会函数的概念.我们必须明确,定义域、对应法则与值域,是函数的三要素,缺一不可.设函数的定义域为集合A,对应法则为f,则函数的值域为{f(x)|x∈A}.于是我们可以看出,函数的值域归根到底是由它的定义域和对应法则确定的.所以我们可以这样认为,如果两个函数的定义域和对应法则分别相同,那么这两个函数是同一个函数.

(1)如果存在函数f(x),g(x)满足条件:定义域相同,值域相同,但对应关系不同,那么这两个函数一定不是同一个函数.这样的函数是存在的,如下两个函数的定义域和值域都是[0,＋∞):f(x)＝x2,g(x)＝|x|.

(2)如果存在函数f(x),g(x)满足条件:值域相同,对应关系相同,但定义域不同,那么这两个函数一定也不是同一个函数.这样的函数同样是存在的,如函数f(x)＝x2,定义域为{0,1,2},则值域为{0,1,4};函数f(x)＝x2,定义域为{0,－1,－2},则值域也为{0,1,4}.

函数虽然体现了两个非空数集之间的对应关系,但归根到底函数是由定义域和对应法则确定的,因此我们在求函数关系式时,不要忘记注明函数的定义域.

变式1下列说法错误的是( ).

A.在函数值域中的每一个值都能找到与之对应的定义域中的值

B.函数的定义域是无限集,则值域也是无限集

C.当一个函数的定义域与对应关系确定后,它的值域也就确定了

D.若函数的定义域中仅有一个元素,那么它的值域中也仅有一个元素

本变式设计的目的是要求学生不仅要从正面理解函数概念,还要从反面的角度加以辨析,从而达到举一反三、融会贯通的教学效果.

变式2设M ＝{x|0≤x≤2},N ＝{y|0≤y≤2},图1的4个图象中,其中能表示由集合M 到集合N 的函数关系的有( )个.

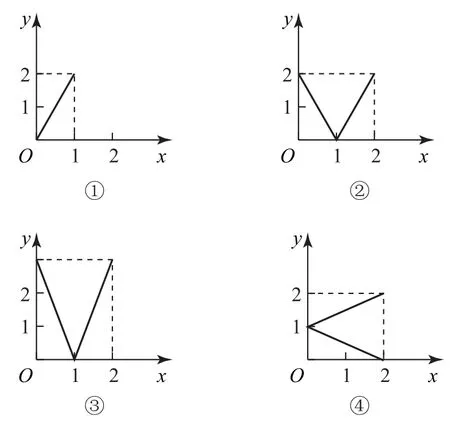
图1

A.0 B.1 C.2 D.3

①错,x＝2时,在N 中没有元素与它对应,故不满足任意性.②对,这种对应关系同时满足任意性与唯一性.③错,x＝2时,对应元素y＝3∉N,不满足任意性.④错,x＝1时,N 中有2个元素与之对应,不满足唯一性.故仅有②正确,选B.

本变式是变式1的特殊化,让学生从数与形的角度去进一步认识函数,领悟函数概念的内涵,即A 中元素无剩余,B 中元素允许有剩余.允许出现“多对一”,但不允许出现“一对多”.

变式3下列函数中,与函数y＝x＋1是相等函数的是( ).

判断两个函数是否相同,也是函数概念教学中的一个重点问题,看两个函数是否是同一个函数,不仅要考查函数的对应法则,还要考查函数的定义域.这两点往往容易被学生忽视,尤其是函数的定义域,本变式的设计目的就是要让学生感知函数概念中定义域的重要性.

变式4已知某函数满足如下两个条件:一是解析式为y＝x2,二是值域为{1,4},试问这样的函数有多少个?

当函数的解析式和值域确定后,它的定义域不是唯一的.本题可采用列举法,由已知的对应法则与值域,可得定义域可能是{1,2},{－1,2},{1,－2},{－1,－2},{1,－2,2},{－1,－2,2},{－1,1,2},{－1,1,－2},{－1,1,－2,2}.所以满足条件的函数有9个.

本变式是在前3个变式基础上的拓展,对学生有一定的能力要求.通过本题的解决,不仅可以让学生深刻领悟函数的概念,而且可以让他们的数学思维上升到一个更高的层次.

基于以上的分析,对于函数概念不难得出如下结论:

1)判断两个函数为同一函数的依据,一是定义域要相同,二是对应关系也要相同;

2)函数的定义域是函数的灵魂,它决定了函数的值域,并且它是研究函数性质和图象的基础,因此,我们一定要树立函数定义域优先意识.