高中数学函数与方程综合问题探究

◇ 安徽 应 莉

(作者单位:安徽省阜南一中)

函数与方程是高中数学的重要知识点,尤其是一些题型常将两者结合起来,难度较大.为提高学生解答该类问题的能力,教学中应注重做好相关习题的汇总,与学生一起探究解题思路,使其遇到类似问题时能快速解答.

1 运用图形,简化解题

可将有关函数零点的问题转化为方程问题,运用数形结合法求解,大大简化解题步骤,提高解题效率.教学中注重优选、讲解经典例题,使学生掌握运用数形结合法解答函数与方程综合问题的具体步骤.同时,鼓励学生进行课堂反思,把握解题的关键,在解题中少走弯路,尽快得出正确结果.

例1已知函数g(x)＝f(x)＋x＋a,若g(x)存在2个零点,则a 的取值范围为( ).

A.[－1,0) B.[0,＋∞)

C.[－1,＋∞) D.[1,＋∞)

图1

这是一道高考题,求解时,可对已知条件进行转化,再应用数形结合思想进行分析.g(x)存在2个零点等价于f(x)＝－x－a 存在2 个不等实根.在同一直角坐标系中分别绘制f(x)和y＝－x－a 的图象,如图1,因为y＝－x－a图象的斜率为－1,而－a 表示在y 轴上的截距,因此,要想满足题意,只需－a≤1,即a≥－1,故选C.

2 深挖条件,巧妙突破

解答函数与方程的综合问题时需认真审题,充分挖掘题干中的隐含条件,实现快速破题.教学中可结合学生的所学知识,注重在知识的交会处设计问题,并给学生专门留下独立思考的时间,鼓励其积极回顾所学知识,深挖已知条件进行问题求解,在巩固所学知识的同时,使其更好地掌握函数与方程综合问题的解题技巧.

例2若a,b 为函数f(x)＝x2－px＋q (p＞0,q＞0)的2个不同零点,且a,b,－2这3个数可适当排序后成等差数列,也可适当排序后成等比数列,则p＋q 的值为( ).

A.6 B.7 C.8 D.9

解答该题需要充分理解零点的含义,并根据数列知识求出p＋q 的值.很多学生面对该题时,会因无法巧妙应用题干中“等比数列”“等差数列”的相关知识,而无从下手.事实上,因为a,b 为方程x2－px＋q＝0的两个不等实根,由根与系数间的关系得a＋b＝p,ab＝q,又因为p＞0,q＞0,则a＞0,b＞0.若a,b,－2排序后为等比数列,则－2必为第二项,该等比数列为a,－2,b 或者b,－2,a,因此,必有ab＝4;若a,b,－2适当排序后为等差数列,则a－2＝2b 或b－2＝2a,解得a＝4,b＝1或a＝1,b＝4,则p＝5,q＝4,则p＋q 的值为9,故选D.

3 等价转化,巧用性质

解答高中数学函数与方程综合问题时应注重运用等价转化思想、巧用函数的相关性质.教学中为使学生掌握等价转化的方法,教师应注重选择代表性较强的习题,组织学生开展训练活动,使学生在训练中发现并弥补知识的漏洞,积累相关的解题经验.

例3已知方程x＝a(a 为常数)在区间[0,2π]上恰有三个根x1,x2,x3,则x1＋x2＋x3的值为( ).

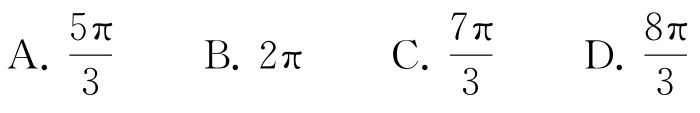
方程中涉及三角函数,一般情况下根无法直接求解.解题时可将其转化为函数问题,借助函数图象分析.因为令根据三角函数性质易得函数f(x)在上单调递增,在上单调递减,要想满足题意则需得出x＝1故选C.

总之,高中数学教学中为提高学生解答函数与方程综合问题的能力,促进学生数学成绩的提升,教师应注重讲解例题,积极组织学生开展专题训练活动,使学生掌握相关的解题技巧.