函数综合应用三要求

◇ 湖北 徐 涛

(作者单位:湖北省谷城县第一高级中学)

函数的综合运用主要是指运用函数的知识、思想和方法综合分析、解决相关数学问题.学习了函数,同学们在函数的综合运用方面应达到哪些要求呢?

1 准确理解、熟练运用,深化函数基础知识

函数的基础知识也是每年高考考查的基本知识,而且往往可与其他许多知识点交会在一起综合考查.因此,关于函数的基础知识我们一定要引起高度重视,真正做到准确理解、熟练掌握.

例1已知y＝f(x)是偶函数,在[1,2]上单调递减,在[2,3]上单调递增,且当x＞0时,f(x)＝x＋若当x∈[－3,－1]时,n≤f(x)≤m 恒成立,求m－n的最小值.

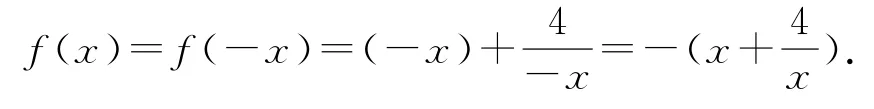
又由题设及偶函数的图象关于y 轴对称,易知函数f(x)在[－3,－2]上单调递减,在[－2,－1]上单调递增.于是,当x∈[－3,－1]时,

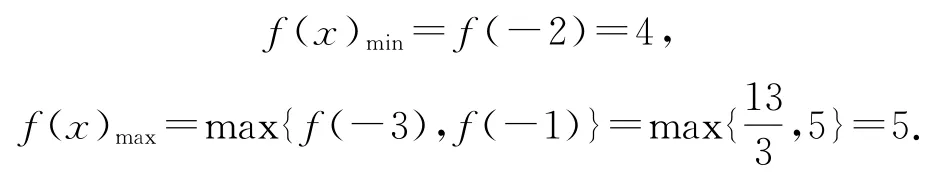
从而,在[－3,－1]上函数f(x)的值域为[4,5].故由“当x∈[－3,－1]时,n≤f(x)≤m 恒成立”得[4,5]⊆[n,m],(m－n)min＝5－4＝1.

求解本题的关键在于将题设所给奇偶性、单调性加以灵活运用.

2 掌握研究函数的方法,提高解题能力

高中数学对函数的研究理论性加强了,对一些典型问题的研究十分重视,如求函数的定义域、确定函数的解析式、判断函数的奇偶性、判断或证明函数在指定区间的单调性等.

例2已知定义在R上的函数f(x)满足:

① 对任意x,y∈R都有

② 当x＜0时,f(x)＞0,f(1)＝－2.求f(x)在[－8,8]上的最小值和最大值.

任取x1,x2∈R,且设x1＜x2,则因为x1－x2＜0,所以由条件②得f(x1－x2)＞0.

于是,由条件①可得

则f(x)在R上为减函数,从而必有f(x)在[－8,8]上也为减函数.

在条件①中,取x＝y＝0,则有f(0)＝f(0)＋f(0)⇒f(0)＝0;取y＝－x,则有f(0)＝f(x－x)＝f(x)＋f(－x),于是,f(x)＋f(－x)＝0⇒f(－x)＝－f(x)⇒f(x)为奇函数.故函数f(x)在[－8,8]上的最大值为f(－8)＝－f(8)＝－8f(1)＝－8×(－2)＝16,最小值为f(8)＝－16.

若不明确抽象函数的性质,则应先根据题设充分挖掘隐蔽的抽象函数的性质(单调性、奇偶性、周期性等),然后再加以灵活运用.

3 抓住函数、方程、不等式之间的相互联系

函数、方程、不等式是相互联系的.对于函数f(x)与g(x),令f(x)＝g(x),f(x)＞g(x)或f(x)＜g(x),则分别构成方程和不等式,因此对于某些方程、不等式问题用函数观点分析是十分有益的.

例3若方程2a·9x＋4a·3x＋a－8＝0 在[－1,1]上有实数解,求实数a 的取值范围.

“方程有实数解,求参数的取值范围”问题,往往可通过分离参数法将问题等价转化为求相应函数的值域问题.