等周长屈服准则求解三维锻压力
2020-12-08李寅雪章顺虎邓磊
李寅雪,章顺虎,邓磊
(苏州大学 沙钢钢铁学院,江苏 苏州 215021)
近些年来金属锻压成形相关的研究主要集中于FEM[1—4]和 BET[5]等数值模拟[6]。遗憾的是,近二十年来鲜有关于含外端影响的三维锻压力的解析报道。由于求解锻压力依赖的Mises 屈服准则是非线性的[7—8],因而获得相应力学参数解析解十分困难,因此,如何用线性屈服准则代替非线性的Mises 屈服准则,进而求得锻压力的解析解是一个值得研究的方向。
Tresca[9]首先提出了一个线性屈服准则,但该屈服准则只考虑了两个主应力的影响,通常给出力学参数的下限解。Hill[10]在1950 年通过对Mises 屈服准则进行逼近,提出了一个线性屈服准则,该屈服准则与Mises 屈服准则的相对误差仅为8%。20 世纪,Yu[11],Huang 和Zeng[12]等提出了双剪应力屈服准则。该准则通常给出力学参数的上限解。最近,章顺虎等[13]开发了一个高度逼近Mises 屈服准则的线性屈服准则,称为EP 屈服准则(等周长屈服准则),该准则为求解复杂的成形力学问题创建了良好条件。
为解决Mises 准则难以获得三维锻压力解析解的问题,文中将采用EP 屈服准则对三维锻压过程进行分析,推导锻压力解析解,并讨论锻压过程塑性变形规律,包括锻压工件初始宽厚比b0/h0、初始长厚比l0/h0、摩擦因数m以及宽展与压下的比值a对应力状态系数nσ的影响。
1 传统屈服准则及比塑性功率
Tresca 屈服准则[9,14](1864)及其比塑性功率数学表达式为:
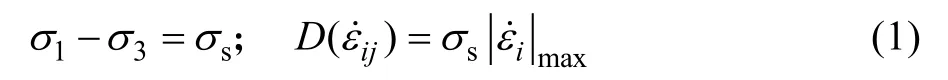
式中:σs为材料的屈服应力;为比塑性功率;为应变速率分量。
Mises 屈服准则[7](1913)及其比塑性功率数学表达式为:
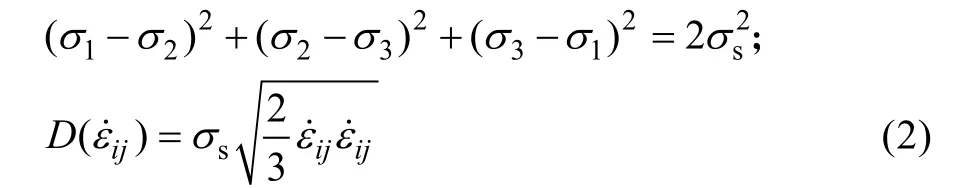
俞茂宏1983 年提出的TSS(双剪应力)屈服准则及其比塑性功率为[9—10]:

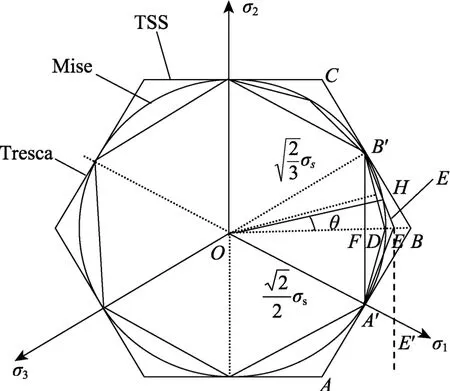
图1 π 平面上的各种屈服轨迹Fig.1 Various yield loci on the π-plane
上述屈服准则在π 平面的屈服轨迹如图1 所示,Mises 屈服准则的轨迹是一个圆,Tresca 屈服准则的轨迹是Mises 圆的内接正六边形,而TSS 屈服准则的轨迹则是Mises 圆的外接正六边形。
一般来说,为了建立总功率泛函的表达式,必须对进行积分,而通常很难得到非线性被积函数的解析解。式(3)在金属成形能量分析中的一些应用表明[15—16],使用式(3)得到的计算结果通常比使用式(2)得到的结果要大。
2 EP 屈服准则及其比塑性功率
如图1 和图2 所示,Tresca 屈服轨迹上的偏应力矢量沿着直线B'F由OB'向OF移动,TSS 屈服轨迹上的偏应力矢量沿着直线B'B由OB'向OB移动,而在Mises 屈服轨迹上的偏应力矢量则是沿着弧线B'D由OB'向OD移动。EP 屈服准则的轨迹满足以下条件:在直角三角形FB'B中B'E是一条直线,并且与圆弧B'D相交;直线B'E的长度与Mises 弧长B'D相等。
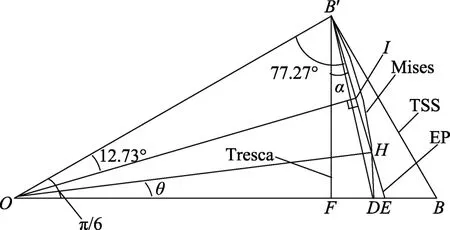
图2 EP 屈服准则的屈服轨迹在π 平面上的几何关系Fig.2 Geometrical relationship of EP yield criterion’s yield loci on the π-plane
根据上述条件,可以得到EP 屈服准则的数学表达式为[13]:

与式(3)的比塑性功率相比,其相对误差为:
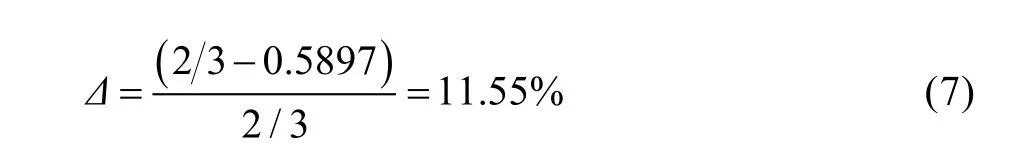
式(6)很好解释了使用TSS 屈服准则得到的计算结果偏大的原因。同时,通过对比式(2)和式(6)可见,式(6)的比塑性功率因其具备线性的特点而容易进行积分求解,因而为变形功率解析式的获得提供了条件。
3 锻压速度场
两个平行压头之间三维锻压如图3 所示。压头视作刚体,工件为刚塑性材料。考虑到锻压变形区的对称性,以下只对变形区的1/8 进行分析。

图3 三维锻压的变形区示意图Fig.3 Deformation zone of three-dimensional forging
假设:

式中:a为宽展与压下的比值。
式(8)两边同除以时间增量Δt,得到:

设速度分量vz随z轴线性变化,则有:
设图3 中自由边界为抛物线形状,宽度b表示为:

式中:Δb1=b1−b0为锻压前后轧件的宽度差值。
式(11)两侧除以Δt可以表示出轧件宽度的变化函数,即:

让vy随y坐标线性变化,得到

可以利用式(16)的值计算应变速率和速度场各分量的比值。应变率张量的特征方程只有当下面的行列式的值为零时才有唯一解,即:

3 总功率和锻压力
3.1 内部变形功率
将式(18)代入式(6),并积分,可得:
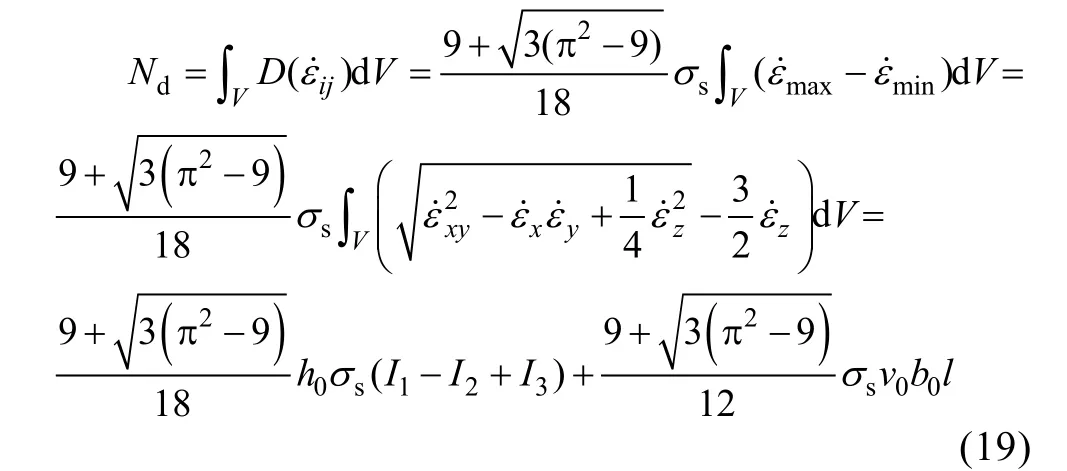
式中:I1,I2,I3分别为应变率向量内积的逐项积分。将式(16)的值代入以下分数的分母,积分得到:

3.2 摩擦功率

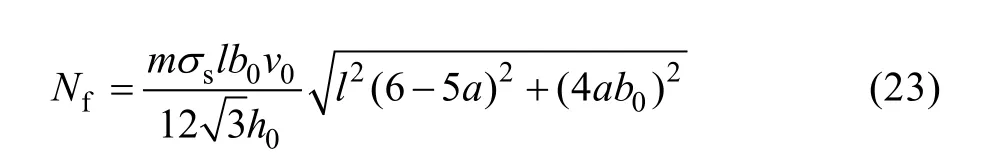
3.3 剪切功率
在变形区与工件外端交界面上,速度不连续量和和剪切功率分别为:
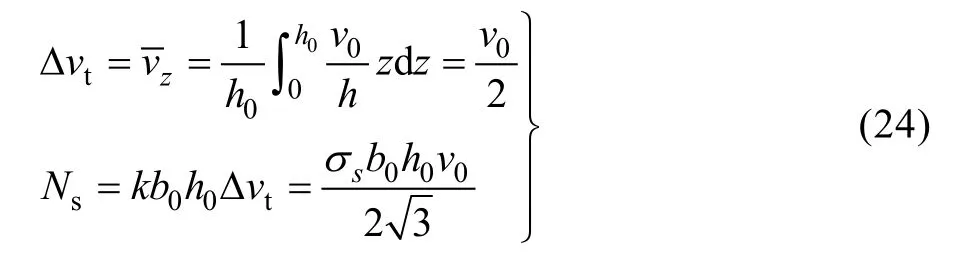
3.4 总功率和锻压力
令外功率与上界总功率相等,则有:

将式(20,23—24)代入式(25)后重新整理可得:

式(26)表明,应力状态系数nσ是l/h0,b0/h0,m和伪独立参数a的函数。
考虑到对称性,因此总压力表示为:

摩擦因数m的值可以用式(28)的Tarnovskii方程来计算:
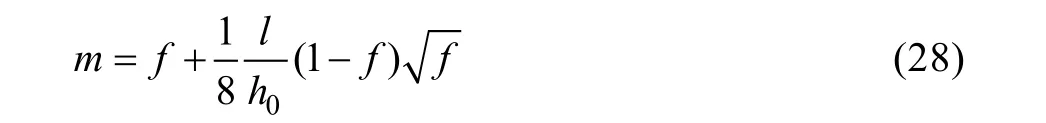
式中:f为库伦摩擦因数。
从式(8)易知,a的值表示为:

式中:Δb1=b1−b0为最大宽度点上所测得的宽展,而ε=Δh/h0为该道次的压下率。
4 实验验证
在东北大学轧制技术与连轧自动化国家重点实验室使用200 kN 的万能材料试验机进行了锻压试验。以不同的压头和压下量为变量对3 组纯铅试样进行压缩。压头速度为15~30 mm/min。样本编号及其试验数据如表1 所示,Pm为实测总压。
根据式(29)得到的a值和根据式(26)得到的计算结果如表2 所示。

表1 样品尺寸及测试数据Tab.1 Sample size and tested data

表2 通过测量a 值(m=0.3)得到的计算结果Tab.2 Calculated results by measured a (m=0.3)
以压力测试的第二道次为例,具体计算过程如下:根据表1 可得,ε=(9.85−8.745)/9.85=11.22%,l/h0=1.5228,a=0.5144,f=0.23。根据式(28)可得m=0.3。将第二道次所有的数据代入式(26—27)易得nσ=1.3074,P=32.59 kN,它与Pm的相对误差为Δ=(32.59−30)/30=8.6%。在以上的计算中,通过t=2Δh/v=4.42 s,可得ε˙=0.112/t=0.025 s−1,ε=11.2%,从而查得材料的屈服应力为σs=20.26 MPa[17]。其他试样的计算过程同上。
从表2 可以看出,计算得到的总压力值P大于测量的压力值Pm,并且它们之间的相对误差在8.6%~10.5%之间,小于工程允许误差15%。可见,基于EP 屈服准则和所提出的速度场得到的理论锻压力是可行的。
图4 为初始宽厚比b0/h0=3 时不同轧件长厚比l/h0和摩擦因数m对应力状态系数nσ的影响。nσ随着m的增加而增加,随着l/h0先减小后增加,并且在给定的m时都能获得最小值。
图5 为l/h0=3 时不同初始轧件宽厚比b0/h0和摩擦因数m对应力状态系数nσ的影响。可见,nσ均随着m和b0/h0的增大而增大。
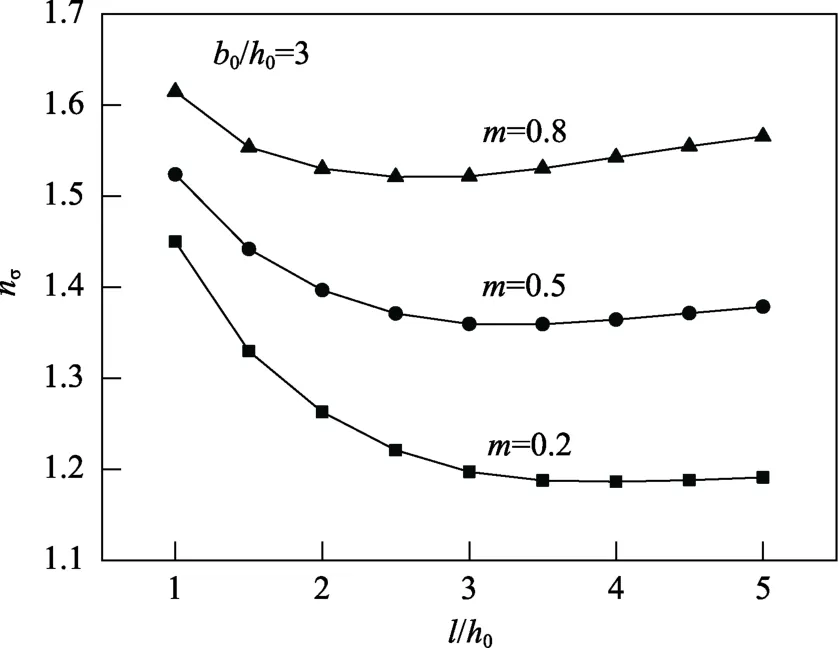
图4 不同m 值下l/h0 对nσ 的影响Fig.4 Effects of m and l/h0 on nσ

图5 不同m 下b0/h0 对nσ 的影响Fig.5 Effects of m and b0/h0 on nσ
图6 为b0/h0=3 时不同轧件长厚比l/h0和摩擦因数m对a的影响。可见,a随着l/h0的增加而增加;随着m的增加,a的值不断减小,然而,随着l/h0的增大,不同m时a值之间的差值逐渐减小。当l/h0≥2.5 时,所有曲线的a值均相等,此时,m对a的影响可以忽略不计。
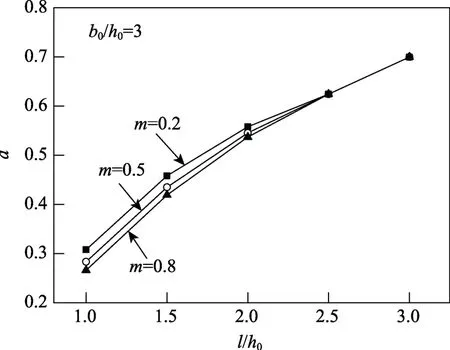
图6 不同m 下l/h0 对a 的影响Fig.6 Effects of m and l/h0 on a
图7 为l/h0=3 时不同轧件宽厚比b0/h0和摩擦因数m对a的影响。随着b0/h0值的增加,a值逐渐减小。当b0/h0≥1.5 时,m对a值的影响变大。

图7 m 和b0/h0 对a 的影响Fig.7 Effects of m and b0/h0 on a
5 结论
1)基于EP 屈服准则和文中所构建的速度场,获得了应力状态系数nσ的解析解,它是关于初始长厚比l/h0、初始宽厚比b0/h0、摩擦因数m以及宽展-压下比值a的函数。
2)对比锻压力的理论值和实测值后发现,理论值比实测值高 8.6%~10.5%,仍小于工程允许误差15%,从而表明,基于EP 屈服准则和所提出的速度场得到的理论锻压力是可行的。
3)nσ随着m的增加而增加,随着l/h0的增加先减小再增加,并且在m给定时获得最小值;a随着l/h0的增大或者b0/h0的减小而增大,并且当l/h0≥2.5 或者b0/h0≤1.5 的时候,无论m为何值,a的值都趋于相等。
