SPRC340S 金属在不同应变率下的本构模型评估

尚宏春，武鹏飞，娄燕山

（西安交通大学 机械工程学院，西安 710049）

随着机械设备向着高速化、强韧化方向发展，人们对材料性能的要求也不断提高，材料的应用领域日趋广泛，使用条件也逐渐趋于极端化，例如切削、喷丸等高速制造领域、汽车经受高速碰撞过程、高速弹丸和弹片的变形等[1—8]。为了确保高速变形下有限元分析的可靠性，必须准确了解材料在各种应变率下的力学特性。材料的屈服应力、强度和硬化行为容易受到应变率的影响，这被认为是材料的固有特性。当金属材料在动态载荷下变形时，惯性效应和应力波传播导致不同材料对应变率的敏感程度有着显著的变化。材料的动态行为是其本身的固有特性，所以仍没有哪个本构模型能够准确描述不同类型的材料应变率效应。有限元模拟结果精确与否，往往取决于模拟过程中是否采用了一个精确的、能够反映材料在动态载荷下力学行为的本构模型。许多研究人员提出了各种本构模型，以有效表示各种金属材料的应变率硬化特性[9—10]，因此，选择能够描述材料应变率硬化特性的最佳模型，以便得到可靠的有限元模拟结果，正确指导金属构件的设计和优化。

文中通过准静态试验和高速拉伸试验测试，获得SPRC340S 金属材料在不同应变率下的真应力-真塑性应变曲线，并研究了6 种经典本构模型对于该金属材料应变率敏感性描述的准确性及适用性。通过对比本构模型的预测结果与试验结果以及均方根误差，得到最适用于SPRC340S 金属材料的应变率硬化模型。

1 应变率硬化模型回顾

多种硬化模型被提出来以描述应变、应变率和温度对金属材料硬化特性的影响。在近几十年，人们或提出或改进了许多本构模型，并用这些模型来描述塑性流动行为对状态变量的依赖性。对于最初的本构模型，通常是针对特定材料而提出的，或多或少存在一定的局限性。随着其他研究者不断对最初本构模型进行改进，模型才得以进一步完善。根据其建模特点，本构模型可被分为两类：唯象型本构模型和物理型本构模型。唯象型本构模型是一类对材料硬化行为进行经验性定义的本构方程，其主要特点是本构模型参数较少，因而易于在数值仿真中应用，例如Johnson-Cook（JC）模型、Modified Khan-Huang（Mod KH）模型、Modified Johnson-Cook（Mod JC）模型、Lim-Huh（LH）模型等。物理型本构模型能够反应材料的宏观状态变量及微结构演化特性，几乎所有的物理型本构模型在建模时都引入了热力学理论、热激活位错运动理论以及滑移动力学理论，例如Zerilli-Armstrong（ZA）模型，这些本构模型将按提出的时间先后顺序逐一介绍。

1.1 Johnson-Cook 模型

Johnson 和Cook 在1983 年[11]提出了一种应变率硬化模型，该模型能够表示应变、应变速率和温度对金属屈服应力的影响，如式（1）所示：

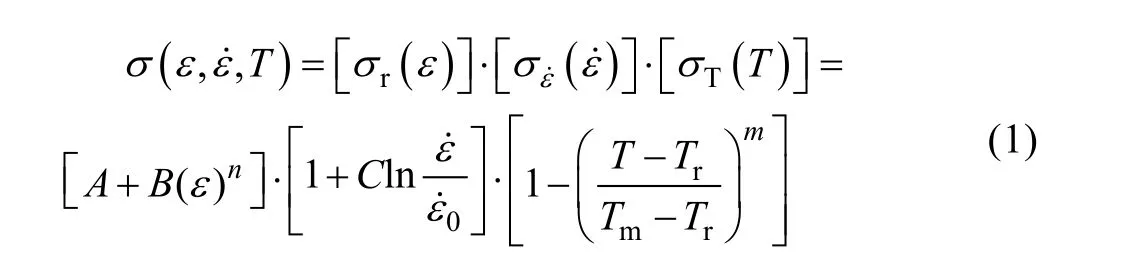
式中：ε表示等效塑性应变；表示无量纲塑性应变率；T，Tr和Tm分别表示热力学温度、参考温度和金属熔化温度；A，B，n，C和m分别是模型的5 个常数；表达式的第一个括号表示在室温和参考应变率下应力对于应变的函数关系；表达式的第二项和第三项分别表达了应变率和温度对应力的影响。由于JC 模型具有参数较少、形式简单的优点而被广泛应用于计算机仿真模拟程序中，但是模型仍然存在以下几个缺点：①模型第二个括号的应变率硬化项表示为应变率对数的线性函数，导致模型的屈服应力只能随应变率的对数线性增加，但是对于多数金属材料，其应变率效应并不是简单的线性关系可以描述的；② 该模型没有表达应变率和应变的耦合关系，只是简单通过应变项与应变率项相乘来表示应力-应变关系随应变率的变化，随着应变率的增加，应力-应变曲线的斜率增大或者减小是晶体结构的固有属性[12]，然而，在该模型中，由于模型的性质，应力-应变曲线的斜率随着应变率项的增大而成比例增加。

1.2 Zerilli-Armstrong 模型

基于位错机制，Zerilli 和Armstrong 在1987 年[13]提出了一个应变率本构关系，来分别描述了体心立方结构（BCC）和面心立方结构（FCC）金属的应变率强化行为：

式中：C0，C1，C2，C3，C4，C5是材料常数，C0被定义为。ZA 模型针对BCC 和FCC 晶体结构材料的硬化特性，提出了两种不同的表达形式。对于FCC 结构材料的本构方程，考虑的主要因素是屈服应力的温度软化和应变速率硬化相关性随应变的增加而增大。对于BCC 结构材料的本构方程，应变硬化项与应变速率和温度无关。在两个不同的ZA 模型的表达式中，可以观察到每个模型的缺点。对于FCC 结构材料的本构方程，C0与应变率和温度无关，即屈服应力不随应变率和温度的变化而变化。对于BCC 结构材料的本构方程，应变硬化因子没有耦合应变速率硬化和温度软化效应，所以BCC 模型没有显示出随应变率和温度的变化而发生的硬化特性。

1.3 Modified Khan-Huang 模型

式（3）的Khan-Huang 模型由Khan 和Huang 在1992 年[14]提出，用来描述由应变率引起的硬化变化，其中

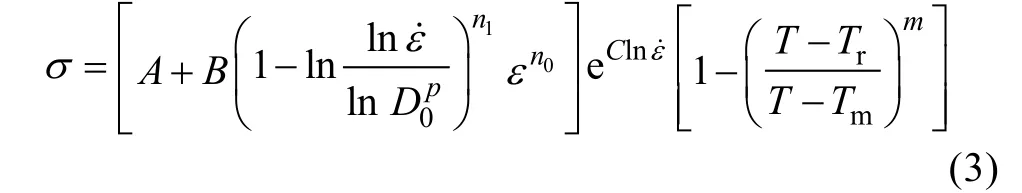
第一个括号中的应变硬化项由应变和应变率的耦合函数描述。描述应变硬化行为的参数B由应变率的函数表示，而在JC 模型中的参数B被视为常数。该表达式可以克服JC 模型的缺点，应变硬化参数B可以随着应变率的增加而减小。对于JC 模型，应变硬化项没有考虑应变率的变化，但在该模型中可以通过参数n1来控制。Khan-Huang 模型的应变率强化项表示为，该项可以转换为，它以应变率的指数表示材料的应变率硬化行为，但一般的金属材料与应变率的对数呈指数关系。Song 和Huh 在2007 年[15]通过修改Khan-Huang 模型中的应变速率硬化项，在式（4）中提出了改进的 Khan-Huang 模型，其中，第一个括号中的应变硬化项与Khan-Huang 模型中的相同，第二个括号中的应变率硬化项与改进的JC 模型中的相同。改进的模型结合了两个模型的优势，对材料的加工硬化效应有了更为准确的描述。

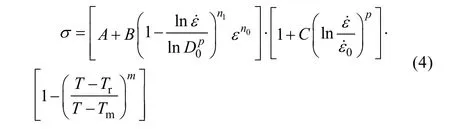
1.4 Modified Johnson-Cook 模型

Kang 等在1999 年[16]通过修改JC 模型的应变率硬化项，改进了传统的JC 模型。JC 模型中的应变率强化项的线性表达式被指数表达式替代，如式（5）所示：

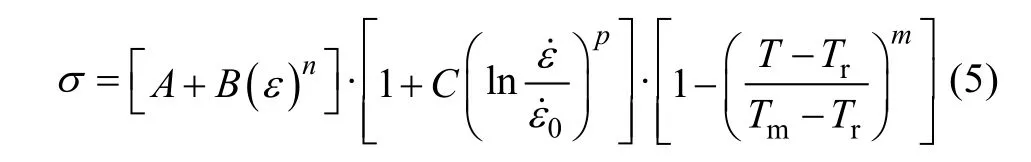
1.5 Lim-Huh 模型

Huh 等在2014 年[17]总结了4340 钢、OFHC 铜和Ti6Al4V 合金在不同应变率下的试验结果，并比较和验证了不同类型的应变率硬化模型。尽管改进的Khan-Huang 模型可以描述实际的应变率强化，即随着应变率的增加而降低，但是，该模型表明，随着对数应变率的增加，应变是一个线性减小的函数。由于线性表达式，应变硬化的表达式仍然存在一些限制。为了准确表示应变硬化行为随着应变率对数的增加而产生的变化，提出了LH 模型。尽管LH 模型具有出色的拟合结果，但是随着应变率的增加，屈服应力会减少或保持恒定，而且该模型在高温下的硬化行为存在一些缺点。为了表现出高温下的热软化作用，Piao 等[18—19]在LH 模型中增加了涉及应变率的热软化项，见式（6）：

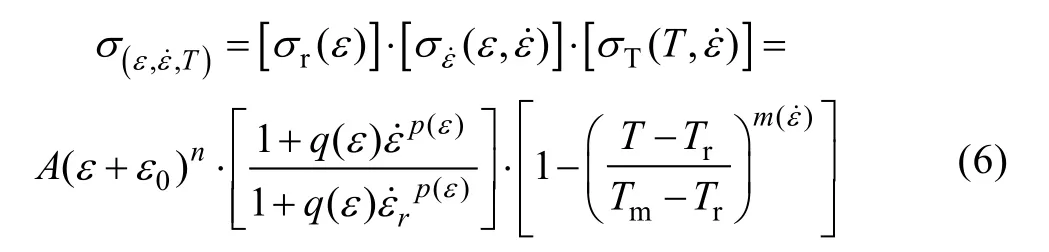
2 单向拉伸试验

文中所用SPRC340S 材料的应变率硬化特性是通过准静态单向拉伸试验和高速拉伸试验获得的。使用 INSTRON 万能试验机进行了准静态应变率（0.003～0.1 s−1）的单轴拉伸试验。使用高速拉伸试验系统获得材料在高应变率下的硬化特性（1～500 s−1）。通过试验测得的力-位移关系，取最大力或颈缩之前的力-位移曲线，计算材料在不同应变率下的硬化行为。文中所测得的SPRC340S 在不同应变速率（0.003～500 s−1）下的真应力-真塑性应变曲线如图1 所示，可以发现该材料屈服应力随应变率的增大而变大，是正应变率效应材料。

3 结果与讨论

通过优化算法，标定了文中所研究的6 类应变率强化模型。标定后的参数如表1 所示。标定后的硬化模型预测了材料在不同应变率下的硬化特性，并与试验结果进行了对比，如图1 所示。通过拉伸试验测得的SPRC340S 硬化曲线和每个模型的预测结果对比发现，JC 模型和BCC 型ZA 模型由于屈服应力表达不当，其硬化特性出现了明显的偏差。FCC 型ZA 模型的预测结果，随着应变率的增加，硬化行为也会增加，但是，该模型的拟合结果与试验结果依然存在较大误差，因为该模型不能描述屈服应力随应变率的变化而变化。修正后的JC 模型也显示出较大偏差，因为模型中的屈服应力变化是由参考应变率为0.001 s−1时屈服应力的等比例扩大或缩小获得的。修正后的Khan-Huang 模型和LH 模型都表现出很好的拟合效果，因为它们能够准确地拟合屈服应力相对于应变率和应变的变化。

文中通过均方根误差对各个模型的标定结果做了定量分析，结果如图2 所示，可以发现误差最大的模型为ZA（FCC）模型，预测误差达到1.1682。该模型预测误差最大的主要原因是：SPRC340S 为BCC 结构。JC 模型预测的误差值为0.5056，与ZA（FCC）相比较，误差值只有前者的一半。这些模型中预测精度最高的模型为LH 模型，误差只有0.0024，因此，LH 模型最适用于表征SPRC340S 金属应变率强化特性。

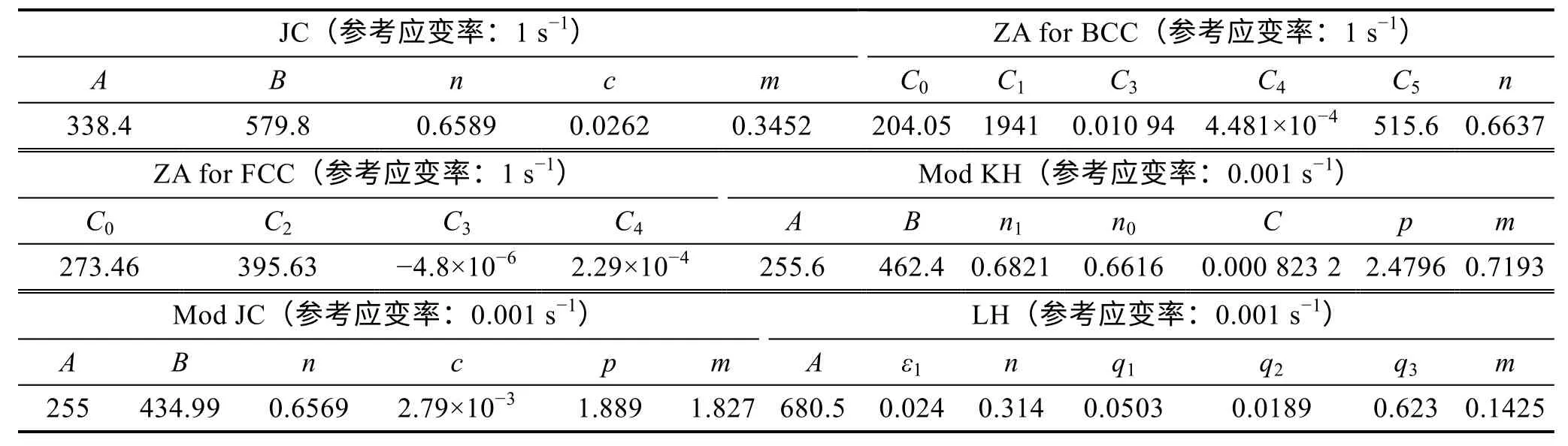
表1 应变率强化模型标定参数Tab.1 Calibration parameters of strain rate hardening model

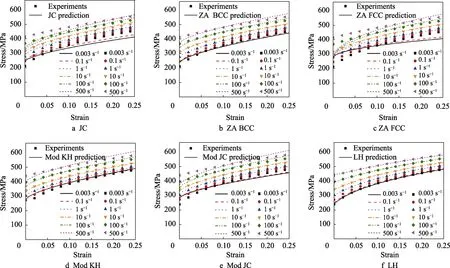
图1 使用分步标定法拟合SPRC340S 合金在不同应变速率下真应力-应变曲线Fig.1 True stress-strain curve of SPRC340S alloy fitted by stepwise calibration at different strain rates

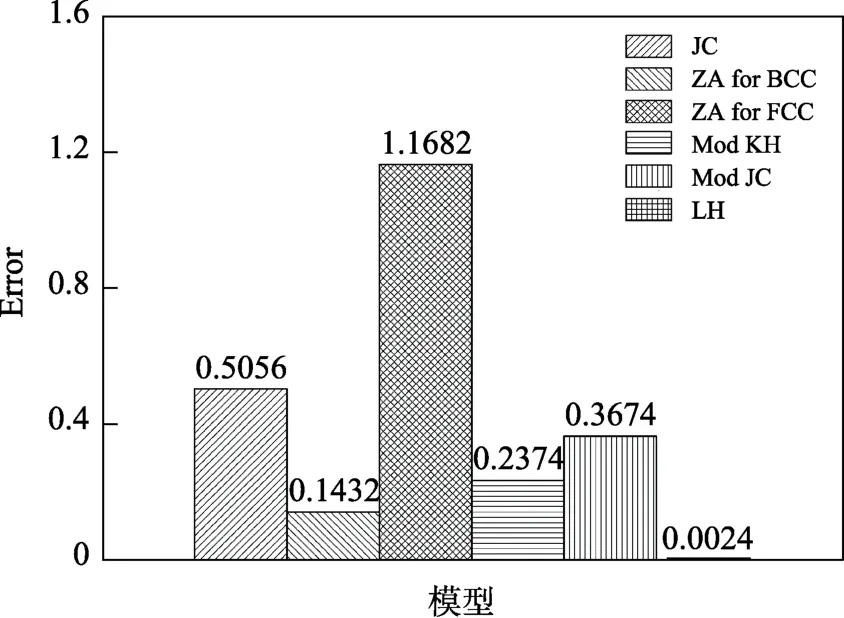
图2 不同模型标定结果的误差对比Fig.2 Comparison on calibration result error of different models

4 结语

从SPRC340S 金属材料的动态行为的角度出发，比较分析了6 种应变率硬化模型的特性，并评估了应变率强化模型的适用性。通过对比拟合误差，发现Lim-Huh 模型是最适合描述SPRC340S 应变率强化特性的模型。Johnson-Cook 模型和 FCC 型 Zerilli-Armstrong 模型在屈服应力和硬化特性的表征上存在重大缺陷。修改后的Johnson-Cook 模型的硬化结果也不准确。BCC 型Zerilli-Armstrong 模型仅限于其硬化特性不会随应变率变化的材料。