宏压电纤维致动的水下推进器性能及机理*
2020-12-08林煌旭任枭荣娄军强
林煌旭, 任枭荣, 娄军强, 2, 贾 振
(1.宁波大学机械工程与力学学院 宁波,315211)
(2.浙江大学浙江省先进制造技术重点实验室 杭州,310027)
引 言
随着陆地资源的日益枯竭,蕴藏着丰富矿产资源的海洋是维持人类可持续发展的重要空间。模拟海洋生物的仿生水下推进器拥有出色的流体动力学性能,具有推进效率高,机动性强且隐蔽性好的优点,在海洋环境监测、生物观察及资源勘探领域具有广阔的应用前景[1]。以鱼类为代表的海洋生物进化出了卓越的水下运动能力。近85%的鱼类都采用了身体/尾鳍推进方式[2]。BCF模式的鲹科鱼类推进效率可超过90%,是迄今为止鱼类演化出的效率最高、速度最快的推进模式,被认为是未来水下推进装置的最终设计目标[3]。
早期的仿生水下推进器多采用电机、气/液压等常规驱动元件,配合铰链、连杆机械传动机构来模仿鱼的躯干及尾部的摆动。但是复杂庞大的传动机构导致推进器动作生硬、柔度不高,推进效率难以媲美模仿的鱼类。智能材料发展为水下驱动技术提供了新的途径[4]。智能材料可与基体结构直接集成,实现“近零驱动”。采用智能材料驱动的仿生推进器打破了传统驱动方式的限制,表现出较大的柔性,从而较好地模拟鱼类复杂的运动。研究者将压电材料[5]、形状记忆合金[6]以及离子导电聚合物材料[7]等智能材料成功地用于新型水下仿生机器鱼的驱动和推进,证实了智能材料在水下推进领域的巨大优势。近年来,美国国家航空航天局率先研制出了宏压电纤维复合材料,MFC展示出了柔性好、变形大且驱动力强等优点,在水下仿生推进系统中具有广阔应用前景[8]。但是由于智能材料驱动的水下推进系统研究尚处于起步阶段,目前研究大都止于可行性验证阶段,研究重点在于驱动方法可行性和方案可实现性,对整个仿生推进系统的驱动特性和推进机理缺乏深入研究[9]。
文中在描述MFC结构的基础上,根据鲹科鱼类的游动方式和特点,提出了一种宏压电纤维致动的仿鲹科水下推进器。搭建了推进器性能测试平台,分别对推进器在空气中和水下的摆动性能进行了实际测试。基于实验测试结果,采用计算流体力学研究了推进器摆动过程中的流场特性和尾迹旋涡的分布情况,得到了推进器在不同摆动时刻瞬态流场的涡量云图以及速度矢量的变化情况,揭示了提出的仿生推进器的流体动力学机制和推进机理。
1 MFC致动的水下推进器结构描述1.1 MFC的基本构成
宏压电纤维复合材料是由美国Langley研究中心研发的新型压电纤维复合材料[10]。MFC按照一定的比例成分和空间排布形式将矩形横截面的粗压电纤维和树脂基体胶合在一起,同时采用特殊工艺将指交叉电极蚀刻在包铜聚酰亚胺薄膜上,其结构示意图见图1。树脂基体增强了MFC结构的强度和韧性;指交叉电极排列方式增加了压电陶瓷与电极之间的接触面积,大幅度提高了MFC的变形和驱动能力;最外层的聚酰亚胺薄膜能保证其密封性和防水性。与传统的压电陶瓷相比,MFC具有柔性更好、驱动变形量大且能量转换效率高等一系列优点,因此特别适合作为水下推进器的驱动元件。
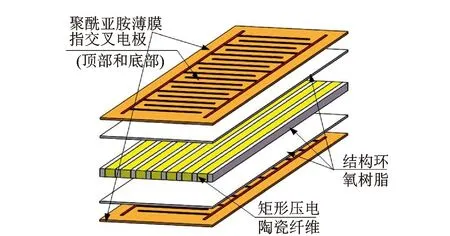
图1 MFC结构示意图Fig.1 Structure diagram of MFC actuator
1.2 仿鲹科谐振式水下推进器结构
鲹科鱼类自主游动过程中,头部和胸部的横向位移几乎可以忽略,可将其身体大约2/3部分视为刚体,其巨大的推进力主要是尾部摆动产生。鲹科鱼类BCF谐振式推进模式中,其柔性尾部协调身体摆动产生推进力前进,且摆动幅度从身体后部到尾鳍逐渐增大,其尾部摆动产生的推进力占整个身体前进所需推进力的90%以上,其摆动推进过程如图2所示[11]。
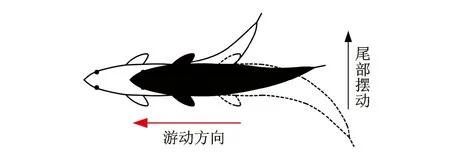
图2 鲹科鱼类BCF谐振式推进过程示意图Fig.2 BCF oscillatory propulsion process for carangiform fish
由于鲹科鱼类在推进过程中头部和胸部基本不动,主要靠尾部带动尾鳍摆动产生推进作用,许多研究者都采用经典的悬臂式Euler-Bernoulli梁模型来模拟鲹科鱼类BCF摆动推进模式,文中建立MFC致动的推进器结构如图3所示[12]。
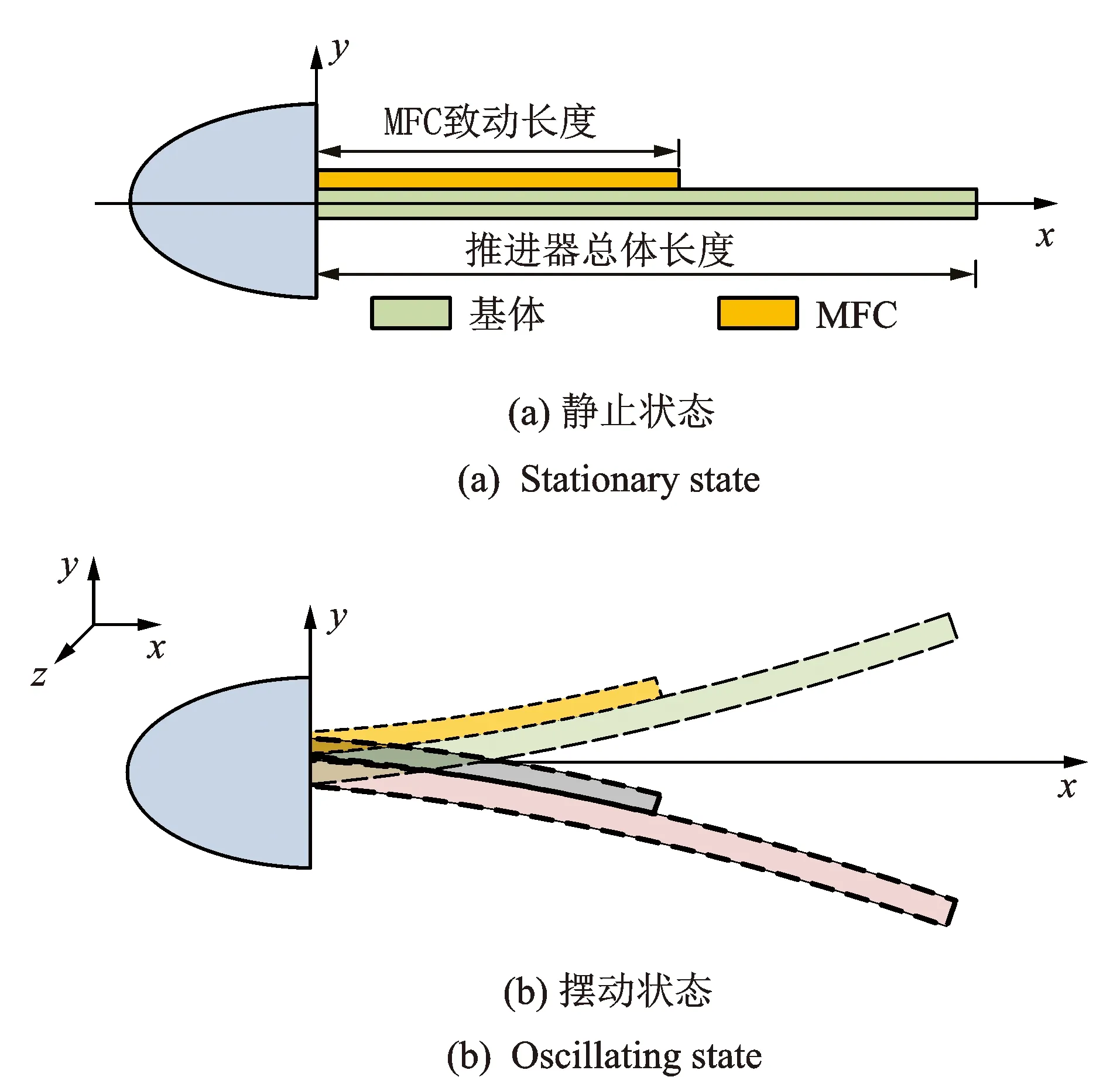
图3 MFC致动的水下推进器结构示意图Fig.3 Structure of the underwater propeller actuated by MFC
如果对MFC施加一定的交变电压,MFC将沿着基体横向方向产生伸缩变形,带动基体材料不断地产生弯曲变形,其中粘贴有MFC的基体部分在MFC带动下主动变形,而没有粘贴MFC的基体部分在主动变形部分的带动下也会发生变形,从而产生类似于鲹科鱼类尾部的摆动运动,进而模拟鲹科鱼类的摆动式推进模式,其结构尺寸参数见表1。
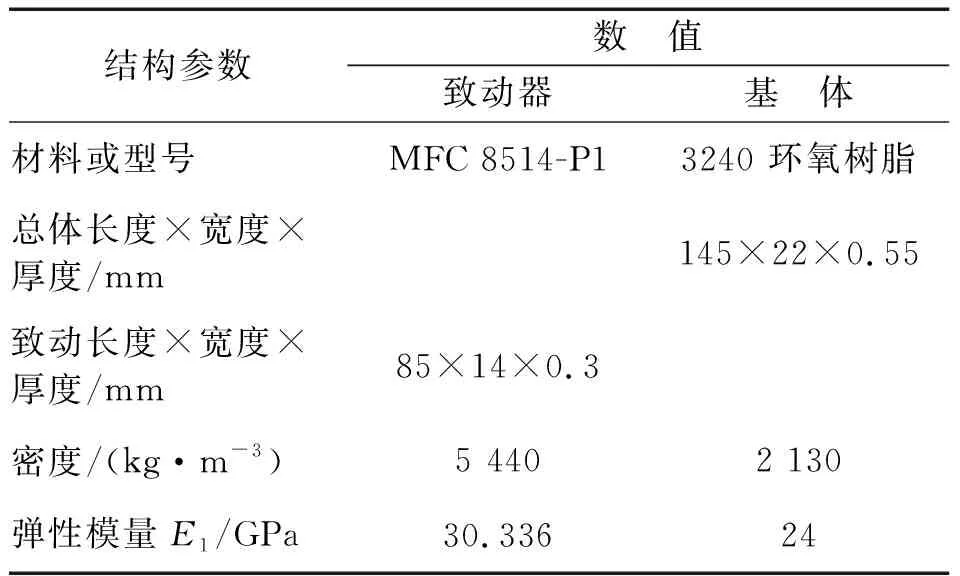
表1 MFC致动的水下推进器结构尺寸表Tab.1 Structural parameters of the underwater propeller
1.3 仿鲹科水下推进器摆动机理
图3(b)中,推进器在x-z平面内的摆动状态是细长体结构特征,理论上常用欧拉-伯努利梁模型来表示推进器模型的弯曲变形[13]。
其运动方程描述为
(1)
其中:ρ为推进器材料的等效密度;A(x)为等效横截面积;EI(x)为弯曲刚度;F(x,t)为MFC驱动力和流体载荷共同作用的合力。
由于推进器前身基本不动,近似可认为其满足一端固定,一端自由的悬臂梁边界条件为
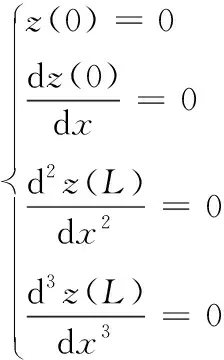
(2)
利用假设模态法和悬臂梁边界条件确定推进器各阶主振型函数为
zr(x)=chβrx-cosβrx+ξr(shβrx-sinβrx)
(3)
其中:ξr=-(chβrL+cosβrL)/(shβrL+sinβrL);zr(x)为推进器在第r阶振型时的横向位移。
2 推进器性能测试系统搭建
仿生推进器的摆动行为直接决定了推进器的推进性能,为了测试MFC致动器的致动效果,搭建了推进器性能测试系统如图4所示。实验中压电纤维采用美国Smart Material Corp.生产的d33模式MFC,型号为MFC 8514-P1,并用环氧树脂胶水DP-460将MFC与梁基体进行粘贴。
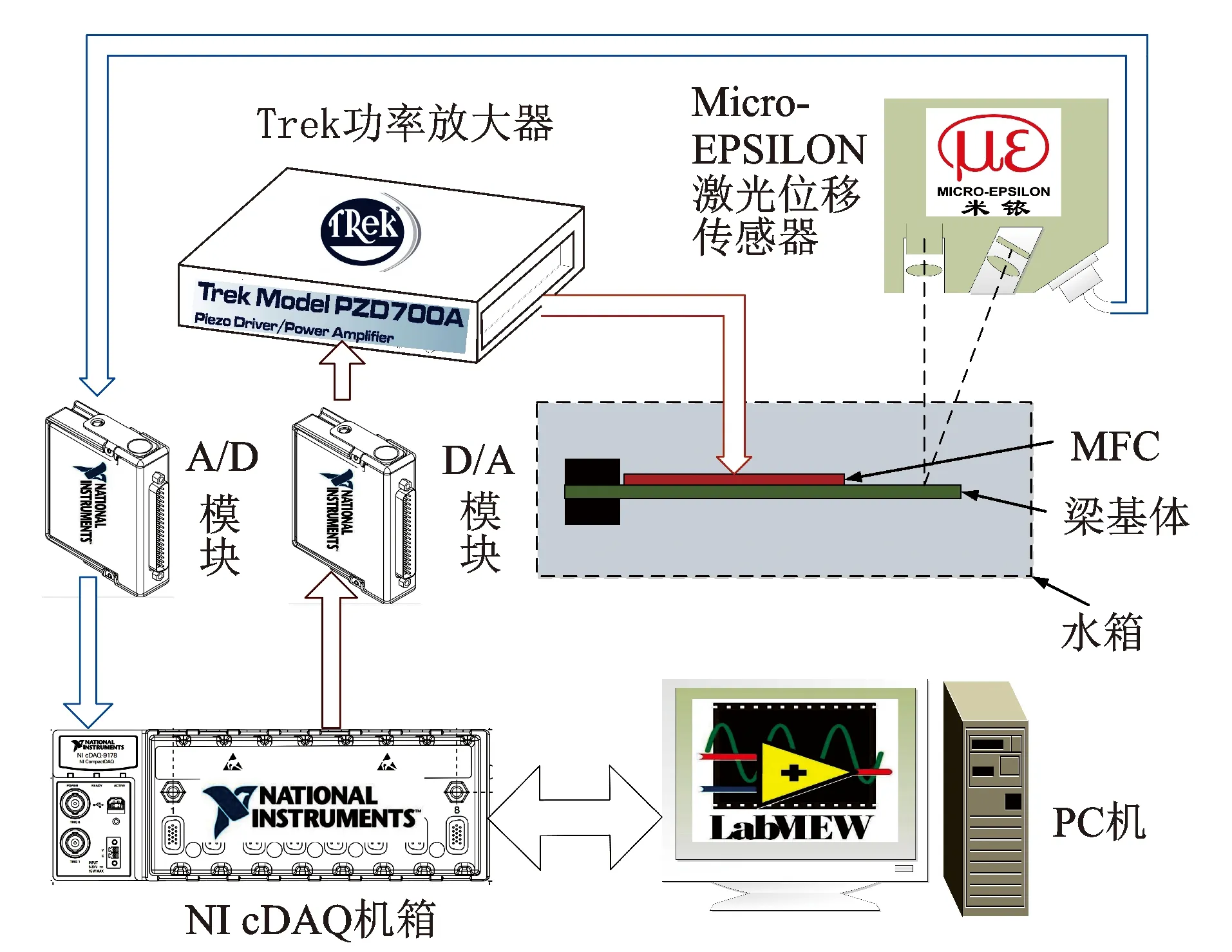
图4 推进器性能测试系统结构框图Fig.4 Block diagram of the underwater propeller system
推进器性能测试过程中,控制平台发出控制信号到嵌入式机箱CompactDAQ (NI, cDAQ-9178),通过电压输出模块(NI, AO9263)输出并经高压功率放大器(Trek,PZD700A,放大增益200)放大,最后施加到MFC上,从而驱动MFC按照设定的控制规律实现推进器的摆动运动;同时利用布置在推进器末端的激光位移传感器(Micro-EPSILON, ILD1402-50)实时检测推进器末端的纵向摆动位移,其摆动位移信号通过调理电路转换为1~5 V的电压信号,经电压输入模块(NI, AI9205)采集到cDAQ机箱,最后输送到计算机中。整个测控系统基于NI-LABVIEW平台完成,系统实物装置见图5。

图5 测试系统实物图Fig.5 Experimental setup of the underwater propeller system
3 仿生推进器摆动性能测试
3.1 空气中推进器摆动性能测试
实验中首先通过扫频实验激起推进器的弹性振动以掌握其模态特性。考虑到低阶振动模态在推进器振动特性中的主导地位,采用频率范围0.1~30 Hz,电压峰峰值为800 V的正弦扫频信号施加到MFC致动器上,整个扫频过程持续20 s,采样频率为500 Hz。从空气中推进器扫频实验测试结果中可以看出:MFC致动器作用下,推进器产生了明显的弹性振动,其一阶固有频率为17.7 Hz,摆动幅度峰峰值最大可达35 mm以上。
为了进一步测试推进器在空气中的摆动特性,进行了不同幅值和频率的驱动电压下,推进器末端摆动幅值变化的性能测试实验。考虑到压电纤维致动器的驱动电压范围为-500~1 500 V,实验中施加无偏置、峰峰值分别为200,400,600,800 V及1 000 V,频率范围为12~22 Hz、间隔为1 Hz的电压激励信号到压电纤维致动器上,测得推进器末端振幅随激励电压的变化情况如图6所示。
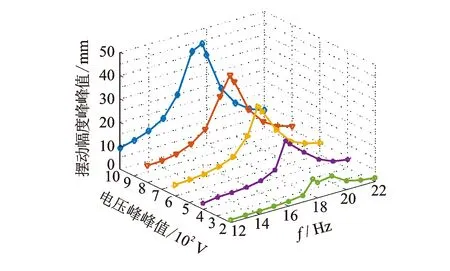
图6 空气中推进器末端摆幅随驱动电压变化实验结果Fig.6 In air experimental result of the oscillatory amplitude with varied driving voltage
从实验结果中可以看出:相同激励电压幅值下,推进器在固有频率处具有最大的摆幅;在峰峰值1 000 V的激励电压下,其空气中的摆幅峰峰值可达45 mm。初步证实了所提出方案的可行性。
3.2 水下推进器摆动性能测试
在周围流体动力学的影响下,推进器结构的固有频率会显著下降。采用流体动力学函数对推进器空气中的固有频率进行修正,可得其水下固有频率表达式[13]为
(4)
其中:ρw为水的密度;ρc为推进器等效密度,由等效体积法确定值为2 689 kg/m3;b和h分别为基体宽度和厚度;Гr为水动力学函数,此处可近似取为1。经计算可得推进器水下固有频率ffluid约为4.9 Hz。
为了掌握水下推进器的低阶模态特性,采用频率范围0.1~7 Hz,电压峰峰值为800 V的正弦扫频信号施加到MFC致动器上。从水下推进器扫频实验末端位移频谱图7中可以看出:其水下固有频率约为4.2 Hz,与修正公式计算结果基本一致。与空气中测试实验相似,同样施加5个不同峰峰值,频率范围为2~7 Hz、间隔为0.5 Hz的电压激励信号到压电纤维致动器,测得水下推进器末端振幅随激励电压的变化情况见图8。
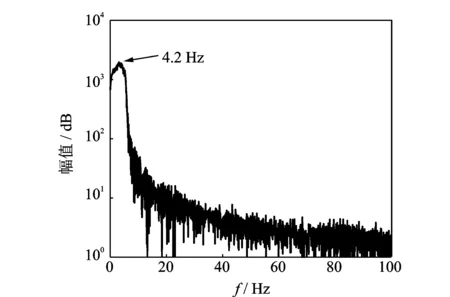
图7 水中推进器扫频实验末端摆动位移频谱图Fig.7 Underwater frequency response of the propeller
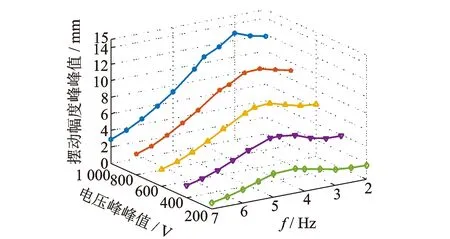
图8 水下推进器末端振幅随驱动电压变化实验结果Fig.8 Underwater experimental result of the oscillatory amplitude with varied driving voltage
显然受周围流体作用力的影响,不仅推进器结构固有频率显著降低,其在相同驱动电压下末端摆动幅度也大幅度下降。在峰峰值1 000 V激励电压致动下,水下推进器最大摆幅的峰峰值仅为13 mm。需要指出的是:实验中水下推进器最大摆幅是在频率为3 Hz的激励电压作用下取得的,明显低于推进器结构的水下固有频率;这是由于压电纤维材料本身的机电耦合特性、迟滞非线性以及流体水动力特性相互影响的结果,随着驱动电压的升高,存在着刚度软化现象[14]。
4 推进器谐振式推进机理分析
仿生推进器通过模拟鱼类BCF摆动方式来实现推进,由于水下推进器的往复摆动属于复杂的流固耦合动力学问题,难以通过理论建模的方法进行分析求解,故此处采用计算流体力学的方法对其摆动式推进机理进行研究。基于ANSYS-FLUENT仿真平台,采用可实现k-ε湍流模型,选择弹簧光顺和局部重构方法相结合的动网格技术来刻画流场的动态变化过程,并设置力函数来定义推进器的往复摆动过程。
CFD仿真分析中建立的计算域和网格划分结果如图9所示。长方体流体域的尺寸为545 mm×222 mm×300 mm,3个方向尺寸都远大于推进器尺寸,从而保证推进器周围的流体能充分发展,最后采用四面体非结构网格对流体域进行划分,获得节点数187 582个。
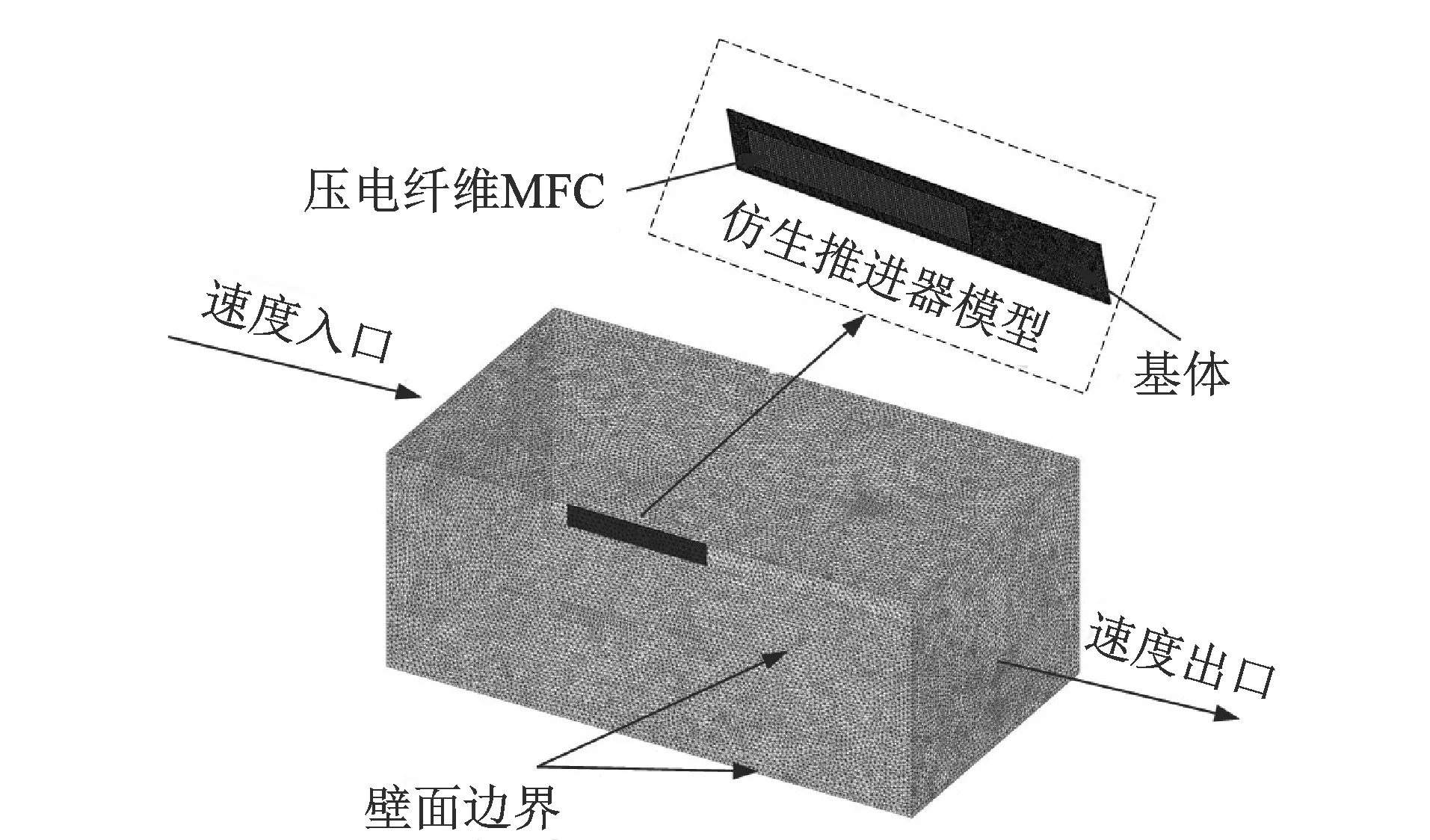
图9 FLUENT中计算域和网格划分结果Fig.9 Computational domain and grid meshing results in FLUENT
4.1 CFD仿真结果分析
由图8可知推进器在峰峰值1 000 V,激励频率4 Hz的激励电压下,摆幅峰峰值达到10.4 mm。故CFD仿真分析中设定推进器的摆动频率为4 Hz,单侧摆幅为5.2 mm;为了便于分析流场结构的数值计算结果,定义推进器末端的摆动位置和摆动相位角的关系如图10所示。定义推进器摆动到最左端,速度为零的时刻为0°相位;推进器摆动到中间位置,向右运动速度最大的时刻为90°相位;同理最右端速度为零时刻为180°相位,向左运动速度最大的中间位置270°相位。
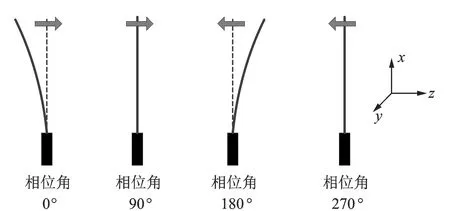
图10 推进器摆动位置和相位角关系图Fig.10 Definition of the phase angle of the oscillating propeller
由于推进器在启动初始阶段与周围流体的耦合效应较为复杂,且处于不稳定阶段,故此处选取推进器摆动35个周期以后的流场稳定变化情况来分析其摆动过程的流场特性。图11给出了静水条件下瞬态流场的涡量云图以及速度矢量图在一个完整摆动周期内的稳定变化情况,其中从相位角0°开始,以45°为间隔,共8个典型相位。
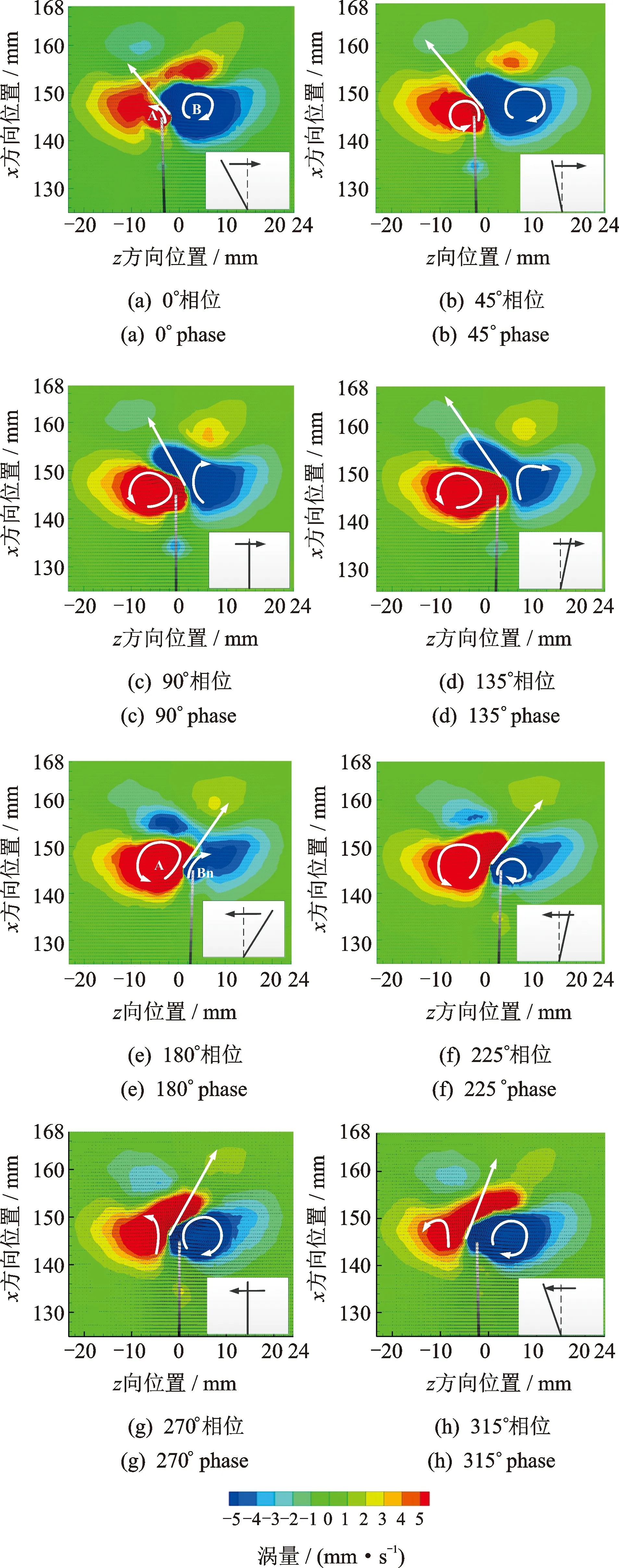
图11 瞬态流场涡量云图以及速度矢量变化图Fig.11 Computed instantaneous velocity fields and vorticity distribution
从摆动的推进器端部涡流发展变化的8幅时间序列图11(a)~(h)中可以看出:推进器端部从左向右的摆动过程中(0→180°),在0→45°相位,推进器端部左侧萌发出一个新的逆时针旋涡A,见图11(a)。随着推进器加速向右摆动,旋涡的强度和范围不断发展壮大,在45°相位已经有了明显的圆环形状见图11(b),且旋涡的面积和能量密度逐渐增大(45°→90°→135°),直到推进器摆动到右极限位置相位180°,左侧逆时针旋涡A与推进器末端完全脱离,见图11(e)。而同时,在推进器末端右侧又酝酿出一个新生的顺时针旋涡Bn (图11e),在推进器末端从右向左的摆动过程中(180→270°→0°+T),顺时针旋涡Bn不断形成、壮大、直至最后脱落。在顺时针旋涡Bn发展的同时,逆时针旋涡A完全脱离推进器末端向右后传播,且能量强度逐渐减小(图11(a),(f)~(h))。
从图11涡流云图的变化过程中可以看出:由于上一个周期内产生旋涡的存在,在一个摆动周期内的任意相位,推进器端部一对交替出现、旋向相反的旋涡始终清晰可见,并且两个旋向相反的旋涡相遇并卷到一起,形成一对近似对称的涡环结构;在下一个周期里,推进器摆动引起的流场特征和上一个周期相似,从而周而复始产生新的涡流,涡流又周期性地脱落,进而产生“反卡门涡街”流场结构,此种结构在水中生物游动过程中被观察到,并用来解释鱼类生物的游动推进机理[15-16]。
由于反卡门涡街结构的存在,两个旋向相反的旋涡交汇在一起,产生一股向斜后方运动的射流,如图11(a)~(h)中的白色直线所示。推进器结构在射流反作用力的作用下向前推进。这就是推进器模拟鱼类游动的摆动式推进机理。
4.2 CFD推进力计算
图12给出了推进器端部沿x方向上的推进力随时间变化曲线。由图可知,由于推进器端部刚开始启动阶段加速度比较大,推进力明显增大;在周围流体阻力作用下,波动曲线幅值开始衰减,在2 s之后趋于稳定。由于推进力的波动曲线不是关于x轴对称的,因此推进力一个周期内的平均值不等于零,故能给推进器提供动力。仿真结果表明,在摆动频率为4 Hz,单侧摆幅达到5.2 mm条件下,推进器端部在x方向上的平均推进力可达到1.5 mN。
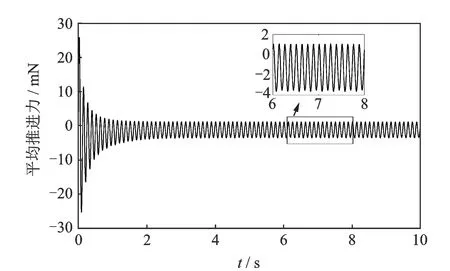
图12 推进器端部x方向上的推进力时变曲线Fig.12 Variation of the thrust at the x direction
5 结束语
借鉴鲹科鱼类的推进方式和游动特点,笔者提出了一种宏压电纤维致动的仿鲹科谐振式水下推进器。仿生推进器性能测试实验结果表明:空气中仿生推进器在固有频率处具有最佳摆动效果,摆幅最大;而在周围流体作用下,仿生推进器在水下的固有频率和最大摆幅都远小于空气中的情况,且其最大摆幅在略微小于水下固有频率处取得,随着驱动电压幅值的升高,存在着刚度软化现象。
采用CFD分析了仿生推进器在稳定摆动过程中不同相位的流场特性和尾迹旋涡的分布情况。从推进器瞬态流场的涡量云图中观察到了“反卡门涡街”结构,且在两个旋涡的交汇地带产生了一股向斜后运动的水流,推进器在向后喷射水流的反作用力下向前推进。故揭示了仿生推进器的流体动力学机制和推进机理。数值计算结果表明,推进器端部在x方向上的平均推进力可达到1.5 mN。笔者的研究结果对智能材料驱动的水下推进器的设计和推进机理研究具有一定的参考和借鉴意义。
