海上风机基础灌浆连接段轴心受压承载力数值分析

2020-12-04张持海曹城城

同济大学学报（自然科学版） 2020年10期

陈涛，张持海，王衔，曹城城

（1. 同济大学工程结构服役性能演化与控制教育部重点实验室，上海200092；2. 同济大学土木工程学院，上海200092）

灌浆连接段广泛应用于海上风机基础支撑结构中，通过对套管和桩管之间的环形空间灌浆，可以使上部结构和下部桩基础形成一个整体。上部结构的荷载可以通过灌浆连接段传到下部基础。因此，灌浆连接段在海上风机支撑结构中发挥着至关重要的作用。

灌浆连接段最早应用在海上石油开采平台的导管架基础中，国内外学者对此类灌浆连接段在轴向荷载下的受力性能开展了大量的试验研究。Billington等［1］对灌浆连接段轴心受压承载力的影响因素开展了试验研究，并对试验结果进行了统计回归，提出了灌浆连接段轴心受压承载力的计算公式。研究发现影响灌浆连接段轴心受压承载力与灌浆连接段的径向刚度、长径比、剪力键的几何尺寸、钢管表面粗糙程度、灌浆料的受压强度等有关。Aritenang等［2］研究了带剪力键灌浆连接段在轴力作用下的破坏机理，并认为灌浆连接段的破坏与桩管的环向屈服有关。Lamport 等［3］设计试验研究了偏心弯矩作用对灌浆连接段轴心受压承载力的影响。Krahl 等［4］基于试验观察到的结果，提出了灌浆连接段斜压短柱分析模型。韩瑞龙等［5］对灌浆套筒的受力性能开展了试验研究，发现灌浆节点所观测到的极限承载力可以达到设计承载力的10 倍以上，设计过于保守。王震等［6］对预应力灌浆套筒的受力性能开展了试验研究。

近年来灌浆连接段开始应用于海上风机结构。由于海上风电的快速发展，灌浆连接段的工程应用呈现出新的特点：①剪力键布置形式的改变。在之前的灌浆连接段设计中，剪力键是沿着连接段全长布置。为了改善灌浆连接段的抗疲劳性能，现行DNV（DET NORSKE VERITAS）规范要求剪力键布置在灌浆连接段的1/2区域［7］。②高强灌浆料的应用。以往的灌浆连接段缩尺试验采用的灌浆料强度值的范围在10～50 MPa。而随着材料科学的发展，目前在海上风电工程中所采用的灌浆料强度均在80 MPa 以上［8］。Schaumann等［9］和Anders等［10］的试验表明，高强度灌浆材料可以显著提高灌浆连接段的受力性能。③大直径化的趋势。目前，海上风机单桩基础灌浆连接段的直径存在持续增加的趋势。直径的增加意味着桩管和套管对于灌浆料的约束效应持续降低［11］。Prakhya等［12］和Marion等［13］利用有限元分析的方法证明了大直径的灌浆连接段应力状态与小直径灌浆连接段不同，对大直径灌浆连接段进行进一步分析是非常必要的。李炜等［14］通过对灌浆连接段进行轴向承载力试验，证明了现有设计规范存在的不足。过去小尺寸的灌浆连接段试验结果对于当下的工程实践不再适用。因此，有必要对应用在海上风电工程中的灌浆连接段开展深入研究。

有限元方法作为一种在工程界应用广泛的数值分析方法，已成为试验分析方法的重要补充［15］。与试验相比，有限元分析更省时省力，适合进行参数分析。目前已有学者采用有限元方法对灌浆连接段开展了分析。Löhning 等［16采用有限元方法解释了无剪力键灌浆连接段出现滑移破坏的原因。Tziavos等［17］采用有限元分析的方式对灌浆连接段四点弯曲试验进行了数值模拟，结果吻合良好。王振宇等［18］对大直径灌浆连接段局部平板试验模型开展了有限元分析。然而，目前对于轴心受压荷载作用下灌浆连接段影响参数的研究还比较少，因此，有必要对影响灌浆连接段轴心受压受力性能的参数开展进一步研究。本文首先对Jeong‐Hwa学者试验结果［19］进行模拟，以验证本文有限元建模方法的可靠性。随后，对灌浆连接段的轴心受压受力性能展开进一步的参数分析，重点研究了径向刚度、剪力键高距比和长径比3 个因素对于灌浆连接段轴心受压受力性能的影响。

1 灌浆连接段轴压数值模型的建立

1.1 数值模型参数设计

为了对灌浆连接段轴心受压极限承载力进行深入研究，共考虑了3种参数：径向刚度k、剪力键高距比h/s以及长径比Lg/Dp。数值模型参数设计如表1所示。表中，Dp和tp为桩管外径和桩管厚度；DTp和tTp分别为套管外径和套管厚度；tg为灌浆层厚度；Lg为灌浆连接段长度；h 和s 为剪力键的高度和间距。图1给出了灌浆连接段试件尺寸示意图。

DNV规范对于径向刚度k的定义如式（1）所示。该表达式同时考虑了桩管、灌浆层以及套管的径向刚度，并将其量纲一化。

式中：Es、Eg分别为钢材和灌浆料的弹性模量；Dg、Dp分别为灌浆层和桩管的外直径；tg、tp分别为灌浆层和桩管的厚度。

图1 灌浆连接段几何尺寸示意图Fig. 1 Schematic diagram of geometric dimensions of grouted connection

1.2 有限元模型的建立

在本文中，灌浆连接段的有限元模型采用分离式建模，即桩管、套管和灌浆层环状体分开建模［20］。其中，套管（桩管）与灌浆层的相关作用采用软件中的接触定义来进行模拟。为了节省计算时间，考虑到灌浆连接段试件和荷载条件的对称性，有限元模型采用半对称模型。ABAQUS 中建立的有限元模型如图2 所示。图中，dx、dy、dz分别代表x、y、z 方向的位移，rx、ry分别代表绕x、y轴的转角。

表1 灌浆连接段模型几何尺寸参数表Tab. 1 Parameter of geometric dimensions of grouted connection

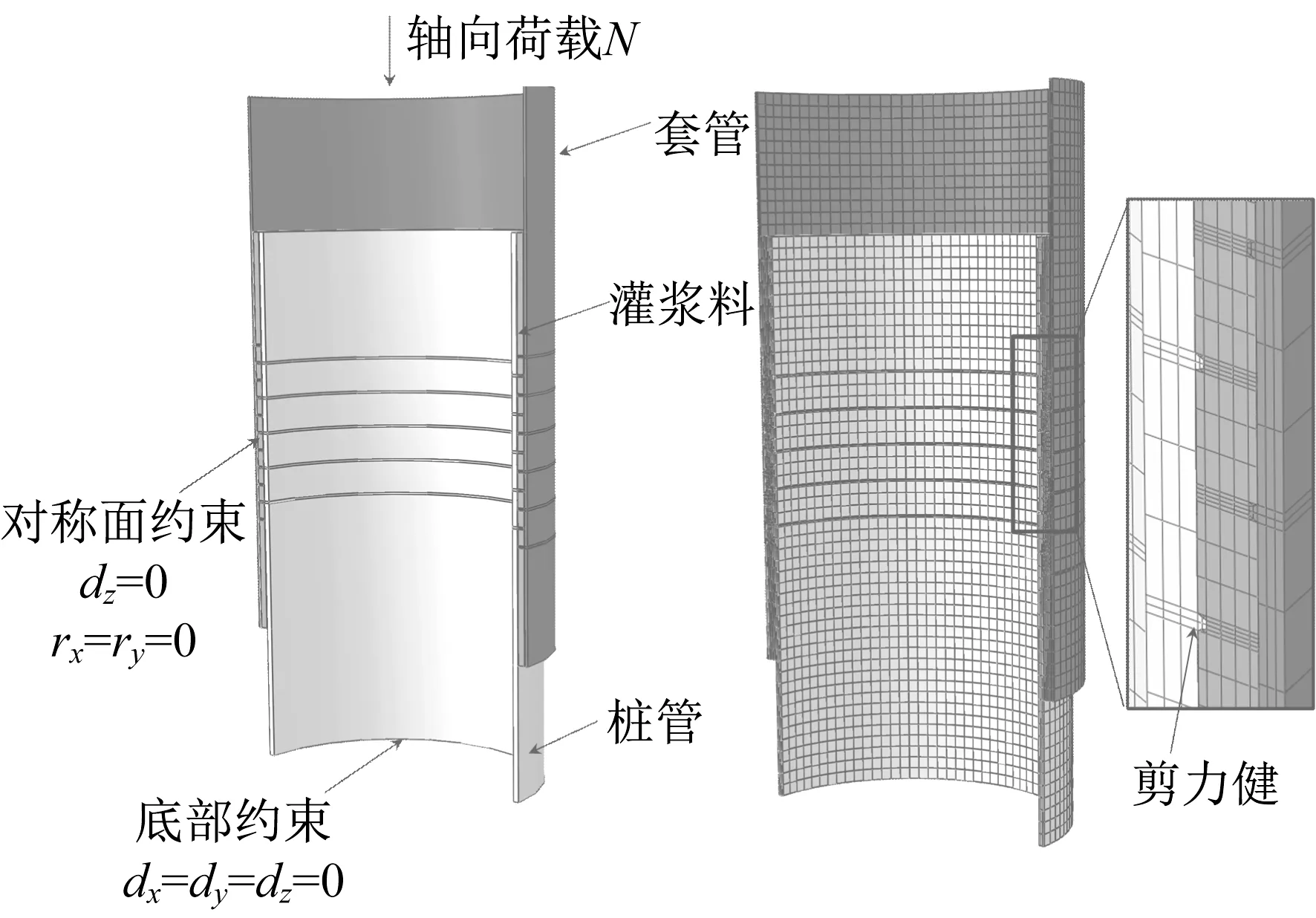
图2 灌浆连接段几何建模及网格划分Fig. 2 Geometric modeling and mesh generation of grouted connection

本次有限元建模采用ABAQUS自带的CDP模型模拟灌浆材料的力学性能。钢材的塑性行为采用随动强化法则和von Mises 屈服准则来进行模拟。钢材的弹性模量Es值取2. 06×105MPa，泊松比为0. 3，屈服强度fy= 360 MPa。灌浆材料弹性模量为Eg=5. 07×104MPa，泊松比为0. 2，抗压强度fc=87. 6 MPa［15］。

钢材与灌浆料之间的法线方向的接触性质采用硬接触（hard contact）定义，模拟套管（桩管）和灌浆材料之间的相互挤压。切线方向的接触性质采用无黏结的库伦摩擦模型定义，模拟套管（桩管）和灌浆材料之间相互错动产生的摩擦力。有限元考虑几何大变形，求解采用Newton‐Raphson法进行。

1.3 有限元模型的验证

为验证本文所提出的有限元数值建模方法的可行性，本文选取了Jeong‐Hwa 学者的灌浆连接段缩尺试验［19］中的两个轴心受压试件CL‐S65 及CL‐S85，进行有限元分析，二者除了剪力键的间距不同，其他的参数均相同。验证模型的材料参数均取自原文试验结果。将有限元分析计算的结果与Jeong‐Hwa学者的试验结果进行对比来证明有限元模型的有效性。Jeong‐Hwa试验的基本情况如图3所示。

试验结果对比主要包括3 个方面：①灌浆连接段试件的最终破坏形态对比；②荷载‐位移关系曲线与极限承载力的对比；③套管纵向应变比较。由于试验对每个试件只测出了4 个点的应变，提取的数值计算结果与试验值差距比较大，在此未进行灌浆材料应变的对比。

1. 3. 1 破坏模式对比

灌浆连接段有限元计算破坏形态和试验破坏形态对比如图4 所示。可以发现，灌浆连接段灌浆层的应力分布出现明显的斜压短柱形态（图中菱形框），这与试验中将灌浆连接段剖开后观察到的灌浆料裂缝分布是一致的。有限元模型在达到极限荷载时在第一对剪力键上方的套管出现屈曲，这也与采用分离式建模的方法有关。

1. 3. 2 荷载‐位移曲线对比

灌浆连接段有限元计算和试验结果的轴心受压荷载‐位移关系曲线如图5所示。该位移为在灌浆连接段端部建立的参考点的位移，用其代表灌浆连接段的轴向位移。比较可得，有限元计算结果与试验结果吻合良好。有限元模型预测试件的峰值承载力与试验相比误差不超过7. 5%。以上误差主要是由于有限元建立的是连续模型，该模型不能反映由于灌浆材料的开裂、压碎等导致的灌浆连接段刚度的变化。还有在试验中的钢管的初始缺陷和制造误差等。以上原因导致试验与模拟结果产生差异。

1. 3. 3 套管纵向应变对比

图3 Jeong⁃Hwa试验简况Fig. 3 Overview of Jeong-Hwa test

图4 破坏模式对比Fig. 4 Comparison of failure modes

灌浆连接段试件CL‐S65和CL‐S85试件的套管纵向应变的有限元计算值与试验结果的比较如图6所示。图中，εy为钢材的屈服应变。观察可知，有限元计算值与试验测量得到的值虽然存在一定的差异，但是总体变化趋势一致。

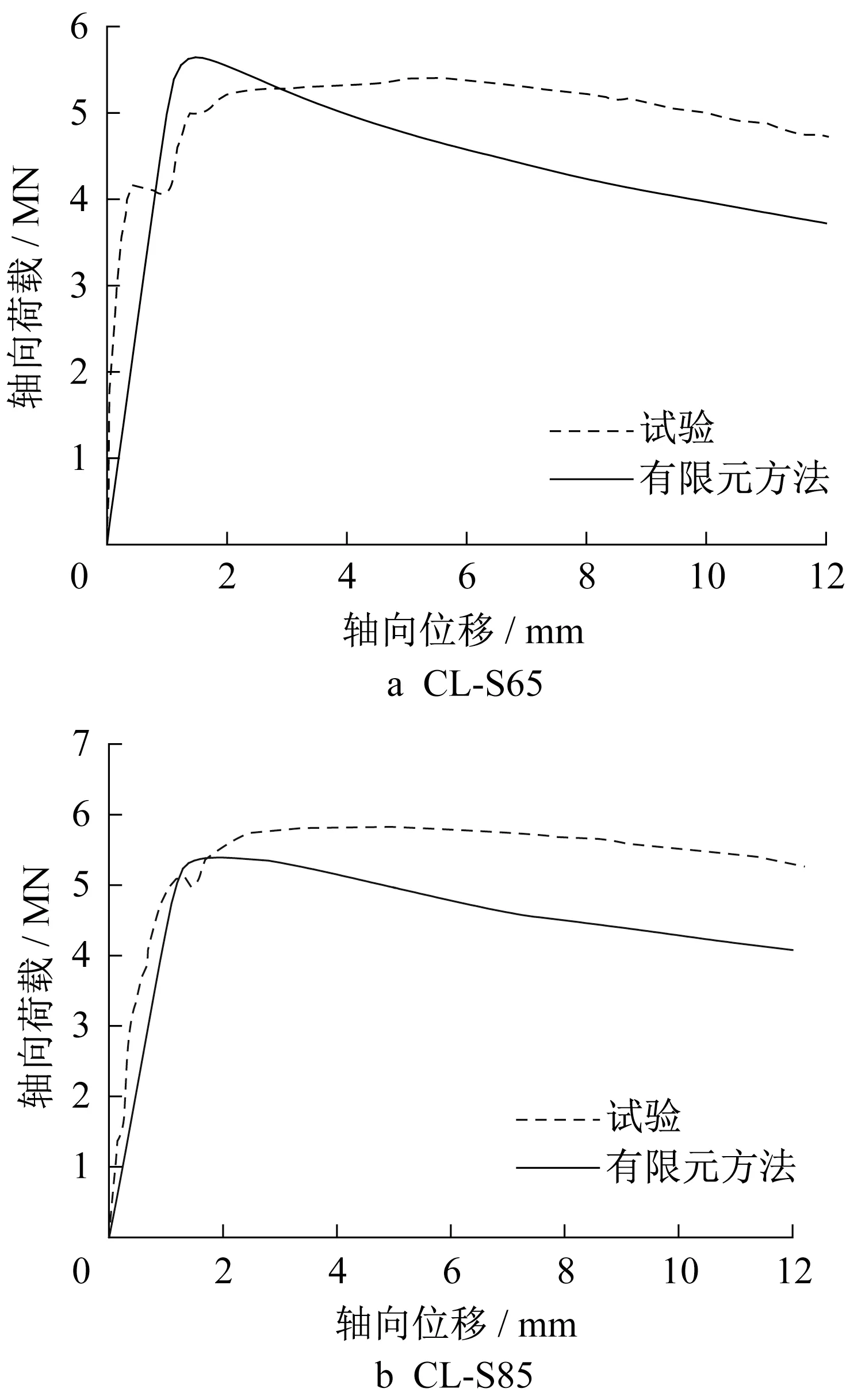
图5 荷载⁃位移曲线对比Fig. 5 Comparison of load-displacement curves

综上所述，从破坏形态、荷载位移曲线以及套管纵向应变3 个方面分析可知，本文所提到的有限元模型计算结果与Jeong‐Hwa试验的测量结果吻合良好。该有限元建模方法能够准确反映灌浆连接段在轴心受压荷载作用下的受力性能，能够用于对灌浆连接段受力性能的深入分析。

2 有限元结果分析

2.1 灌浆体应力状态分析

图6 套管纵向应变对比Fig. 6 Comparison of longitudinal strain of pile

相比于传统的试验测量手段，采用有限元计算方法可以较为全面地获得结构的应力状态分布。现以试件GC‐L‐2为例来说明灌浆连接段内套管与桩管之间的灌浆层的应力状态分布规律。GC‐L‐2试件达到极限承载力时的灌浆材料的应力分布状况如图7所示。

在轴向荷载作用下，灌浆连接段的灌浆层应力较高的部位主要位于套管与桩管的剪力键位置附近。在交错分布的桩管剪力键与套管剪力键之间形成了一个个斜压短柱，通过这些斜压短柱，灌浆连接段将桩管所承受的轴力传递到套管。

随着竖向荷载不断增加，灌浆材料的Tresca应力水平也不断增大。当达到轴心受压极限承载力时，最大Tresca应力点出现在灌浆层底部的外表面第一个剪力键附近，对应的Tresca应力值是180. 5 MPa。可以发现，该Tresca应力值远大于在前处理中定义的灌浆材料的单轴抗压强度。

综上所述，灌浆连接段通过桩管的剪力键和套管的剪力键相互挤压灌浆材料，形成斜向受压短柱并以此传递轴向荷载。根据灌浆材料的应力分布的不均匀性，灌浆材料的破坏只有可能是剪力键位置处的局部压坏。在灌浆料出现局部破碎之后，通过灌浆体内部的应力重分布，未发生破坏的浆体仍能继续支撑套管，灌浆连接段能够继续传递荷载。

图7 灌浆体应力分布Fig. 7 Stress distribution of grout

2.2 轴心荷载⁃位移曲线分析

2. 2. 1 径向刚度的影响

图8给出了径向刚度k对灌浆连接段轴向荷载‐位移曲线的影响。观察4个试件的荷载‐位移曲线可知，曲线均出现了明显的上升段和下降段，灌浆连接段达到轴心受压极限承载力时的破坏模式为套管的屈曲。4 个试件均在竖向位移位于4 mm 左右时达到极限承载力，之后轴心受压承载力不断减小。

灌浆连接段GC‐K‐1～GC‐K‐4试件的极限承载力分别为19 819. 1、20 463. 3、21 690. 3 、22 576. 7 kN。当径向刚度k从0. 010变化到0. 018时，轴心受压极限承载力提升了约14%。

2. 2. 2 剪力键高距比的影响

图9给出了剪力键高距比h/s对荷载‐位移曲线的影响，GC‐H‐1～GC‐H‐4 试件的极限承载力分别为22 387. 3 、21 347. 1、20 731. 6 、19 723. 1 kN。随着剪力键高距比h/s的增加，灌浆连接段的轴心受压极限承载力不断增加。当剪力键高距比从0. 040减小到0. 016时，轴心受压极限承载力降低了约13%。

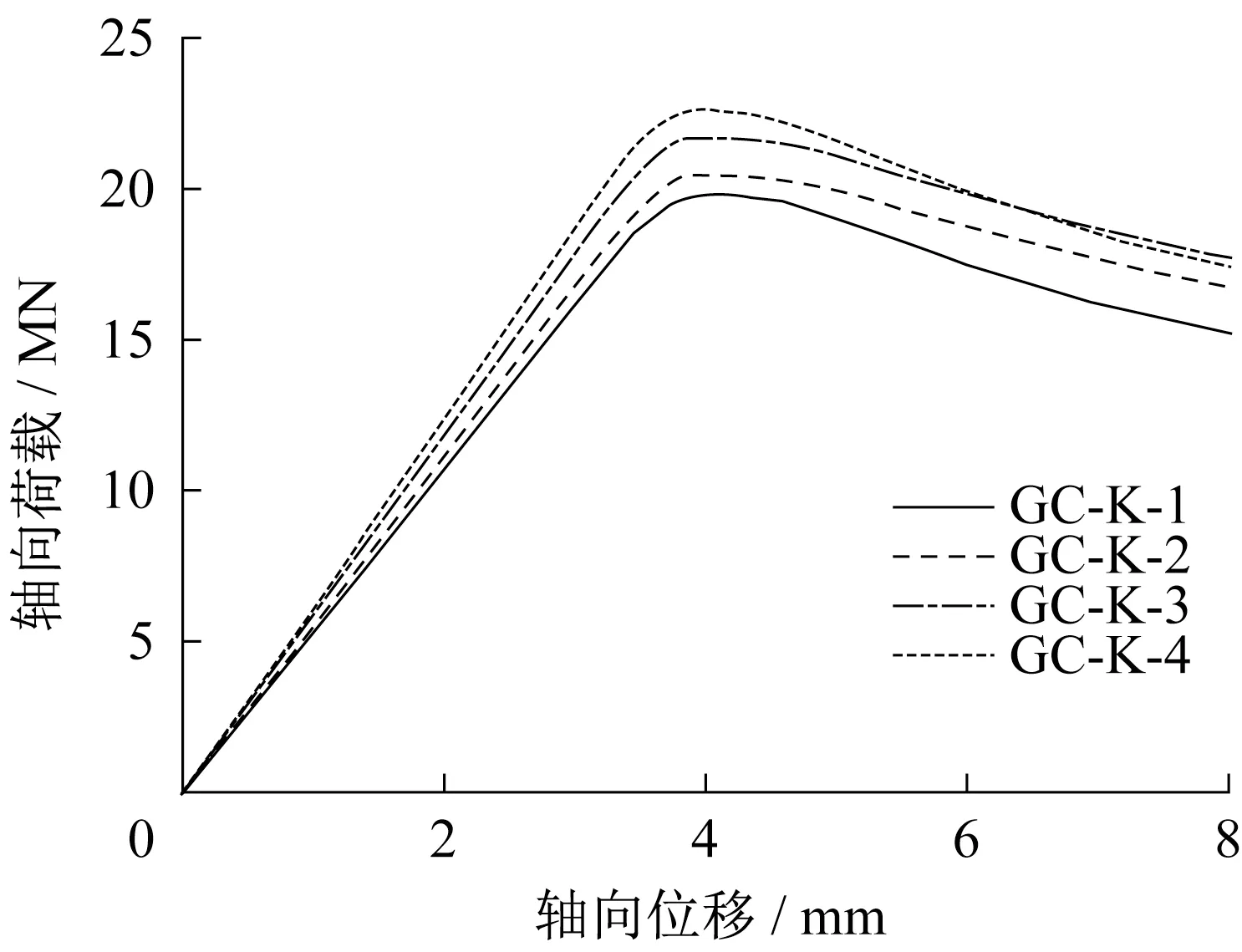
图8 径向刚度对P⁃Δ曲线的影响Fig. 8 Effect of radial stiffness on P⁃Δ curves

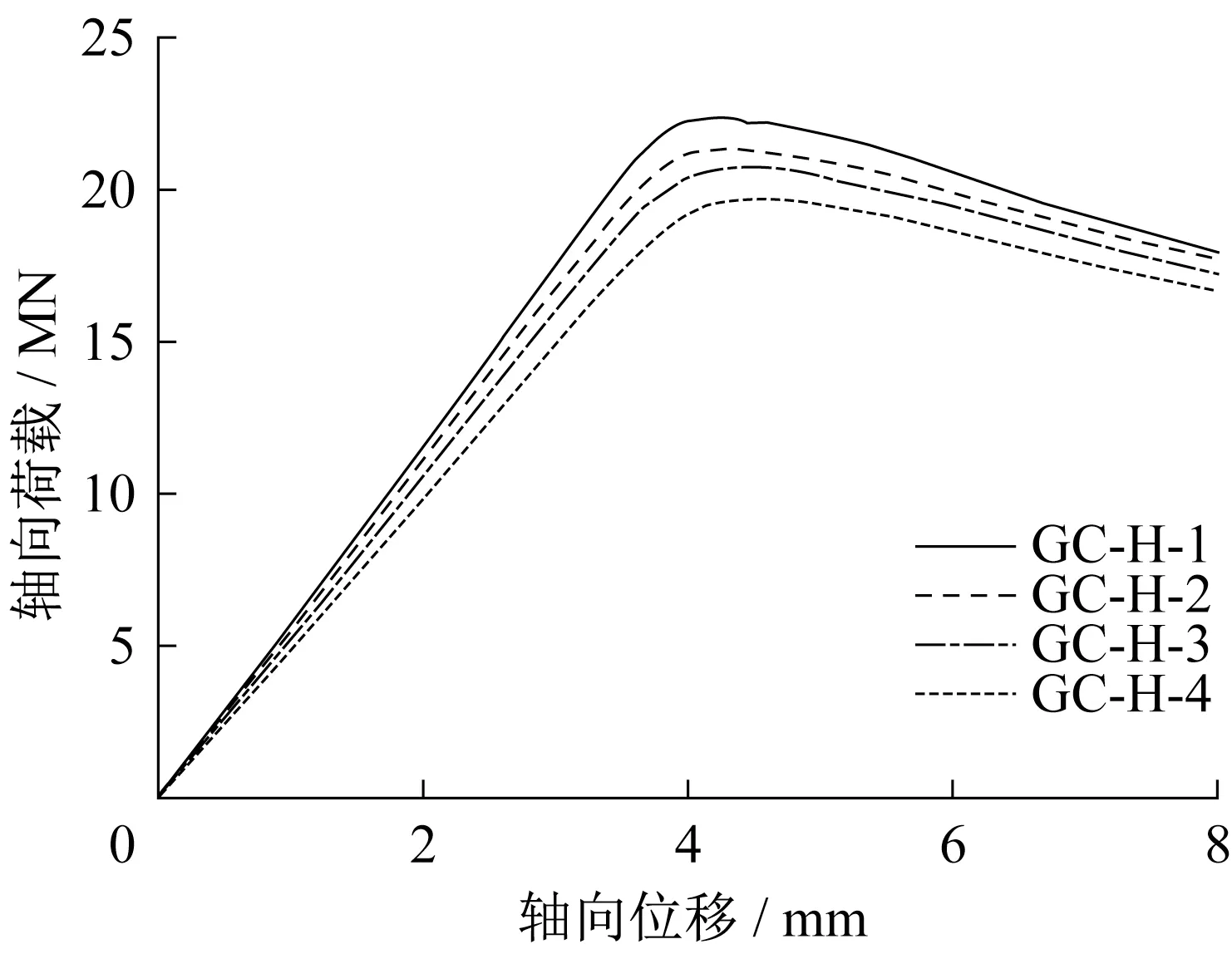
图9 高距比h/s对P⁃Δ曲线的影响Fig. 9 Effect of h/s on P⁃Δ curves

高距比主要通过影响斜压短柱的数量影响灌浆连接段的极限承载力。当高距比不断减小时，即套管与桩管剪力键之间的间距不断增大，从而使得内外剪力键对所形成的斜压短柱的数量不断减小，进而导致灌浆连接段的轴心受压极限承载力不断下降。

2. 2. 3 长径比的影响

图10给出了灌浆连接段的长径比Lg/Dp对荷载‐位移曲线的影响。GC‐L‐1～GC‐L‐4 的极限承载力分别为16 566. 3、17 869. 3、18 907. 4 、19 673. 1 kN。长径比的增加将提升灌浆连接段的轴心受压极限承载力，这是因为长径比的增加一方面增加了灌浆料与套管（桩管）之间的接触面积，从而提升了摩擦力，另一方面长径比的增加也意味着剪力键数量的增加，从而增加了斜压短柱的数量。长径比从1. 0 变化到2. 0 的时候，轴心受压极限承载力提升了约19%。

图10 长径比Lg/Dp对P⁃Δ曲线的影响Fig. 10 Effect of Lg/Dp on P⁃Δ curves

2.3 等效黏结强度与延性分析

由于灌浆连接段独特的几何构造，DNV规范采用等效黏结强度fcu（interface transfer strength）来衡量灌浆连接段的极限承载力。等效界面黏结强度fcu的定义如下：

式中：Pu为灌浆连接段的极限承载力；Lg为灌浆层的长度。

径向刚度k，剪力键高距比h/s和长径比Lg/Dp对于等效黏结强度的影响如表2所示。随着径向刚度k的增加以及高距比h/s的增加，等效界面黏结强度fcu同样也呈现出增加的趋势。但是长径比Lg/Dp对于等效界面黏结强度fcu的影响却有所不同，当长径比从1. 0增加到2. 0的时候，轴心受压极限承载力提升了约19%，而等效界面黏结强度fcu反而降低了69%。因此，通过提升灌浆连接段的长径比来增加灌浆连接段的极限承载力，是一种不经济的做法。

灌浆连接段在轴向荷载作用下的延性采用位移延性系数μΔ进行评估（结果如表2 所示），其定义为极限位移Δu与屈服位移Δy的比值，公式如下：

式中：Δu为灌浆连接段的极限位移；Δy为灌浆连接段的屈服位移。

极限位移Δu是根据《建筑抗震试验规程：JGJ/T 101—2015》中的规定，将峰值荷载之后0. 85Pmax对应的位移定义为结构的极限位移。很难直接从荷载‐位移曲线中直接看出屈服位移，屈服位移Δy根据Park法［21］确定。

分析表2可知，随着灌浆连接段径向刚度k不断增加，灌浆连接段在轴向荷载作用下延性略有改善。当径向刚度从0. 010变化到0. 018时，延性系数μΔ的值提升了25%左右。当高距比从0. 040减小到0. 016时，延性系数μΔ的值提升了约12%。长径比对于灌浆连接段试件延性存在不利影响，当长径比从1. 0增加到2. 0时，试件的延性系数μΔ的值减少了约29%。

表2 数值分析结果汇总Tab. 2 Summary of numerical analysis results

2.4 套管与灌浆料端部接触压力分析

在实际工程设计中，通过控制灌浆连接段端部的接触应力，可以避免端部灌浆料在反复荷载作用下出现破碎。通过提取轴向荷载作用下灌浆连接段端部的接触压力，以期对套管与灌浆料之间的相互作用有一个更加深入的了解。图11a 给出了径向刚度k 对于灌浆连接段端部接触压力的影响。GC‐K‐1～GC‐K‐4灌浆连接段试件的端部接触压力峰值分别为1. 17、1. 38、1. 77、1. 89 MPa。当径向刚度k 从0. 010变化到0. 018的时候，端部峰值接触压力提升了约61%。图11b 给出了剪力键高距比h/s 对于灌浆连接段端部接触压力的影响。GC‐H‐1～GC‐H‐4灌浆连接段试件的端部接触压力峰值分别为1. 05、0. 97、0. 94、1. 09 MPa。因此，剪力键高距比h/s 对于灌浆连接段端部接触压力无显著影响。图11c 给出了长径比Lg/Dp对于灌浆连接段端部接触压力的影响。其端部接触压力峰值分别为1. 43 、1. 17、1. 06、0. 97 MPa。长径比Lg/Dp从1. 0 变化到2. 0，灌浆连接段的端部峰值接触压力降低了约32%。